WikiDer > Kompleks politop
Yilda geometriya, a murakkab politop a ning umumlashtirilishi politop yilda haqiqiy makon a-dagi o'xshash tuzilishga murakkab Hilbert maydoni, bu erda har bir haqiqiy o'lchov an bilan birga keladi xayoliy bitta.
Murakkab politopni murakkab nuqtalar, chiziqlar, tekisliklar va boshqalarning to'plami deb tushunish mumkin, bu erda har bir nuqta bir nechta chiziqlarning birlashishi, bir nechta tekisliklarning har bir chizig'i va boshqalar.
Aniq ta'riflar faqat uchun mavjud muntazam kompleks politoplar, qaysiki konfiguratsiyalar. Muntazam kompleks politoplar to'liq tavsiflangan bo'lib, ular tomonidan ishlab chiqilgan ramziy belgilar yordamida tavsiflanishi mumkin Kokseter.
To'liq muntazam bo'lmagan ba'zi bir murakkab politoplar ham tavsiflangan.
Ta'riflar va kirish
The murakkab chiziq bilan bitta o'lchov mavjud haqiqiy koordinatalari va boshqasi bilan xayoliy koordinatalar. Ikkala o'lchovga ham haqiqiy koordinatalarni qo'llash, haqiqiy sonlarga nisbatan ikki o'lchovni beradi deyiladi. Xayoliy o'qi shunday belgilanadigan haqiqiy tekislik an deb ataladi Argand diagrammasi. Shu sababli uni ba'zan murakkab tekislik deb atashadi. Kompleks 2-bo'shliq (ba'zan ularni murakkab tekislik deb ham atashadi), shuning uchun reellar ustidagi to'rt o'lchovli bo'shliq va hk.
Kompleks n-politop kompleksda n- bo'shliq haqiqiyning analogidir n-politop haqiqatda n- bo'shliq.
Haqiqiy chiziqdagi (yoki tegishli kombinatorial xususiyatlarning) nuqtalarini tartibga solishning tabiiy kompleks analoglari mavjud emas. Shu sababli, murakkab politopni tutashgan sirt sifatida ko'rish mumkin emas va u ichki qismni haqiqiy politop singari bog'lamaydi.
Bo'lgan holatda muntazam simmetriya tushunchasi yordamida aniq ta'rif berish mumkin. Har qanday kishi uchun muntazam politop simmetriya guruhi (bu erda a murakkab aks ettirish guruhideb nomlangan Shephard guruhi) vaqtinchalik harakat qiladi bayroqlar, ya'ni tekislikda joylashgan chiziqda joylashgan nuqtaning ichki ketma-ketliklarida va hokazo.
To'liqroq, to'plam deb ayting P affin subspaces (yoki kvartiralar) kompleks unitar makon V o'lchov n quyidagi shartlarga javob beradigan bo'lsa, muntazam kompleks politop hisoblanadi:[1][2]
- har bir kishi uchun −1 ≤ men < j < k ≤ n, agar F kvartiradir P o'lchov men va H kvartiradir P o'lchov k shu kabi F ⊂ H unda kamida ikkita kvartira bor G yilda P o'lchov j shu kabi F ⊂ G ⊂ H;
- har bir kishi uchun men, j shu kabi −1 ≤ men < j − 2, j ≤ n, agar F ⊂ G ning kvartiralari P o'lchovlar men, j, keyin orasidagi kvartiralar to'plami F va G biriktirilgan ketma-ketlik bilan ushbu to'plamning istalgan a'zosidan boshqasiga o'tishi mumkin degan ma'noda bog'langan; va
- unitar transformatsiyalarning quyi qismi V bu tuzatish P o'tish davri bayroqlar F0 ⊂ F1 ⊂ … ⊂Fn ning kvartiralari P (bilan Fmen o'lchov men Barcha uchun men).
(Bu erda −1 o'lchovli kvartira bo'sh to'plam degan ma'noni anglatadi.) Shunday qilib, ta'rifi bo'yicha muntazam kompleks politoplar konfiguratsiyalar murakkab unitar fazoda.
The muntazam kompleks politoplar tomonidan kashf etilgan Shephard (1952) va nazariyani Kokseter (1974) yanada rivojlantirdi.
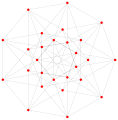
 Ushbu murakkab ko'pburchak 8 qirraga ega (murakkab chiziqlar), deb belgilangan a..hva 16 ta tepalik. Har bir chekkada to'rtta tepalik yotadi va har bir tepada ikkita chekka kesishadi. Chapdagi rasmda belgilangan kvadratchalar politopning elementlari emas, balki xuddi shu murakkab chiziqda yotgan tepaliklarni aniqlashga yordam berish uchun kiritilgan. Chap rasmning sakkiz qirrali perimetri politopning elementi emas, lekin u petri ko'pburchagi.[3] O'rta rasmda har bir chekka haqiqiy chiziq sifatida aks ettirilgan va har bir chiziqdagi to'rtta tepalik aniqroq ko'rinib turadi. |  16 ta vertikal nuqtani katta qora nuqta va 8 ta 4 qirrani har bir chekka ichida chegaralangan kvadrat shaklida ifodalaydigan istiqbolli eskiz. Yashil yo'l chap rasmning sakkizburchak perimetrini aks ettiradi. |
Murakkab politop ekvivalent o'lchovning murakkab maydonida mavjud. Masalan, a murakkab ko'pburchak murakkab tekislikdagi nuqtalardir va qirralar murakkab chiziqlardir samolyotning (afin) pastki bo'shliqlari sifatida mavjud va tepaliklarda kesishgan. Shunday qilib, chekkaga bitta kompleks sondan iborat koordinata tizimi berilishi mumkin.[tushuntirish kerak]
Muntazam kompleks politopda chetga tushgan tepaliklar ularnikiga nosimmetrik tarzda joylashtirilgan centroid, bu ko'pincha chekka koordinata tizimining kelib chiqishi sifatida ishlatiladi (haqiqiy holatda centroid faqat chekkaning o'rta nuqtasidir). Simmetriya a dan kelib chiqadi murakkab aks ettirish centroid haqida; bu aks ettirish qoldiradi kattalik har qanday vertexni o'zgartirmasdan, lekin uni o'zgartiring dalil belgilangan tartibda, uni navbatdagi tepalik koordinatalariga tartibda olib boring. Shunday qilib, biz (mos o'lchov tanlovidan so'ng) chekka tepaliklar tenglamani qondiradi deb taxmin qilishimiz mumkin qayerda p hodisa tepalari soni. Shunday qilib, chekkaning Argand diagrammasida tepalik nuqtalari a ning tepalarida yotadi muntazam ko'pburchak kelib chiqishi markazida.
Muntazam kompleks ko'pburchak 4 {4} 2 ning uchta haqiqiy proektsiyasi yuqorida, qirralar bilan tasvirlangan a, b, c, d, e, f, g, h. Unda 16 ta tepalik bor, ular aniqlik uchun alohida belgilanmagan. Har bir qirrada to'rtta tepalik bor va har bir tepalik ikki qirrada joylashgan, shuning uchun har bir chekka to'rtta boshqa qirraga to'g'ri keladi. Birinchi diagrammada har bir chekka kvadrat bilan tasvirlangan. Maydonning yon tomonlari emas ko'pburchakning qismlari, ammo to'rtta tepalikni vizual ravishda bog'lashga yordam berish uchun faqat chizilgan. Qirralar nosimmetrik tarzda yotqizilgan. (Diagrammaning o'xshashiga e'tibor bering B4 Kokseter tekisligining proektsiyasi ning tesserakt, lekin u tarkibiy jihatdan boshqacha).
O'rta diagramma aniqlik foydasiga sakkiz qirrali simmetriyadan voz kechadi. Har bir chekka haqiqiy chiziq sifatida ko'rsatilgan va ikkita satrning har bir uchrashuv nuqtasi tepalikdir. Turli qirralarning orasidagi bog'lanish aniq ko'rinadi.
Oxirgi diagrammada uch o'lchamga prognoz qilingan tuzilish mazasi berilgan: tepaliklarning ikkita kubigi aslida bir xil o'lchamga ega, ammo to'rtinchi o'lchovda turli masofalarda istiqbolda ko'rinadi.
Muntazam murakkab bir o'lchovli politoplar

Haqiqiy 1 o'lchovli politop haqiqiy chiziqda yopiq segment sifatida mavjud , chiziqdagi ikkita so'nggi nuqta yoki tepalik bilan belgilanadi. Uning Schläfli belgisi bu {}.
Xuddi shunday, kompleks 1-politop ham to'plam sifatida mavjud p murakkab chiziqdagi vertex nuqtalari . Ular an-dagi nuqtalar to'plami sifatida ifodalanishi mumkin Argand diagrammasi (x,y)=x+iy. A muntazam murakkab 1 o'lchovli politop p{} ega p (p ≥ 2) qavariq hosil qilish uchun joylashtirilgan tepalik nuqtalari muntazam ko'pburchak {p} Argand tekisligida.[4]
Haqiqiy chiziqdagi nuqtalardan farqli o'laroq, murakkab chiziqdagi nuqtalar tabiiy tartibga ega emas. Shunday qilib, haqiqiy polytoplardan farqli o'laroq, hech qanday ichki makonni aniqlash mumkin emas.[5] Shunga qaramay, ko'pincha Argand tekisligida chegaralangan muntazam ko'pburchak kabi murakkab 1-politoplar chiziladi.
A muntazam haqiqiy 1 o'lchovli politop bo'sh bilan ifodalanadi Schläfli belgisi {} yoki Kokseter-Dinkin diagrammasi ![]() . Kokseter-Dinkin diagrammasidagi nuqta yoki tugunning o'zi aks ettirish generatorini anglatadi, tugun atrofidagi aylana esa generator nuqtasi aks etmasligini anglatadi, shuning uchun uning aks ettiruvchi qiyofasi o'ziga xos nuqta. Kengaytirilgan holda, muntazam kompleksli 1 o'lchovli politop bor Kokseter-Dinkin diagrammasi
. Kokseter-Dinkin diagrammasidagi nuqta yoki tugunning o'zi aks ettirish generatorini anglatadi, tugun atrofidagi aylana esa generator nuqtasi aks etmasligini anglatadi, shuning uchun uning aks ettiruvchi qiyofasi o'ziga xos nuqta. Kengaytirilgan holda, muntazam kompleksli 1 o'lchovli politop bor Kokseter-Dinkin diagrammasi ![]() , har qanday musbat butun son uchun p, 2 yoki undan katta, o'z ichiga olgan p tepaliklar. p agar u 2. bo'lsa, uni bostirish mumkin. U bo'sh bilan ham ifodalanishi mumkin Schläfli belgisi p{}, }p{, {}p, yoki p{2}1. 1 - mavjud bo'lmagan aks ettirishni ifodalovchi notatsion joylashtiruvchi yoki 1-davr identifikatori. (Haqiqiy yoki murakkab bo'lgan 0-politop nuqta bo'lib,} {, yoki shaklida ifodalanadi 1{2}1.)
, har qanday musbat butun son uchun p, 2 yoki undan katta, o'z ichiga olgan p tepaliklar. p agar u 2. bo'lsa, uni bostirish mumkin. U bo'sh bilan ham ifodalanishi mumkin Schläfli belgisi p{}, }p{, {}p, yoki p{2}1. 1 - mavjud bo'lmagan aks ettirishni ifodalovchi notatsion joylashtiruvchi yoki 1-davr identifikatori. (Haqiqiy yoki murakkab bo'lgan 0-politop nuqta bo'lib,} {, yoki shaklida ifodalanadi 1{2}1.)
Nosimmetriya. Bilan belgilanadi Kokseter diagrammasi ![]() va muqobil ravishda ta'riflanishi mumkin Kokseter yozuvi kabi p[], []p yoki]p[, p[2]1 yoki p[1]p. Simmetriya izomorfik tsiklik guruh, buyurtma p.[6] Ning kichik guruhlari p[] har qanday butun bo'luvchidir d, d[], qaerda d≥2.
va muqobil ravishda ta'riflanishi mumkin Kokseter yozuvi kabi p[], []p yoki]p[, p[2]1 yoki p[1]p. Simmetriya izomorfik tsiklik guruh, buyurtma p.[6] Ning kichik guruhlari p[] har qanday butun bo'luvchidir d, d[], qaerda d≥2.
A unitar operator uchun generator ![]() 2π / ga aylanish sifatida qaraladip radianlar soat yo'nalishi bo'yicha qarshiva a
2π / ga aylanish sifatida qaraladip radianlar soat yo'nalishi bo'yicha qarshiva a ![]() chekka bitta unitar aks ettirishning ketma-ket dasturlari yordamida yaratiladi. Bilan 1-politop uchun unitar aks ettirish generatori p tepaliklar e2πmen/p = cos (2π /p) + men gunoh (2π /p). Qachon p = 2, generator eπmen = –1, a bilan bir xil nuqta aks ettirish haqiqiy tekislikda.
chekka bitta unitar aks ettirishning ketma-ket dasturlari yordamida yaratiladi. Bilan 1-politop uchun unitar aks ettirish generatori p tepaliklar e2πmen/p = cos (2π /p) + men gunoh (2π /p). Qachon p = 2, generator eπmen = –1, a bilan bir xil nuqta aks ettirish haqiqiy tekislikda.
Yuqori murakkab politoplarda 1-politoplar hosil bo'ladi p- qirralar. Ikki chekka odatdagi haqiqiy qirraga o'xshaydi, chunki u ikkita tepalikni o'z ichiga oladi, lekin haqiqiy chiziqda bo'lishi shart emas.
Muntazam murakkab ko'pburchaklar
1-politoplar cheksiz bo'lishi mumkin p, juft prizma ko'pburchaklar bundan mustasno, cheklangan muntazam kompleks ko'pburchaklar p{4}2, 5 qirrali (besh qirrali qirralar) elementlar bilan cheklangan va cheksiz muntazam apeyronlarga 6 qirrali (olti burchakli qirralar) elementlar ham kiradi.
Izohlar
Shephardning o'zgartirilgan Schläfli yozuvi
Shephard dastlab o'zgartirilgan shaklini ishlab chiqdi Schläfli notasi oddiy polipoplar uchun. Bilan chegaralangan ko'pburchak uchun p1- qirralar, a p2- tepalik figurasi va tartibning umumiy simmetriya guruhi sifatida o'rnating g, biz ko'pburchakni quyidagicha belgilaymiz p1(g)p2.
Tepaliklar soni V keyin g/p2 va qirralarning soni E bu g/p1.
Yuqorida tasvirlangan murakkab ko'pburchak sakkiz kvadrat qirraga ega (p1= 4) va o'n oltita tepalik (p2= 2). Shundan kelib chiqib, biz buni ishlab chiqishimiz mumkin g = 32, o'zgartirilgan Schläfli belgisini 4 (32) 2 berib.
Kokseterning o'zgartirilgan Schläfli notasi
Zamonaviy yozuv p1{q}p2 tufayli Kokseter,[7] va guruh nazariyasiga asoslangan. Simmetriya guruhi sifatida uning belgisi p1[q]p2.
Simmetriya guruhi p1[q]p2 2 generator R bilan ifodalanadi1, R2, bu erda: R1p1 = R2p2 = I. Agar q teng, (R2R1)q/2 = (R1R2)q/2. Agar q g'alati, (R2R1)(q-1) / 2R2 = (R1R2)(q-1)/2R1. Qachon q g'alati, p1=p2.
Uchun 4[4]2 R bor14 = R22 = Men, (R2R1)2 = (R1R2)2.
Uchun 3[5]3 R bor13 = R23 = Men, (R2R1)2R2 = (R1R2)2R1.
Kokseter-Dinkin diagrammalari
Kokseter shuningdek foydalanishni umumlashtirdi Kokseter-Dinkin diagrammalari masalan, murakkab ko'pburchakka p{q}r bilan ifodalanadi ![]()
![]()
![]() va unga teng keladigan simmetriya guruhi, p[q]r, halqasiz diagramma
va unga teng keladigan simmetriya guruhi, p[q]r, halqasiz diagramma ![]()
![]()
![]() . Tugunlar p va r ishlab chiqaradigan nometallni ifodalaydi p va r tekislikdagi tasvirlar. Diagrammadagi yorliqsiz tugunlarda 2 ta yorliq mavjud. Masalan, haqiqiy muntazam ko'pburchak bu 2{q}2 yoki {q} yoki
. Tugunlar p va r ishlab chiqaradigan nometallni ifodalaydi p va r tekislikdagi tasvirlar. Diagrammadagi yorliqsiz tugunlarda 2 ta yorliq mavjud. Masalan, haqiqiy muntazam ko'pburchak bu 2{q}2 yoki {q} yoki ![]()
![]()
![]() .
.
Bitta cheklov, g'alati filial buyurtmalari bilan bog'langan tugunlar bir xil tugun buyurtmalariga ega bo'lishi kerak. Agar ular bajarilmasa, guruh "yulduzli" ko'pburchaklarni yaratadi, elementlari bir-biri bilan qoplanadi. Shunday qilib ![]()
![]()
![]() va
va ![]()
![]()
![]() oddiy, ammo
oddiy, ammo ![]()
![]()
![]() yulduzli.
yulduzli.
12 qisqartirilmaydigan Shephard guruhlari

p[2q]2 --> p[q]p, indeks 2.
p[4]q --> p[q]p, indeks q.
Kokseter bu muntazam kompleks ko'pburchaklar ro'yxatini sanab o'tdi . Muntazam murakkab ko'pburchak, p{q}r yoki ![]()
![]()
![]() , bor p- qirralar va r-gonal tepalik raqamlari. p{q}r cheklangan politop, agar (p+r)q>pr(q-2).
, bor p- qirralar va r-gonal tepalik raqamlari. p{q}r cheklangan politop, agar (p+r)q>pr(q-2).
Uning simmetriyasi quyidagicha yozilgan p[q]rdeb nomlangan Shephard guruhi, a ga o'xshash Kokseter guruhi, shuningdek, ruxsat berish unitar aks ettirishlar.
Yulduz bo'lmagan guruhlar uchun guruhning tartibi p[q]r sifatida hisoblash mumkin .[9]
The Kokseter raqami uchun p[q]r bu , shuning uchun guruh tartibini quyidagicha hisoblash mumkin . Ortogonal proyeksiyada muntazam kompleks ko'pburchak chizish mumkin h-gonal simmetriya.
Murakkab ko'pburchaklarni hosil qiluvchi ikkinchi darajali echimlar:
| Guruh | G3= G (q,1,1) | G2= G (p,1,2) | G4 | G6 | G5 | G8 | G14 | G9 | G10 | G20 | G16 | G21 | G17 | G18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2[q]2, q=3,4... | p[4]2, p=2,3... | 3[3]3 | 3[6]2 | 3[4]3 | 4[3]4 | 3[8]2 | 4[6]2 | 4[4]3 | 3[5]3 | 5[3]5 | 3[10]2 | 5[6]2 | 5[4]3 | |
| Buyurtma | 2q | 2p2 | 24 | 48 | 72 | 96 | 144 | 192 | 288 | 360 | 600 | 720 | 1200 | 1800 |
| h | q | 2p | 6 | 12 | 24 | 30 | 60 | |||||||
Toqli bo'lgan echimlar q va tengsiz p va r ular: 6[3]2, 6[3]3, 9[3]3, 12[3]3, ..., 5[5]2, 6[5]2, 8[5]2, 9[5]2, 4[7]2, 9[5]2, 3[9]2va 3[11]2.
Boshqa butun q tengsiz bilan p va r, asosiy domenlari ustma-ust keladigan yulduzli guruhlarni yarating: ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() va
va ![]()
![]()
![]() .
.
Ning ikki tomonlama ko'pburchagi p{q}r bu r{q}p. Shaklning ko'pburchagi p{q}p o'z-o'zini dual. Shakl guruhlari p[2q]2 yarim simmetriyaga ega p[q]p, shuning uchun muntazam ko'pburchak ![]()
![]()
![]()
![]()
![]()
![]() quasiregular bilan bir xil
quasiregular bilan bir xil ![]()
![]()
![]()
![]()
![]() . Xuddi shu tugun buyrug'iga ega bo'lgan muntazam ko'pburchak,
. Xuddi shu tugun buyrug'iga ega bo'lgan muntazam ko'pburchak, ![]()
![]()
![]()
![]()
![]() , bor almashtirilgan qurilish
, bor almashtirilgan qurilish ![]()
![]()
![]()
![]()
![]()
![]() , qo'shni qirralarning ikki xil rang bo'lishiga imkon beradi.[10]
, qo'shni qirralarning ikki xil rang bo'lishiga imkon beradi.[10]
Guruh buyurtmasi, g, tepaliklar va qirralarning umumiy sonini hisoblash uchun ishlatiladi. Bu bo'ladi g/r tepaliklar va g/p qirralar. Qachon p=r, tepaliklar va qirralarning soni teng. Bu holat qachon talab qilinadi q g'alati
Matritsa generatorlari
Guruh p[q]r, ![]()
![]()
![]() , ikkita matritsa bilan ifodalanishi mumkin:[11]
, ikkita matritsa bilan ifodalanishi mumkin:[11]
| Ism | R1 | R2 |
|---|---|---|
| Buyurtma | p | r |
| Matritsa |
Bilan
- k =
- Misollar
|
|
| |||||||||||||||||||||||||||
|
|
|
Muntazam kompleks ko'pburchaklarni sanash
Kokseter muntazam polipoplarning III jadvalidagi murakkab ko'pburchaklarni sanab o'tdi.[12]
| Guruh | Buyurtma | Kokseter raqam | Ko'pburchak | Vertices | Qirralar | Izohlar | ||
|---|---|---|---|---|---|---|---|---|
| G (q, q, 2) 2[q]2 = [q] q = 2,3,4, ... | 2q | q | 2{q}2 | q | q | {} | Haqiqiy muntazam ko'pburchaklar Xuddi shunday Xuddi shunday | |
| Guruh | Buyurtma | Kokseter raqam | Ko'pburchak | Vertices | Qirralar | Izohlar | |||
|---|---|---|---|---|---|---|---|---|---|
| G (p,1,2) p[4]2 p = 2,3,4, ... | 2p2 | 2p | p(2p2)2 | p{4}2 | | p2 | 2p | p{} | bilan bir xil p{}×p{} yoki sifatida namoyish etish p-p duoprizm |
| 2(2p2)p | 2{4}p | 2p | p2 | {} | sifatida namoyish etish p-p duopiramida | ||||
| G (2,1,2) 2[4]2 = [4] | 8 | 4 | 2{4}2 = {4} | 4 | 4 | {} | {} × {} yoki bilan bir xil Haqiqiy kvadrat | ||
| G (3,1,2) 3[4]2 | 18 | 6 | 6(18)2 | 3{4}2 | 9 | 6 | 3{} | bilan bir xil 3{}×3{} yoki sifatida namoyish etish 3-3 duoprizm | |
| 2(18)3 | 2{4}3 | 6 | 9 | {} | sifatida namoyish etish 3-3 duopiramida | ||||
| G (4,1,2) 4[4]2 | 32 | 8 | 8(32)2 | 4{4}2 | 16 | 8 | 4{} | bilan bir xil 4{}×4{} yoki 4-4 duoprizm yoki sifatida ifodalanishi {4,3,3} | |
| 2(32)4 | 2{4}4 | 8 | 16 | {} | 4-4 duopiramida yoki shaklida {3,3,4} | ||||
| G (5,1,2) 5[4]2 | 50 | 25 | 5(50)2 | 5{4}2 | 25 | 10 | 5{} | bilan bir xil 5{}×5{} yoki sifatida namoyish etish 5-5 duoprizm | |
| 2(50)5 | 2{4}5 | 10 | 25 | {} | sifatida namoyish etish 5-5 duopiramida | ||||
| G (6,1,2) 6[4]2 | 72 | 36 | 6(72)2 | 6{4}2 | 36 | 12 | 6{} | bilan bir xil 6{}×6{} yoki sifatida namoyish etish 6-6 duoprizm | |
| 2(72)6 | 2{4}6 | 12 | 36 | {} | sifatida namoyish etish 6-6 duopiramida | ||||
| G4= G (1,1,2) 3[3]3 <2,3,3> | 24 | 6 | 3(24)3 | 3{3}3 | 8 | 8 | 3{} | Mobius-Kantor konfiguratsiyasi o'z-o'zini dual, xuddi shunday sifatida namoyish etish {3,3,4} | |
| G6 3[6]2 | 48 | 12 | 3(48)2 | 3{6}2 | 24 | 16 | 3{} | bilan bir xil | |
| 3{3}2 | yulduzli ko'pburchak | ||||||||
| 2(48)3 | 2{6}3 | 16 | 24 | {} | |||||
| 2{3}3 | yulduzli ko'pburchak | ||||||||
| G5 3[4]3 | 72 | 12 | 3(72)3 | 3{4}3 | 24 | 24 | 3{} | o'z-o'zini dual, xuddi shunday sifatida namoyish etish {3,4,3} | |
| G8 4[3]4 | 96 | 12 | 4(96)4 | 4{3}4 | 24 | 24 | 4{} | o'z-o'zini dual, xuddi shunday sifatida namoyish etish {3,4,3} | |
| G14 3[8]2 | 144 | 24 | 3(144)2 | 3{8}2 | 72 | 48 | 3{} | bilan bir xil | |
| 3{8/3}2 | yulduzli ko'pburchak, xuddi shunday | ||||||||
| 2(144)3 | 2{8}3 | 48 | 72 | {} | |||||
| 2{8/3}3 | yulduzli ko'pburchak | ||||||||
| G9 4[6]2 | 192 | 24 | 4(192)2 | 4{6}2 | 96 | 48 | 4{} | bilan bir xil | |
| 2(192)4 | 2{6}4 | 48 | 96 | {} | |||||
| 4{3}2 | 96 | 48 | {} | yulduzli ko'pburchak | |||||
| 2{3}4 | 48 | 96 | {} | yulduzli ko'pburchak | |||||
| G10 4[4]3 | 288 | 24 | 4(288)3 | 4{4}3 | 96 | 72 | 4{} | ||
| 12 | 4{8/3}3 | yulduzli ko'pburchak | |||||||
| 24 | 3(288)4 | 3{4}4 | 72 | 96 | 3{} | ||||
| 12 | 3{8/3}4 | yulduzli ko'pburchak | |||||||
| G20 3[5]3 | 360 | 30 | 3(360)3 | 3{5}3 | 120 | 120 | 3{} | o'z-o'zini dual, xuddi shunday sifatida namoyish etish {3,3,5} | |
| 3{5/2}3 | ikki tomonlama, yulduzli ko'pburchak | ||||||||
| G16 5[3]5 | 600 | 30 | 5(600)5 | 5{3}5 | 120 | 120 | 5{} | o'z-o'zini dual, xuddi shunday sifatida namoyish etish {3,3,5} | |
| 10 | 5{5/2}5 | ikki tomonlama, yulduzli ko'pburchak | |||||||
| G21 3[10]2 | 720 | 60 | 3(720)2 | 3{10}2 | 360 | 240 | 3{} | bilan bir xil | |
| 3{5}2 | yulduzli ko'pburchak | ||||||||
| 3{10/3}2 | yulduzli ko'pburchak, xuddi shunday | ||||||||
| 3{5/2}2 | yulduzli ko'pburchak | ||||||||
| 2(720)3 | 2{10}3 | 240 | 360 | {} | |||||
| 2{5}3 | yulduzli ko'pburchak | ||||||||
| 2{10/3}3 | yulduzli ko'pburchak | ||||||||
| 2{5/2}3 | yulduzli ko'pburchak | ||||||||
| G17 5[6]2 | 1200 | 60 | 5(1200)2 | 5{6}2 | 600 | 240 | 5{} | bilan bir xil | |
| 20 | 5{5}2 | yulduzli ko'pburchak | |||||||
| 20 | 5{10/3}2 | yulduzli ko'pburchak | |||||||
| 60 | 5{3}2 | yulduzli ko'pburchak | |||||||
| 60 | 2(1200)5 | 2{6}5 | 240 | 600 | {} | ||||
| 20 | 2{5}5 | yulduzli ko'pburchak | |||||||
| 20 | 2{10/3}5 | yulduzli ko'pburchak | |||||||
| 60 | 2{3}5 | yulduzli ko'pburchak | |||||||
| G18 5[4]3 | 1800 | 60 | 5(1800)3 | 5{4}3 | 600 | 360 | 5{} | ||
| 15 | 5{10/3}3 | yulduzli ko'pburchak | |||||||
| 30 | 5{3}3 | yulduzli ko'pburchak | |||||||
| 30 | 5{5/2}3 | yulduzli ko'pburchak | |||||||
| 60 | 3(1800)5 | 3{4}5 | 360 | 600 | 3{} | ||||
| 15 | 3{10/3}5 | yulduzli ko'pburchak | |||||||
| 30 | 3{3}5 | yulduzli ko'pburchak | |||||||
| 30 | 3{5/2}5 | yulduzli ko'pburchak | |||||||
Muntazam murakkab ko'pburchaklarning ingl
Shaklning ko'pburchaklari p{2r}q tomonidan ingl q rang to'plamlari p- chekka. Har biri p-dge oddiy ko'pburchak sifatida qaraladi, yuzlar yo'q.
- Murakkab ko'pburchaklarning 2D ortogonal proektsiyalari 2{r}q
Shaklning ko'pburchaklari 2{4}q umumlashtirilgan deyiladi ortoplekslar. Ular tepaliklarni 4D bilan bo'lishadilar q-q duopiramidalar, 2 qirralar bilan bog'langan tepaliklar.
2{4}3,


 , 6 tepalik va 9 chekka bilan[13]
, 6 tepalik va 9 chekka bilan[13]
- Murakkab ko'pburchaklar p{4}2
Shaklning ko'pburchaklari p{4}2 umumlashtirilgan deyiladi giperkubiklar (ko'pburchaklar uchun kvadratchalar). Ular tepaliklarni 4D bilan bo'lishadilar p-p duoprizmalar, p qirralari bilan bog'langan tepaliklar. Vertices yashil rangga chizilgan va pqirralar muqobil ranglarda, qizil va ko'k ranglarda chizilgan. Tepaliklarni markazdan siljitish uchun g'alati o'lchovlar uchun nuqtai nazar biroz buzilgan.
3{4}2,


 yoki
yoki 

 , 9 ta tepalik va 6 ta (uchburchak) 3 qirrali[14]
, 9 ta tepalik va 6 ta (uchburchak) 3 qirrali[14]
- 3D istiqbol murakkab ko'pburchaklarning proektsiyalari p{4}2. Ikkilik 2{4}p
- qirralarning ichiga tepaliklarni qo'shish va tepaliklar o'rniga qirralarni qo'shish orqali ko'rinadi.
- Boshqa murakkab ko'pburchaklar p{r}2
3{6}2,


 yoki
yoki 

 , 24 ta vertikal qora rangda va 16 ta 3 qirralar qizil va ko'k ranglarda 3 qirralarning 2 to'plamida ranglangan[15]
, 24 ta vertikal qora rangda va 16 ta 3 qirralar qizil va ko'k ranglarda 3 qirralarning 2 to'plamida ranglangan[15]3{8}2,


 yoki
yoki 

 , 72 ta vertikallar qora rangda va 48 ta 3 qirralar qizil va ko'k ranglarda 3 qirralarning 2 to'plamida ranglangan[16]
, 72 ta vertikallar qora rangda va 48 ta 3 qirralar qizil va ko'k ranglarda 3 qirralarning 2 to'plamida ranglangan[16]
- Murakkab ko'pburchaklarning 2D ortogonal proektsiyalari, p{r}p
Shaklning ko'pburchaklari p{r}p tepaliklar va qirralarning teng soniga ega. Ular, shuningdek, o'z-o'zini dual.
3{4}3,


 yoki
yoki 

 , 24 ta tepalik va 24 ta 3 qirralarning uchta to'plamida ko'rsatilgan, bitta to'plam to'ldirilgan[18]
, 24 ta tepalik va 24 ta 3 qirralarning uchta to'plamida ko'rsatilgan, bitta to'plam to'ldirilgan[18]4{3}4,


 yoki
yoki 

 , 24 ta tepalik va 24 ta 4 qirralar bilan 4 ta rang to'plamida ko'rsatilgan[19]
, 24 ta tepalik va 24 ta 4 qirralar bilan 4 ta rang to'plamida ko'rsatilgan[19]3{5}3,


 yoki
yoki 

 , 120 ta tepalik va 120 ta 3 qirrali[20]
, 120 ta tepalik va 120 ta 3 qirrali[20]5{3}5,


 yoki
yoki 

 , 120 ta tepalik va 120 ta 5 qirrali[21]
, 120 ta tepalik va 120 ta 5 qirrali[21]
Muntazam kompleks politoplar
Umuman olganda, a muntazam kompleks politop sifatida Kokseter tomonidan ifodalanadi p{z1}q{z2}r{z3}s… Yoki Kokseter diagrammasi ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …, Simmetriyaga ega p[z1]q[z2]r[z3]s… Yoki
…, Simmetriyaga ega p[z1]q[z2]r[z3]s… Yoki ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ….[22]
….[22]
Umumlashtiruvchi har xil o'lchovlarda yuzaga keladigan muntazam kompleks politoplarning cheksiz oilalari mavjud giperkubiklar va o'zaro faoliyat politoplar haqiqiy makonda. Shephardning "umumiy ortotopi" giperkubani umumlashtiradi; uning γ belgisi berilganp
n = p{4}2{3}2…2{3}2 va diagramma ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…![]()
![]()
![]()
![]()
![]() . Uning simmetriya guruhida diagramma mavjud p[4]2[3]2…2[3]2; Shephard-Todd tasnifida bu G guruhidir (p, 1, n) imzolangan almashtirish matritsalarini umumlashtirish. Uning ikki tomonlama muntazam politopi - "umumlashtirilgan o'zaro faoliyat politop" β belgisi bilan ifodalanadip
. Uning simmetriya guruhida diagramma mavjud p[4]2[3]2…2[3]2; Shephard-Todd tasnifida bu G guruhidir (p, 1, n) imzolangan almashtirish matritsalarini umumlashtirish. Uning ikki tomonlama muntazam politopi - "umumlashtirilgan o'zaro faoliyat politop" β belgisi bilan ifodalanadip
n = 2{3}2{3}2…2{4}p va diagramma ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…![]()
![]()
![]()
![]() .[23]
.[23]
1 o'lchovli muntazam kompleks politop yilda sifatida ifodalanadi ![]() ega bo'lish p tepaliklar, uning haqiqiy vakili bilan a muntazam ko'pburchak, {p}. Kokseter shuningdek unga symbol belgisini beradip
ega bo'lish p tepaliklar, uning haqiqiy vakili bilan a muntazam ko'pburchak, {p}. Kokseter shuningdek unga symbol belgisini beradip
1 yoki βp
1 1 o'lchovli umumlashtirilgan giperkubik yoki o'zaro faoliyat politop sifatida. Uning simmetriyasi p[] yoki ![]() , tartibning tsiklik guruhi p. Yuqori politopda, p{} yoki
, tartibning tsiklik guruhi p. Yuqori politopda, p{} yoki ![]() ifodalaydi p-edge elementi, ikki qirrali, {} yoki
ifodalaydi p-edge elementi, ikki qirrali, {} yoki ![]() , ikkita tepalik orasidagi oddiy haqiqiy qirrani ifodalaydi.[24]
, ikkita tepalik orasidagi oddiy haqiqiy qirrani ifodalaydi.[24]
A dual kompleks politop almashtirish orqali quriladi k va (n-1-k) elementlari n-politop. Masalan, ikkitomonlama murakkab ko'pburchakning har bir chekkasida markazlari joylashgan bo'lib, yangi qirralari eski tepalarida joylashgan. A v-valans vertexi yangisini yaratadi v- chekka va e- qirralar bo'ladi e-valans tepalari.[25] Doimiy kompleks politopning duali teskari belgiga ega. Nosimmetrik belgilarga ega bo'lgan muntazam murakkab polytoplar, ya'ni. p{q}p, p{q}r{q}p, p{q}r{s}r{q}pva boshqalar o'z-o'zini dual.
Muntazam murakkab ko'pburchaklarni sanash
Kokseter bu yulduzsiz muntazam kompleks poliedraning ro'yxatini sanab o'tdi , shu jumladan 5 platonik qattiq moddalar yilda .[26]
Muntazam murakkab ko'pburchak, p{n1}q{n2}r yoki ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , bor
, bor ![]()
![]()
![]()
![]()
![]()
![]() yuzlar,
yuzlar, ![]() qirralar va
qirralar va ![]()
![]()
![]()
![]()
![]()
![]() tepalik raqamlari.
tepalik raqamlari.
Murakkab muntazam ko'pburchak p{n1}q{n2}r ikkalasini ham talab qiladi g1 = buyurtma (p[n1]q) va g2 = buyurtma (q[n2]r) cheklangan bo'ling.
Berilgan g = buyurtma (p[n1]q[n2]r), tepalar soni g/g2va yuzlar soni g/g1. Qirralarning soni g/pr.
| Bo'shliq | Guruh | Buyurtma | Kokseter raqami | Ko'pburchak | Vertices | Qirralar | Yuzlar | Tepalik shakl | Van Oss ko'pburchak | Izohlar | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,3) 2[3]2[3]2 = [3,3] | 24 | 4 | a3 = 2{3}2{3}2 = {3,3} | 4 | 6 | {} | 4 | {3} | {3} | yo'q | Haqiqiy tetraedr Xuddi shunday | ||
| G23 2[3]2[5]2 = [3,5] | 120 | 10 | 2{3}2{5}2 = {3,5} | 12 | 30 | {} | 20 | {3} | {5} | yo'q | Haqiqiy ikosaedr | ||
| 2{5}2{3}2 = {5,3} | 20 | 30 | {} | 12 | {5} | {3} | yo'q | Haqiqiy dodekaedr | |||||
| G (2,1,3) 2[3]2[4]2 = [3,4] | 48 | 6 | β2 3 = β3 = {3,4} | 6 | 12 | {} | 8 | {3} | {4} | {4} | Haqiqiy oktaedr {} + {} + {} Bilan bir xil, 8-buyurtma Xuddi shunday | ||
| γ2 3 = γ3 = {4,3} | 8 | 12 | {} | 6 | {4} | {3} | yo'q | Haqiqiy kub {} × {} × {} yoki bilan bir xil | |||||
| G (p, 1,3) 2[3]2[4]p p = 2,3,4, ... | 6p3 | 3p | βp 3 = 2{3}2{4}p | | 3p | 3p2 | {} | p3 | {3} | 2{4}p | 2{4}p | Umumlashtirilgan oktaedr Xuddi shunday p{}+p{}+p{}, buyurtma p3 Xuddi shunday | |
| γp 3 = p{4}2{3}2 | p3 | 3p2 | p{} | 3p | p{4}2 | {3} | yo'q | Umumiy kub Xuddi shunday p{}×p{}×p{} yoki | |||||
| G (3,1,3) 2[3]2[4]3 | 162 | 9 | β3 3 = 2{3}2{4}3 | 9 | 27 | {} | 27 | {3} | 2{4}3 | 2{4}3 | Xuddi shunday 3{}+3{}+3{}, 27-buyurtma Xuddi shunday | ||
| γ3 3 = 3{4}2{3}2 | 27 | 27 | 3{} | 9 | 3{4}2 | {3} | yo'q | Xuddi shunday 3{}×3{}×3{} yoki | |||||
| G (4,1,3) 2[3]2[4]4 | 384 | 12 | β4 3 = 2{3}2{4}4 | 12 | 48 | {} | 64 | {3} | 2{4}4 | 2{4}4 | Xuddi shunday 4{}+4{}+4{}, buyurtma 64 Xuddi shunday | ||
| γ4 3 = 4{4}2{3}2 | 64 | 48 | 4{} | 12 | 4{4}2 | {3} | yo'q | Xuddi shunday 4{}×4{}×4{} yoki | |||||
| G (5,1,3) 2[3]2[4]5 | 750 | 15 | β5 3 = 2{3}2{4}5 | 15 | 75 | {} | 125 | {3} | 2{4}5 | 2{4}5 | Xuddi shunday 5{}+5{}+5{}, buyurtma 125 Xuddi shunday | ||
| γ5 3 = 5{4}2{3}2 | 125 | 75 | 5{} | 15 | 5{4}2 | {3} | yo'q | Xuddi shunday 5{}×5{}×5{} yoki | |||||
| G (6,1,3) 2[3]2[4]6 | 1296 | 18 | β6 3 = 2{3}2{4}6 | 36 | 108 | {} | 216 | {3} | 2{4}6 | 2{4}6 | Xuddi shunday 6{}+6{}+6{}, buyurtma 216 Xuddi shunday | ||
| γ6 3 = 6{4}2{3}2 | 216 | 108 | 6{} | 18 | 6{4}2 | {3} | yo'q | Xuddi shunday 6{}×6{}×6{} yoki | |||||
| G25 3[3]3[3]3 | 648 | 9 | 3{3}3{3}3 | 27 | 72 | 3{} | 27 | 3{3}3 | 3{3}3 | 3{4}2 | Xuddi shunday sifatida namoyish etish 221 Gessian poliedrasi | ||
| G26 2[4]3[3]3 | 1296 | 18 | 2{4}3{3}3 | 54 | 216 | {} | 72 | 2{4}3 | 3{3}3 | {6} | |||
| 3{3}3{4}2 | 72 | 216 | 3{} | 54 | 3{3}3 | 3{4}2 | 3{4}3 | Xuddi shunday sifatida namoyish etish 122 | |||||
Muntazam murakkab poliedraning vizualizatsiyalari
- Murakkab poliedraning 2D ortogonal proektsiyalari, p{s}t{r}r
Haqiqiy {3,3},




 yoki
yoki 



 4 ta tepalikka, 6 ta qirraga va 4 ta yuzga ega
4 ta tepalikka, 6 ta qirraga va 4 ta yuzga ega2{4}3{3}3,




 54 ta tepalikka, 216 ta oddiy qirralarga va 72 ta yuzga ega bo'lib, bitta yuzi ko'k rang bilan ta'kidlangan.[29]
54 ta tepalikka, 216 ta oddiy qirralarga va 72 ta yuzga ega bo'lib, bitta yuzi ko'k rang bilan ta'kidlangan.[29]
- Umumiy oktaedra
Umumiy oktaedra odatdagidek tuzilishga ega ![]()
![]()
![]()
![]()
![]() va quasiregular shakli kabi
va quasiregular shakli kabi ![]()
![]()
![]()
![]() . Barcha elementlar simplekslar.
. Barcha elementlar simplekslar.
Haqiqiy {3,4},




 yoki
yoki 

 , 6 tepalik, 12 chekka va 8 yuz bilan
, 6 tepalik, 12 chekka va 8 yuz bilan
- Umumiy kublar
Umumiy kublar odatiy tuzilishga ega ![]()
![]()
![]()
![]()
![]() va kabi prizmatik qurilish
va kabi prizmatik qurilish ![]()
![]()
![]()
![]()
![]() , uchta mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
, uchta mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
Haqiqiy {4,3},




 yoki
yoki 



 8 tepalik, 12 chekka va 6 yuzga ega
8 tepalik, 12 chekka va 6 yuzga ega3{4}2{3}2,




 yoki
yoki 



 27 tepalik, 27 3 qirrali va 9 yuzga ega[31]
27 tepalik, 27 3 qirrali va 9 yuzga ega[31]
Muntazam kompleks 4-politoplarni sanab chiqish
Kokseter ushbu yulduzsiz oddiy kompleks 4-politoplar ro'yxatini sanab o'tdi , shu jumladan 6 qavariq muntazam 4-politoplar yilda .[32]
| Bo'shliq | Guruh | Buyurtma | Kokseter raqam | Polytope | Vertices | Qirralar | Yuzlar | Hujayralar | Van Oss ko'pburchak | Izohlar |
|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,4) 2[3]2[3]2[3]2 = [3,3,3] | 120 | 5 | a4 = 2{3}2{3}2{3}2 = {3,3,3} | 5 | 10 {} | 10 {3} | 5 {3,3} | yo'q | Haqiqiy 5 xujayrali (oddiy) | |
| G28 2[3]2[4]2[3]2 = [3,4,3] | 1152 | 12 | 2{3}2{4}2{3}2 = {3,4,3} | 24 | 96 {} | 96 {3} | 24 {3,4} | {6} | Haqiqiy 24-hujayra | |
| G30 2[3]2[3]2[5]2 = [3,3,5] | 14400 | 30 | 2{3}2{3}2{5}2 = {3,3,5} | 120 | 720 {} | 1200 {3} | 600 {3,3} | {10} | Haqiqiy 600 hujayra | |
| 2{5}2{3}2{3}2 = {5,3,3} | 600 | 1200 {} | 720 {5} | 120 {5,3} | Haqiqiy 120 hujayradan iborat | |||||
| G (2,1,4) 2[3]2[3]2[4]p =[3,3,4] | 384 | 8 | β2 4 = β4 = {3,3,4} | 8 | 24 {} | 32 {3} | 16 {3,3} | {4} | Haqiqiy 16 hujayradan iborat Xuddi shunday | |
| γ2 4 = γ4 = {4,3,3} | 16 | 32 {} | 24 {4} | 8 {4,3} | yo'q | Haqiqiy tesserakt {} Bilan bir xil4 yoki | ||||
| G (p, 1,4) 2[3]2[3]2[4]p p = 2,3,4, ... | 24p4 | 4p | βp 4 = 2{3}2{3}2{4}p | 4p | 6p2 {} | 4p3 {3} | p4 {3,3} | 2{4}p | Umumlashtirilgan 4-ortoppleks Xuddi shunday | |
| γp 4 = p{4}2{3}2{3}2 | p4 | 4p3 p{} | 6p2 p{4}2 | 4p p{4}2{3}2 | yo'q | Umumiy tesserakt Xuddi shunday p{}4 yoki | ||||
| G (3,1,4) 2[3]2[3]2[4]3 | 1944 | 12 | β3 4 = 2{3}2{3}2{4}3 | 12 | 54 {} | 108 {3} | 81 {3,3} | 2{4}3 | Umumlashtirilgan 4-ortoppleks Xuddi shunday | |
| γ3 4 = 3{4}2{3}2{3}2 | 81 | 108 3{} | 54 3{4}2 | 12 3{4}2{3}2 | yo'q | Xuddi shunday 3{}4 yoki | ||||
| G (4,1,4) 2[3]2[3]2[4]4 | 6144 | 16 | β4 4 = 2{3}2{3}2{4}4 | 16 | 96 {} | 256 {3} | 64 {3,3} | 2{4}4 | Xuddi shunday | |
| γ4 4 = 4{4}2{3}2{3}2 | 256 | 256 4{} | 96 4{4}2 | 16 4{4}2{3}2 | yo'q | Xuddi shunday 4{}4 yoki | ||||
| G (5,1,4) 2[3]2[3]2[4]5 | 15000 | 20 | β5 4 = 2{3}2{3}2{4}5 | 20 | 150 {} | 500 {3} | 625 {3,3} | 2{4}5 | Xuddi shunday | |
| γ5 4 = 5{4}2{3}2{3}2 | 625 | 500 5{} | 150 5{4}2 | 20 5{4}2{3}2 | yo'q | Xuddi shunday 5{}4 yoki | ||||
| G (6,1,4) 2[3]2[3]2[4]6 | 31104 | 24 | β6 4 = 2{3}2{3}2{4}6 | 24 | 216 {} | 864 {3} | 1296 {3,3} | 2{4}6 | Xuddi shunday | |
| γ6 4 = 6{4}2{3}2{3}2 | 1296 | 864 6{} | 216 6{4}2 | 24 6{4}2{3}2 | yo'q | Xuddi shunday 6{}4 yoki | ||||
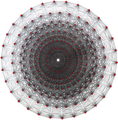
| G32 3[3]3[3]3[3]3 | 155520 | 30 | 3{3}3{3}3{3}3 | 240 | 2160 3{} | 2160 3{3}3 | 240 3{3}3{3}3 | 3{4}3 | Politop sifatida namoyish etish 421 |
Muntazam kompleks 4-politoplarning vizualizatsiyalari
Haqiqiy {3,3,3},






 , 5 ta tepalik, 10 ta qirradan, 10 {3} yuzdan va 5 ta {3,3} katakdan iborat edi
, 5 ta tepalik, 10 ta qirradan, 10 {3} yuzdan va 5 ta {3,3} katakdan iborat ediHaqiqiy {3,4,3},






 , 24 ta tepalik, 96 ta qirralar, 96 {3} yuzlar va 24 {3,4} hujayradan iborat edi
, 24 ta tepalik, 96 ta qirralar, 96 {3} yuzlar va 24 {3,4} hujayradan iborat ediHaqiqiy {5,3,3},






 , 600 tepalik, 1200 qirralar, 720 {5} yuzlar va 120 {5,3} hujayradan iborat edi
, 600 tepalik, 1200 qirralar, 720 {5} yuzlar va 120 {5,3} hujayradan iborat ediHaqiqiy {3,3,5},






 , 120 ta tepalik, 720 qirralar, 1200 {3} yuzlar va 600 {3,3} hujayradan iborat edi
, 120 ta tepalik, 720 qirralar, 1200 {3} yuzlar va 600 {3,3} hujayradan iborat ediPolitop,






 , 240 tepalik, 2160 3 qirrali, 2160 3 {3} 3 yuz va 240 3 {3} 3 {3} 3 katakka ega
, 240 tepalik, 2160 3 qirrali, 2160 3 {3} 3 yuz va 240 3 {3} 3 {3} 3 katakka ega
- Umumlashtirilgan 4-ortoplekslar
Umumlashtirilgan 4-ortoplekslar muntazam ravishda tuzilishga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]() va quasiregular shakli kabi
va quasiregular shakli kabi ![]()
![]()
![]()
![]()
![]()
![]() . Barcha elementlar simplekslar.
. Barcha elementlar simplekslar.
Haqiqiy {3,3,4},






 yoki
yoki 



 , 8 ta tepalik, 24 ta qirradan, 32 ta yuzdan va 16 ta katakdan iborat
, 8 ta tepalik, 24 ta qirradan, 32 ta yuzdan va 16 ta katakdan iborat
- Umumlashtirilgan 4 kubik
Umumiy tesseraktlar muntazam ravishda tuzilishga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]() va prizmatik qurilish kabi
va prizmatik qurilish kabi ![]()
![]()
![]()
![]()
![]()
![]()
![]() , to'rt kishilik mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
, to'rt kishilik mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
Haqiqiy {4,3,3},






 yoki
yoki 





 , 16 ta tepalik, 32 ta chekka, 24 ta yuz va 8 ta katakchadan iborat
, 16 ta tepalik, 32 ta chekka, 24 ta yuz va 8 ta katakchadan iborat
Muntazam kompleks 5-politoplarni sanash
Doimiy kompleks 5-politoplar yoki undan yuqori uch oilada mavjud, haqiqiy simplekslar va umumlashtirilgan giperkubva ortoppleks.
| Bo'shliq | Guruh | Buyurtma | Polytope | Vertices | Qirralar | Yuzlar | Hujayralar | 4 yuzlar | Van Oss ko'pburchak | Izohlar |
|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,5) = [3,3,3,3] | 720 | a5 = {3,3,3,3} | 6 | 15 {} | 20 {3} | 15 {3,3} | 6 {3,3,3} | yo'q | Haqiqiy 5-oddiy | |
| G (2,1,5) =[3,3,3,4] | 3840 | β2 5 = β5 = {3,3,3,4} | 10 | 40 {} | 80 {3} | 80 {3,3} | 32 {3,3,3} | {4} | Haqiqiy 5-ortoppleks Xuddi shunday | |
| γ2 5 = γ5 = {4,3,3,3} | 32 | 80 {} | 80 {4} | 40 {4,3} | 10 {4,3,3} | yo'q | Haqiqiy 5-kub {} Bilan bir xil5 yoki | |||
| G (p, 1,5) 2[3]2[3]2[3]2[4]p | 120p5 | βp 5 = 2{3}2{3}2{3}2{4}p | 5p | 10p2 {} | 10p3 {3} | 5p4 {3,3} | p5 {3,3,3} | 2{4}p | Umumlashtirildi 5-ortoppleks Xuddi shunday | |
| γp 5 = p{4}2{3}2{3}2{3}2 | p5 | 5p4 p{} | 10p3 p{4}2 | 10p2 p{4}2{3}2 | 5p p{4}2{3}2{3}2 | yo'q | Umumlashtirildi 5-kub Xuddi shunday p{}5 yoki | |||
| G (3,1,5) 2[3]2[3]2[3]2[4]3 | 29160 | β3 5 = 2{3}2{3}2{3}2{4}3 | 15 | 90 {} | 270 {3} | 405 {3,3} | 243 {3,3,3} | 2{4}3 | Xuddi shunday | |
| γ3 5 = 3{4}2{3}2{3}2{3}2 | 243 | 405 3{} | 270 3{4}2 | 90 3{4}2{3}2 | 15 3{4}2{3}2{3}2 | yo'q | Xuddi shunday 3{}5 yoki | |||
| G (4,1,5) 2[3]2[3]2[3]2[4]4 | 122880 | β4 5 = 2{3}2{3}2{3}2{4}4 | 20 | 160 {} | 640 {3} | 1280 {3,3} | 1024 {3,3,3} | 2{4}4 | Xuddi shunday | |
| γ4 5 = 4{4}2{3}2{3}2{3}2 | 1024 | 1280 4{} | 640 4{4}2 | 160 4{4}2{3}2 | 20 4{4}2{3}2{3}2 | yo'q | Xuddi shunday 4{}5 yoki | |||
| G (5,1,5) 2[3]2[3]2[3]2[4]5 | 375000 | β5 5 = 2{3}2{3}2{3}2{5}5 | 25 | 250 {} | 1250 {3} | 3125 {3,3} | 3125 {3,3,3} | 2{5}5 | Xuddi shunday | |
| γ5 5 = 5{4}2{3}2{3}2{3}2 | 3125 | 3125 5{} | 1250 5{5}2 | 250 5{5}2{3}2 | 25 5{4}2{3}2{3}2 | yo'q | Xuddi shunday 5{}5 yoki | |||
| G (6,1,5) 2[3]2[3]2[3]2[4]6 | 933210 | β6 5 = 2{3}2{3}2{3}2{4}6 | 30 | 360 {} | 2160 {3} | 6480 {3,3} | 7776 {3,3,3} | 2{4}6 | Xuddi shunday | |
| γ6 5 = 6{4}2{3}2{3}2{3}2 | 7776 | 6480 6{} | 2160 6{4}2 | 360 6{4}2{3}2 | 30 6{4}2{3}2{3}2 | yo'q | Xuddi shunday 6{}5 yoki |
Muntazam kompleks 5-politoplarning ingl
- Umumlashtirilgan 5-ortoplekslar
Umumlashtirilgan 5-ortoplekslar muntazam ravishda tuzilishga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() va quasiregular shakli kabi
va quasiregular shakli kabi ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Barcha elementlar simplekslar.
. Barcha elementlar simplekslar.
Haqiqiy {3,3,3,4},








 , 10 ta tepalik, 40 qirrali, 80 ta yuzli, 80 ta katakchali va 32 ta 4 yuzli
, 10 ta tepalik, 40 qirrali, 80 ta yuzli, 80 ta katakchali va 32 ta 4 yuzli
- Umumiy 5 kubik
Umumiylashtirilgan 5-kubiklar odatdagi konstruktsiyaga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() va kabi prizmatik qurilish
va kabi prizmatik qurilish ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , beshlik mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
, beshlik mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
Haqiqiy {4,3,3,3},








 , 32 tepalik, 80 chekka, 80 yuz, 40 katak va 10 4 yuzli
, 32 tepalik, 80 chekka, 80 yuz, 40 katak va 10 4 yuzli
Muntazam kompleks 6-politoplarni sanash
| Bo'shliq | Guruh | Buyurtma | Polytope | Vertices | Qirralar | Yuzlar | Hujayralar | 4 yuzlar | 5 yuzlar | Van Oss ko'pburchak | Izohlar |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,6) = [3,3,3,3,3] | 720 | a6 = {3,3,3,3,3} | 7 | 21 {} | 35 {3} | 35 {3,3} | 21 {3,3,3} | 7 {3,3,3,3} | yo'q | Haqiqiy 6-oddiy | |
| G (2,1,6) [3,3,3,4] | 46080 | β2 6 = β6 = {3,3,3,4} | 12 | 60 {} | 160 {3} | 240 {3,3} | 192 {3,3,3} | 64 {3,3,3,3} | {4} | Haqiqiy 6-ortoppleks Xuddi shunday | |
| γ2 6 = γ6 = {4,3,3,3} | 64 | 192 {} | 240 {4} | 160 {4,3} | 60 {4,3,3} | 12 {4,3,3,3} | yo'q | Haqiqiy 6-kub {} Bilan bir xil6 yoki | |||
| G (p, 1,6) 2[3]2[3]2[3]2[4]p | 720p6 | βp 6 = 2{3}2{3}2{3}2{4}p | 6p | 15p2 {} | 20p3 {3} | 15p4 {3,3} | 6p5 {3,3,3} | p6 {3,3,3,3} | 2{4}p | Umumlashtirildi 6-ortoppleks Xuddi shunday | |
| γp 6 = p{4}2{3}2{3}2{3}2 | p6 | 6p5 p{} | 15p4 p{4}2 | 20p3 p{4}2{3}2 | 15p2 p{4}2{3}2{3}2 | 6p p{4}2{3}2{3}2{3}2 | yo'q | Umumlashtirildi 6-kub Xuddi shunday p{}6 yoki |
Muntazam kompleks 6-politoplarning ingl
- Umumlashtirilgan 6-ortoplekslar
Umumlashtirilgan 6-ortopplekslar muntazam ravishda tuzilishga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() va quasiregular shakli kabi
va quasiregular shakli kabi ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Barcha elementlar simplekslar.
. Barcha elementlar simplekslar.
Haqiqiy {3,3,3,3,4},










 , 12 tepalik, 60 qirrali, 160 yuzli, 240 katakli, 192 4 yuzli va 64 5 yuzli
, 12 tepalik, 60 qirrali, 160 yuzli, 240 katakli, 192 4 yuzli va 64 5 yuzli
- Umumiy 6 kubik
Umumiylashtirilgan 6-kubiklar muntazam ravishda tuzilishga ega ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() va prizmatik qurilish kabi
va prizmatik qurilish kabi ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , oltidan iborat mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
, oltidan iborat mahsulot p-gonalli 1-politoplar. Elementlar pastki o'lchovli umumlashtirilgan kublardir.
Haqiqiy {3,3,3,3,3,4},










 , 64 tepalik, 192 chekka, 240 yuz, 160 hujayra, 60 4 yuzli va 12 5 yuzli
, 64 tepalik, 192 chekka, 240 yuz, 160 hujayra, 60 4 yuzli va 12 5 yuzli
Muntazam kompleks apeirotoplarni ro'yxatga olish
Kokseter bu yulduzsiz oddiy kompleks apeirotoplar yoki ko'plab chuqurchalar ro'yxatini sanab o'tdi.[33]
Har bir o'lchov uchun $ mathbb {g} $ belgisi bilan 12 ta apeyrotop mavjudp,r
n + 1 har qanday o'lchamlarda mavjud , yoki agar p=q= 2. Kokseter bu umumlashtirilgan kubik chuqurchalarini chaqiradi n>2.[34]
Ularning har birida mutanosib elementlar soni berilgan:
- k-yuzlari = , qayerda va n! belgisini bildiradi faktorial ning n.
Muntazam kompleks 1-politoplar
Yagona muntazam kompleks 1-politop ∞{} yoki ![]() . Uning haqiqiy vakili apeirogon, {∞} yoki
. Uning haqiqiy vakili apeirogon, {∞} yoki ![]()
![]()
![]() .
.
Muntazam kompleks apeyronlar
2-darajali murakkab apeyronlar simmetriyaga ega p[q]rqaerda 1 /p + 2/q + 1/r = 1. Kokseter ularni δ shaklida ifodalaydip,r
2 qayerda q qondirish uchun cheklangan q = 2/(1 – (p + r)/pr).[35]
8 ta echim mavjud:
| 2[∞]2 | 3[12]2 | 4[8]2 | 6[6]2 | 3[6]3 | 6[4]3 | 4[4]4 | 6[3]6 |
Ikkita g'alati echimlar mavjud q va tengsiz p va r: 10[5]2 va 12[3]4, yoki ![]()
![]()
![]() va
va ![]()
![]()
![]() .
.
Muntazam kompleks apeirogon p{q}r bor p- qirralarning va r- vertikal raqamlar. Ikkala apeirogon p{q}r bu r{q}p. Shaklning apeirogoni p{q}p o'z-o'zini dual. Shakl guruhlari p[2q]2 yarim simmetriyaga ega p[q]p, shuning uchun oddiy apeirogon ![]()
![]()
![]()
![]() quasiregular bilan bir xil
quasiregular bilan bir xil ![]()
![]()
![]() .[36]
.[36]
Apeirogonlarni Argand samolyoti to'rt xil vertex tartibini baham ko'ring. Shaklning apeyronlari 2{q}r {kabi vertikal tartibga ega bo'lingq/2,p}. Shakl p{q}2 r {sifatida vertikal tartibga egap,q/ 2}. Shaklning apeyronlari p{4}r vertikal kelishuvlarga ega {p,r}.
Afinaviy tugunlarni va shu jumladan , yana uchta cheksiz echim mavjud: ∞[2]∞, ∞[4]2, ∞[3]3va ![]()
![]()
![]() ,
, ![]()
![]()
![]() va
va ![]()
![]()
![]() . Birinchisi, ikkinchisining indeks 2 kichik guruhi. Ushbu apeyronlarning tepalari mavjud .
. Birinchisi, ikkinchisining indeks 2 kichik guruhi. Ushbu apeyronlarning tepalari mavjud .
| Bo'shliq | Guruh | Apeirogon | Yon | vakili.[37] | Rasm | Izohlar | |
|---|---|---|---|---|---|---|---|
| 2[∞]2 = [∞] | δ2,2 2 = {∞} | | {} | Haqiqiy apeirogon Xuddi shunday | |||
| / | ∞[4]2 | ∞{4}2 | ∞{} | {4,4} |  | Xuddi shunday  | |
| ∞[3]3 | ∞{3}3 | ∞{} | {3,6} | Xuddi shunday | |||
| p[q]r | δp, r 2 = p{q}r | p{} | |||||
| 3[12]2 | δ3,2 2 = 3{12}2 | 3{} | r {3,6} |  | Xuddi shunday  | ||
| δ2,3 2 = 2{12}3 | {} | {6,3} |  | ||||
| 3[6]3 | δ3,3 2 = 3{6}3 | 3{} | {3,6} | Xuddi shunday | |||
| 4[8]2 | δ4,2 2 = 4{8}2 | 4{} | {4,4} |  | Xuddi shunday  | ||
| δ2,4 2 = 2{8}4 | {} | {4,4} |  | ||||
| 4[4]4 | δ4,4 2 = 4{4}4 | 4{} | {4,4} |  | Xuddi shunday | ||
| 6[6]2 | δ6,2 2 = 6{6}2 | 6{} | r {3,6} | Xuddi shunday | |||
| δ2,6 2 = 2{6}6 | {} | {3,6} | |||||
| 6[4]3 | δ6,3 2 = 6{4}3 | 6{} | {6,3} |  | |||
| δ3,6 2 = 3{4}6 | 3{} | {3,6} | |||||
| 6[3]6 | δ6,6 2 = 6{3}6 | 6{} | {3,6} |  | Xuddi shunday | ||
Muntazam ravishda apeirohedra kompleksi
Formadagi 22 ta muntazam kompleks apeirohedra mavjud p{a}q{b}r. 8 - o'z-o'zini dual (p=r va a=b), ikkinchisi esa politop juftligi sifatida mavjud. Uchtasi butunlay haqiqiy (p=q=r=2).
Kokseter ularning 12 tasini δ shaklida anglatadip,r
3 yoki p{4}2{4}r apeirotop mahsulotining muntazam shakli hisoblanadip,r
2 × δp,r
2 yoki p{q}r × p{q}r, qayerda q dan aniqlanadi p va r.
![]()
![]()
![]()
![]()
![]() bilan bir xil
bilan bir xil ![]()
![]()
![]()
![]() , shu qatorda; shu bilan birga
, shu qatorda; shu bilan birga ![]()
![]()
![]()
![]()
![]()
![]()
![]() , uchun p,r= 2,3,4,6. Shuningdek
, uchun p,r= 2,3,4,6. Shuningdek ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() .[38]
.[38]
| Bo'shliq | Guruh | Apeyrohedr | Tepalik | Yon | Yuz | van Oss apeirogon | Izohlar | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2[3]2[4]∞ | ∞{4}2{3}2 | ∞{} | ∞{4}2 | Xuddi shunday ∞{}×∞{}×∞{} yoki Haqiqiy vakillik {4,3,4} | ||||||
| p[4]2[4]r | p{4}2{4}r | | p2 | 2pq | p{} | r2 | p{4}2 | 2{q}r | Xuddi shunday | |
| [4,4] | δ2,2 3 = {4,4} | 4 | 8 | {} | 4 | {4} | {∞} | Haqiqiy kvadrat plitka Xuddi shunday | ||
| 3[4]2[4]2 3[4]2[4]3 4[4]2[4]2 4[4]2[4]4 6[4]2[4]2 6[4]2[4]3 6[4]2[4]6 | 3{4}2{4}2 2{4}2{4}3 3{4}2{4}3 4{4}2{4}2 2{4}2{4}4 4{4}2{4}4 6{4}2{4}2 2{4}2{4}6 6{4}2{4}3 3{4}2{4}6 6{4}2{4}6 | 9 4 9 16 4 16 36 4 36 9 36 | 12 12 18 16 16 32 24 24 36 36 72 | 3{} {} 3{} 4{} {} 4{} 6{} {} 6{} 3{} 6{} | 4 9 9 4 16 16 4 36 9 36 36 | 3{4}2 {4} 3{4}2 4{4}2 {4} 4{4}2 6{4}2 {4} 6{4}2 3{4}2 6{4}2 | p{q}r | Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday Xuddi shunday | ||
| Bo'shliq | Guruh | Apeyrohedr | Tepalik | Yon | Yuz | van Oss apeirogon | Izohlar | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2[4]r[4]2 | 2{4}r{4}2 | | 2 | {} | 2 | p{4}2' | 2{4}r | Xuddi shunday | ||
| [4,4] | {4,4} | 2 | 4 | {} | 2 | {4} | {∞} | Xuddi shunday | ||
| 2[4]3[4]2 2[4]4[4]2 2[4]6[4]2 | 2{4}3{4}2 2{4}4{4}2 2{4}6{4}2 | 2 | 9 16 36 | {} | 2 | 2{4}3 2{4}4 2{4}6 | 2{q}r | Xuddi shunday Xuddi shunday Xuddi shunday | ||
| Bo'shliq | Guruh | Apeyrohedr | Tepalik | Yon | Yuz | van Oss apeirogon | Izohlar | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2[6]2[3]2 = [6,3] | {3,6} | | 1 | 3 | {} | 2 | {3} | {∞} | Haqiqiy uchburchak plitka | |
| {6,3} | 2 | 3 | {} | 1 | {6} | yo'q | Haqiqiy olti burchakli plitka | |||
| 3[4]3[3]3 | 3{3}3{4}3 | 1 | 8 | 3{} | 3 | 3{3}3 | 3{4}6 | Xuddi shunday | ||
| 3{4}3{3}3 | 3 | 8 | 3{} | 2 | 3{4}3 | 3{12}2 | ||||
| 4[3]4[3]4 | 4{3}4{3}4 | 1 | 6 | 4{} | 1 | 4{3}4 | 4{4}4 | Self-dual, xuddi shunday | ||
| 4[3]4[4]2 | 4{3}4{4}2 | 1 | 12 | 4{} | 3 | 4{3}4 | 2{8}4 | Xuddi shunday | ||
| 2{4}4{3}4 | 3 | 12 | {} | 1 | 2{4}4 | 4{4}4 | ||||
Muntazam kompleks 3-apeyrotoplar
16 muntazam apeyrotop mavjud . Kokseter ulardan 12 tasini δ bilan ifodalaydip,r
3 qayerda q qondirish uchun cheklangan q = 2/(1 – (p + r)/pr). Ular shuningdek mahsulot apeyrotoplari sifatida ajralib chiqishi mumkin: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Birinchi holat kubik chuqurchasi.
. Birinchi holat kubik chuqurchasi.
| Bo'shliq | Guruh | 3-apeyrotop | Tepalik | Yon | Yuz | Hujayra | van Oss apeirogon | Izohlar |
|---|---|---|---|---|---|---|---|---|
| p[4]2[3]2[4]r | δp,r 3 = p{4}2{3}2{4}r | p{} | p{4}2 | p{4}2{3}2 | p{q}r | Xuddi shunday | ||
| 2[4]2[3]2[4]2 =[4,3,4] | δ2,2 3 = 2{4}2{3}2{4}2 | {} | {4} | {4,3} | Kubik chuqurchalar Xuddi shunday | |||
| 3[4]2[3]2[4]2 | δ3,2 3 = 3{4}2{3}2{4}2 | 3{} | 3{4}2 | 3{4}2{3}2 | Xuddi shunday | |||
| δ2,3 3 = 2{4}2{3}2{4}3 | {} | {4} | {4,3} | Xuddi shunday | ||||
| 3[4]2[3]2[4]3 | δ3,3 3 = 3{4}2{3}2{4}3 | 3{} | 3{4}2 | 3{4}2{3}2 | Xuddi shunday | |||
| 4[4]2[3]2[4]2 | δ4,2 3 = 4{4}2{3}2{4}2 | 4{} | 4{4}2 | 4{4}2{3}2 | Xuddi shunday | |||
| δ2,4 3 = 2{4}2{3}2{4}4 | {} | {4} | {4,3} | Xuddi shunday | ||||
| 4[4]2[3]2[4]4 | δ4,4 3 = 4{4}2{3}2{4}4 | 4{} | 4{4}2 | 4{4}2{3}2 | Xuddi shunday | |||
| 6[4]2[3]2[4]2 | δ6,2 3 = 6{4}2{3}2{4}2 | 6{} | 6{4}2 | 6{4}2{3}2 | Xuddi shunday | |||
| δ2,6 3 = 2{4}2{3}2{4}6 | {} | {4} | {4,3} | Xuddi shunday | ||||
| 6[4]2[3]2[4]3 | δ6,3 3 = 6{4}2{3}2{4}3 | 6{} | 6{4}2 | 6{4}2{3}2 | Xuddi shunday | |||
| δ3,6 3 = 3{4}2{3}2{4}6 | 3{} | 3{4}2 | 3{4}2{3}2 | Xuddi shunday | ||||
| 6[4]2[3]2[4]6 | δ6,6 3 = 6{4}2{3}2{4}6 | 6{} | 6{4}2 | 6{4}2{3}2 | Xuddi shunday |
| Bo'shliq | Guruh | 3-apeyrotop | Tepalik | Yon | Yuz | Hujayra | van Oss apeirogon | Izohlar |
|---|---|---|---|---|---|---|---|---|
| 2[4]3[3]3[3]3 | 3{3}3{3}3{4}2 | 1 | 24 3{} | 27 3{3}3 | 2 3{3}3{3}3 | 3{4}6 | Xuddi shunday | |
| 2{4}3{3}3{3}3 | 2 | 27 {} | 24 2{4}3 | 1 2{4}3{3}3 | 2{12}3 | |||
| 2[3]2[4]3[3]3 | 2{3}2{4}3{3}3 | 1 | 27 {} | 72 2{3}2 | 8 2{3}2{4}3 | 2{6}6 | ||
| 3{3}3{4}2{3}2 | 8 | 72 3{} | 27 3{3}3 | 1 3{3}3{4}2 | 3{6}3 | Xuddi shunday |
Muntazam kompleksli 4-apeyrotoplar
Ichida 15 ta muntazam kompleks apeyrotop mavjud . Kokseter ulardan 12 tasini δ bilan ifodalaydip,r
4 qayerda q qondirish uchun cheklangan q = 2/(1 – (p + r)/pr). Ular shuningdek mahsulot apeyrotoplari sifatida ajralib chiqishi mumkin: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Birinchi holat tesseraktik asal. The 16 hujayrali chuqurchalar va 24 hujayrali chuqurchalar haqiqiy echimlar. Oxirgi echim ishlab chiqarilgan Politop elementlar.
. Birinchi holat tesseraktik asal. The 16 hujayrali chuqurchalar va 24 hujayrali chuqurchalar haqiqiy echimlar. Oxirgi echim ishlab chiqarilgan Politop elementlar.
| Bo'shliq | Guruh | 4-apeyrotop | Tepalik | Yon | Yuz | Hujayra | 4 yuz | van Oss apeirogon | Izohlar |
|---|---|---|---|---|---|---|---|---|---|
| p[4]2[3]2[3]2[4]r | δp,r 4 = p{4}2{3}2{3}2{4}r | p{} | p{4}2 | p{4}2{3}2 | p{4}2{3}2{3}2 | p{q}r | Xuddi shunday | ||
| 2[4]2[3]2[3]2[4]2 | δ2,2 4 = {4,3,3,3} | {} | {4} | {4,3} | {4,3,3} | {∞} | Tesseraktik asal Xuddi shunday | ||
| 2[3]2[4]2[3]2[3]2 =[3,4,3,3] | {3,3,4,3} | 1 | 12 {} | 32 {3} | 24 {3,3} | 3 {3,3,4} | Haqiqiy 16 hujayrali chuqurchalar Xuddi shunday | ||
| {3,4,3,3} | 3 | 24 {} | 32 {3} | 12 {3,4} | 1 {3,4,3} | Haqiqiy 24 hujayrali chuqurchalar Xuddi shunday | |||
| 3[3]3[3]3[3]3[3]3 | 3{3}3{3}3{3}3{3}3 | 1 | 80 3{} | 270 3{3}3 | 80 3{3}3{3}3 | 1 3{3}3{3}3{3}3 | 3{4}6 | vakillik 521 |
Muntazam kompleks 5-apeyrotoplar va undan yuqori
Faqat 12 ta muntazam kompleks apeyrotop mavjud yoki undan yuqori,[40] ifodalangan δp,r
n qayerda q qondirish uchun cheklangan q = 2/(1 – (p + r)/pr). Bular, shuningdek, mahsuloti parchalanishi mumkin n apeyronlar: ![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Birinchi holat haqiqiydir giperkubik chuqurchasi.
. Birinchi holat haqiqiydir giperkubik chuqurchasi.
| Bo'shliq | Guruh | 5-apeyrotoplar | Vertices | Yon | Yuz | Hujayra | 4 yuz | 5 yuz | van Oss apeirogon | Izohlar |
|---|---|---|---|---|---|---|---|---|---|---|
| p[4]2[3]2[3]2[3]2[4]r | δp,r 5 = p{4}2{3}2{3}2{3}2{4}r | p{} | p{4}2 | p{4}2{3}2 | p{4}2{3}2{3}2 | p{4}2{3}2{3}2{3}2 | p{q}r | Xuddi shunday | ||
| 2[4]2[3]2[3]2[3]2[4]2 =[4,3,3,3,4] | δ2,2 5 = {4,3,3,3,4} | {} | {4} | {4,3} | {4,3,3} | {4,3,3,3} | {∞} | 5 kubik chuqurchalar Xuddi shunday |
van Oss ko'pburchagi
A van Oss ko'pburchagi tekislikdagi muntazam ko'pburchakdir (haqiqiy tekislik) yoki unitar samolyot ) unda odatiy politopning qirrasi ham, tsentroidi ham yotadi va politop elementlaridan hosil bo'ladi. Hamma oddiy polipoplarda ham Van Oss ko'pburchaklari mavjud emas.
Masalan, van Oss ko'pburchagi oktaedr samolyotlari uning markazidan o'tadigan uchta kvadrat. Aksincha a kub van Oss ko'pburchagi yo'q, chunki qirradan markazga tekislik ikki kvadrat yuzni diagonal ravishda kesib o'tadi va kubning tekislikda joylashgan ikki qirrasi ko'pburchak hosil qilmaydi.
Cheksiz chuqurchalar ham bor van Oss apeyronlari. Masalan, haqiqiy kvadrat plitka va uchburchak plitka bor apeyronlar {∞} van Oss apeirogons.[41]
Agar u mavjud bo'lsa, van Oss ko'pburchagi shakldagi muntazam kompleks politop p{q}r{s}t... bor p- qirralar.
Muntazam bo'lmagan murakkab politoplar
Mahsulot kompleksi polipoplar
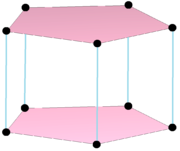 Murakkab mahsulot ko'pburchagi | 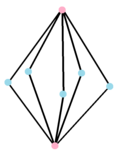 Ikki tomonlama ko'pburchak, {} +5{} has 7 vertices centered on the edges of the original, connected by 10 edges. Its real representation is a beshburchak bipiramida. |
Some complex polytopes can be represented as Kartezian mahsulotlari. These product polytopes are not strictly regular since they'll have more than one facet type, but some can represent lower symmetry of regular forms if all the orthogonal polytopes are identical. Masalan, mahsulot p{}×p{} or ![]()
![]()
![]() of two 1-dimensional polytopes is the same as the regular p{4}2 yoki
of two 1-dimensional polytopes is the same as the regular p{4}2 yoki ![]()
![]()
![]() . More general products, like p{}×q{} have real representations as the 4-dimensional p-q duoprizmalar. The dual of a product polytope can be written as a sum p{}+q{} and have real representations as the 4-dimensional p-q duopiramida. The p{}+p{} can have its symmetry doubled as a regular complex polytope 2{4}p yoki
. More general products, like p{}×q{} have real representations as the 4-dimensional p-q duoprizmalar. The dual of a product polytope can be written as a sum p{}+q{} and have real representations as the 4-dimensional p-q duopiramida. The p{}+p{} can have its symmetry doubled as a regular complex polytope 2{4}p yoki ![]()
![]()
![]() .
.
Xuddi shunday, a complex polyhedron can be constructed as a triple product: p{}×p{}×p{} or ![]()
![]()
![]()
![]()
![]() is the same as the regular generalized cube, p{4}2{3}2 yoki
is the same as the regular generalized cube, p{4}2{3}2 yoki ![]()
![]()
![]()
![]()
![]() , as well as product p{4}2×p{} or
, as well as product p{4}2×p{} or ![]()
![]()
![]()
![]()
![]() .[42]
.[42]
Quasiregular polygons
A quasiregular polygon is a qisqartirish of a regular polygon. A quasiregular polygon ![]()
![]()
![]() contains alternate edges of the regular polygons
contains alternate edges of the regular polygons ![]()
![]()
![]() va
va ![]()
![]()
![]() . The quasiregular polygon has p vertices on the p-edges of the regular form.
. The quasiregular polygon has p vertices on the p-edges of the regular form.
Quasiregular apeirogons
There are 7 quasiregular complex apeirogons which alternate edges of a regular apeirogon and its regular dual. The vertex arrangements of these apeirogon have real representations with the regular and uniform tilings of the Euclidean plane. The last column for the 6{3}6 apeirogon is not only self-dual, but the dual coincides with itself with overlapping hexagonal edges, thus their quasiregular form also has overlapping hexagonal edges, so it can't be drawn with two alternating colors like the others. The symmetry of the self-dual families can be doubled, so creating an identical geometry as the regular forms: ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
| p[q]r | 4[8]2 | 4[4]4 | 6[6]2 | 6[4]3 | 3[12]2 | 3[6]3 | 6[3]6 |
|---|---|---|---|---|---|---|---|
| Muntazam |  |  |  |  |  |  |  |
| Quasiregular |  |  |  |  |  |  |  |
| Regular dual |  |  |  |  |  |  |  |
Quasiregular polyhedra
Like real polytopes, a complex quasiregular polyhedron can be constructed as a tuzatish (a complete qisqartirish) of a regular polyhedron. Vertices are created mid-edge of the regular polyhedron and faces of the regular polyhedron and its dual are positioned alternating across common edges.
For example, a p-generalized cube, ![]()
![]()
![]()
![]()
![]() , bor p3 vertices, 3p2 edges, and 3p p-generalized square faces, while the p-generalized octahedron,
, bor p3 vertices, 3p2 edges, and 3p p-generalized square faces, while the p-generalized octahedron, ![]()
![]()
![]()
![]()
![]() , has 3p vertices, 3p2 qirralarning va p3 triangular faces. The middle quasiregular form p-generalized cuboctahedron,
, has 3p vertices, 3p2 qirralarning va p3 triangular faces. The middle quasiregular form p-generalized cuboctahedron, ![]()
![]()
![]()
![]()
![]() , has 3p2 vertices, 3p3 edges, and 3p+p3 yuzlar.
, has 3p2 vertices, 3p3 edges, and 3p+p3 yuzlar.
Also the tuzatish ning Hessian polyhedron ![]()
![]()
![]()
![]()
![]() , bo'ladi
, bo'ladi ![]()
![]()
![]()
![]()
![]() , a quasiregular form sharing the geometry of the regular complex polyhedron
, a quasiregular form sharing the geometry of the regular complex polyhedron ![]()
![]()
![]()
![]()
![]() .
.
| Generalized cube/octahedra | Hessian polyhedron | |||||
|---|---|---|---|---|---|---|
| p=2 (real) | p = 3 | p = 4 | p = 5 | p = 6 | ||
| Umumlashtirildi kublar (muntazam) |  Kub | 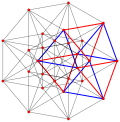 |  | 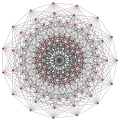 |  |  |
| Umumlashtirildi kuboktaedra (quasiregular) | 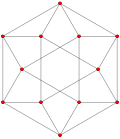 Kubokededr | 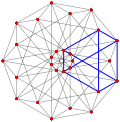 |  | 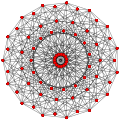 | 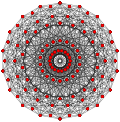 | 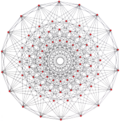 |
| Umumlashtirildi oktaedra (muntazam) |  Oktaedr | 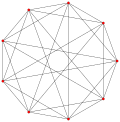 |  |  |  |  |
Other complex polytopes with unitary reflections of period two
Other nonregular complex polytopes can be constructed within unitary reflection groups that don't make linear Coxeter graphs. In Coxeter diagrams with loops Coxeter marks a special period interior, like ![]()
![]()
![]() or symbol (11 1 1)3, and group [1 1 1]3.[43][44] These complex polytopes have not been systematically explored beyond a few cases.
or symbol (11 1 1)3, and group [1 1 1]3.[43][44] These complex polytopes have not been systematically explored beyond a few cases.
Guruh ![]()
![]()
![]() is defined by 3 unitary reflections, R1, R2, R3, all order 2: R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R1)p = 1. The period p sifatida ko'rish mumkin ikki marta aylanish haqiqatda .
is defined by 3 unitary reflections, R1, R2, R3, all order 2: R12 = R12 = R32 = (R1R2)3 = (R2R3)3 = (R3R1)3 = (R1R2R3R1)p = 1. The period p sifatida ko'rish mumkin ikki marta aylanish haqiqatda .
Hammada bo'lgani kabi Wythoff konstruktsiyalari, polytopes generated by reflections, the number of vertices of a single-ringed Coxeter diagram polytope is equal to the order of the group divided by the order of the subgroup where the ringed node is removed. For example, a real kub has Coxeter diagram ![]()
![]()
![]()
![]()
![]() , bilan oktahedral simmetriya
, bilan oktahedral simmetriya ![]()
![]()
![]()
![]()
![]() order 48, and subgroup dihedral symmetry
order 48, and subgroup dihedral symmetry ![]()
![]()
![]() order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example
order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example ![]()
![]()
![]() for the cube. Vertex raqamlari are generated by removing a ringed node and ringing one or more connected nodes, and
for the cube. Vertex raqamlari are generated by removing a ringed node and ringing one or more connected nodes, and ![]()
![]()
![]() for the cube.
for the cube.
Coxeter represents these groups by the following symbols. Some groups have the same order, but a different structure, defining the same vertikal tartibga solish in complex polytopes, but different edges and higher elements, like ![]()
![]()
![]() va
va ![]()
![]()
![]()
![]() bilan p≠3.[45]
bilan p≠3.[45]
| Coxeter diagram | Buyurtma | Symbol or Position in Table VII of Shephard and Todd (1954) |
|---|---|---|
| pn − 1 n!, p ≥ 3 | G(p, p, n), [p], [1 1 1]p, [1 1 (n−2)p]3 | |
| 72·6!, 108·9! | Nos. 33, 34, [1 2 2]3, [1 2 3]3 | |
| 14·4!, 3·6!, 64·5! | Nos. 24, 27, 29 |
Coxeter calls some of these complex polyhedra almost regular because they have regular facets and vertex figures. The first is a lower symmetry form of the generalized cross-polytope in . The second is a fractional generalized cube, reducing p-edges into single vertices leaving ordinary 2-edges. Three of them are related to the finite regular skew polyhedron yilda .
| Bo'shliq | Guruh | Buyurtma | Kokseter belgilar | Vertices | Qirralar | Faces | Tepalik shakl | Izohlar |
|---|---|---|---|---|---|---|---|---|
| [1 1 1p]3 p=2,3,4... | 6p2 | (1 1 11p)3 | 3p | 3p2 | {3} | {2p} | Shephard symbol (1 1; 11)p same as βp 3 = | |
| (11 1 1p)3 | p2 | {3} | {6} | Shephard symbol (11 1; 1)p 1/p γp 3 | ||||
| [1 1 12]3 | 24 | (1 1 112)3 | 6 | 12 | 8 {3} | {4} | Same as β2 3 = | |
| (11 1 12)3 | 4 | 6 | 4 {3} | {3} | 1/2 γ2 3 = | |||
| [1 1 1]3 | 54 | (1 1 11)3 | 9 | 27 | {3} | {6} | Shephard symbol (1 1; 11)3 same as β3 3 = | |
| (11 1 1)3 | 9 | 27 | {3} | {6} | Shephard symbol (11 1; 1)3 1/3 γ3 3 = β3 3 | |||
| [1 1 14]3 | 96 | (1 1 114)3 | 12 | 48 | {3} | {8} | Shephard symbol (1 1; 11)4 same as β4 3 = | |
| (11 1 14)3 | 16 | {3} | {6} | Shephard symbol (11 1; 1)4 1/4 γ4 3 | ||||
| [1 1 15]3 | 150 | (1 1 115)3 | 15 | 75 | {3} | {10} | Shephard symbol (1 1; 11)5 same as β5 3 = | |
| (11 1 15)3 | 25 | {3} | {6} | Shephard symbol (11 1; 1)5 1/5 γ5 3 | ||||
| [1 1 16]3 | 216 | (1 1 116)3 | 18 | 216 | {3} | {12} | Shephard symbol (1 1; 11)6 same as β6 3 = | |
| (11 1 16)3 | 36 | {3} | {6} | Shephard symbol (11 1; 1)6 1/6 γ6 3 | ||||
| [1 1 14]4 | 336 | (1 1 114)4 | 42 | 168 | 112 {3} | {8} | representation {3,8|,4} = {3,8}8 | |
| (11 1 14)4 | 56 | {3} | {6} | |||||
| [1 1 15]4 | 2160 | (1 1 115)4 | 216 | 1080 | 720 {3} | {10} | representation {3,10|,4} = {3,10}8 | |
| (11 1 15)4 | 360 | {3} | {6} | |||||
| [1 1 14]5 | (1 1 114)5 | 270 | 1080 | 720 {3} | {8} | representation {3,8|,5} = {3,8}10 | ||
| (11 1 14)5 | 360 | {3} | {6} |
Coxeter defines other groups with anti-unitary constructions, for example these three. The first was discovered and drawn by Piter MakMullen 1966 yilda.[47]
| Bo'shliq | Guruh | Buyurtma | Kokseter belgilar | Vertices | Qirralar | Faces | Tepalik shakl | Izohlar |
|---|---|---|---|---|---|---|---|---|
| [1 14 14](3) | 336 | (11 14 14)(3) | 56 | 168 | 84 {4} | {6} | representation {4,6|,3} = {4,6}6 | |
| [15 14 14](3) | 2160 | (115 14 14)(3) | 216 | 1080 | 540 {4} | {10} | representation {4,10|,3} = {4,10}6 | |
| [14 15 15](3) | (114 15 15)(3) | 270 | 1080 | 432 {5} | {8} | representation {5,8|,3} = {5,8}6 |
| Bo'shliq | Guruh | Buyurtma | Kokseter belgilar | Vertices | Boshqalar elementlar | Hujayralar | Tepalik shakl | Izohlar |
|---|---|---|---|---|---|---|---|---|
| [1 1 2p]3 p=2,3,4... | 24p3 | (1 1 22p)3 | 4p | Shephard (22 1; 1)p same as βp 4 = | ||||
| (11 1 2p )3 | p3 | Shephard (2 1; 11)p 1/p γp 4 | ||||||
| [1 1 22]3 =[31,1,1] | 192 | (1 1 222)3 | 8 | 24 edges 32 faces | 16 | β2 4 = | ||
| (11 1 22 )3 | 1/2 γ2 4 = 4, haqiqiy 16 hujayradan iborat | |||||||
| [1 1 2]3 | 648 | (1 1 22)3 | 12 | Shephard (22 1; 1)3 same as β3 4 = | ||||
| (11 1 23)3 | 27 | Shephard (2 1; 11)3 1/3 γ3 4 | ||||||
| [1 1 24]3 | 1536 | (1 1 224)3 | 16 | Shephard (22 1; 1)4 same as β4 4 = | ||||
| (11 1 24 )3 | 64 | Shephard (2 1; 11)4 1/4 γ4 4 | ||||||
| [14 1 2]3 | 7680 | (22 14 1)3 | 80 | Shephard (22 1; 1)4 | ||||
| (114 1 2)3 | 160 | Shephard (2 1; 11)4 | ||||||
| (11 14 2)3 | 320 | Shephard (2 11; 1)4 | ||||||
| [1 1 2]4 | (1 1 22)4 | 80 | 640 edges 1280 triangles | 640 | ||||
| (11 1 2)4 | 320 |
| Bo'shliq | Guruh | Buyurtma | Kokseter belgilar | Vertices | Qirralar | Yuzlari | Tepalik shakl | Izohlar |
|---|---|---|---|---|---|---|---|---|
| [1 1 3p]3 p=2,3,4... | 120p4 | (1 1 33p)3 | 5p | Shephard (33 1; 1)p same as βp 5 = | ||||
| (11 1 3p)3 | p4 | Shephard (3 1; 11)p 1/p γp 5 | ||||||
| [2 2 1]3 | 51840 | (2 1 22)3 | 80 | Shephard (2 1; 22)3 | ||||
| (2 11 2)3 | 432 | Shephard (2 11; 2)3 |
| Bo'shliq | Guruh | Buyurtma | Kokseter belgilar | Vertices | Qirralar | Yuzlari | Tepalik shakl | Izohlar |
|---|---|---|---|---|---|---|---|---|
| [1 1 4p]3 p=2,3,4... | 720p5 | (1 1 44p)3 | 6p | Shephard (44 1; 1)p same as βp 6 = | ||||
| (11 1 4p)3 | p5 | Shephard (4 1; 11)p 1/p γp 6 | ||||||
| [1 2 3]3 | 39191040 | (2 1 33)3 | 756 | Shephard (2 1; 33)3 | ||||
| (22 1 3)3 | 4032 | Shephard (22 1; 3)3 | ||||||
| (2 11 3)3 | 54432 | Shephard (2 11; 3)3 |
Vizualizatsiya
(1 1 22)4,




 has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.[52]
has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.[52]
Shuningdek qarang
Izohlar
- ^ Peter Orlik, Viktor Reyner, Anne V. Shepler. Shephard guruhlari uchun belgi vakili. Matematik Annalen. 2002 yil mart, 322-jild, 3-son, 477–492-betlar. DOI: 10.1007 / s002080200001 [1]
- ^ Kokseter, muntazam kompleks politoplar, p. 115
- ^ Kokseter, Muntazam kompleks polipoplar, 11.3 Petrie Polygon, oddiy h-gon formed by the orbit of the flag (O0, O0O1) for the product of the two generating reflections of any nonstarry regular complex polygon, p1{q}p2.
- ^ Complex Regular Polytopes,11.1 Regular complex polygons 103-bet
- ^ Shephard, 1952; "It is from considerations such as these that we derive the notion of the interior of a polytope, and it will be seen that in unitary space where the numbers cannot be so ordered such a concept of interior is impossible. [Para break] Hence ... we have to consider unitary polytopes as configurations."
- ^ Coxeter, Regular Complex polytopes, p. 96
- ^ Kokseter, muntazam kompleks politoplar, p. xiv
- ^ Coxeter, Complex Regular Polytopes, p. 177, Table III
- ^ Lehrer & Taylor 2009, p.87
- ^ Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. 178–179 betlar
- ^ Complex Polytopes, 8.9 The Two-Dimensional Case, s.88
- ^ Regular Complex Polytopes, Coxeter, pp.177-179
- ^ Kokseter, muntazam kompleks politoplar, p. 108
- ^ Kokseter, muntazam kompleks politoplar, p. 108
- ^ Kokseter, muntazam kompleks politoplar, p. 109
- ^ Kokseter, muntazam kompleks politoplar, p. 111
- ^ Kokseter, muntazam kompleks politoplar, p. 30 diagram and p. 47 indices for 8 3-edges
- ^ Kokseter, muntazam kompleks politoplar, p. 110
- ^ Kokseter, muntazam kompleks politoplar, p. 110
- ^ Kokseter, muntazam kompleks politoplar, p. 48
- ^ Kokseter, muntazam kompleks politoplar, p. 49
- ^ Coxeter, Regular Complex Polytopes, pp. 116–140.
- ^ Coxeter, Regular Complex Polytopes, pp. 118–119.
- ^ Coxeter, Regular Complex Polytopes, pp. 118-119
- ^ Complex Regular Polytopes, p.29
- ^ Coxeter, Regular Complex Polytopes, Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.
- ^ Kokseter, Kaleidoscopes — Selected Writings of H.S.M. Kokseter, Paper 25 Surprising relationships among unitary reflection groups, p. 431.
- ^ Kokseter, muntazam kompleks politoplar, p. 131
- ^ Kokseter, muntazam kompleks politoplar, p. 126
- ^ Kokseter, muntazam kompleks politoplar, p. 125
- ^ Kokseter, muntazam kompleks politoplar, p. 131
- ^ Coxeter, Regular Complex Polytopes, Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.
- ^ Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 180.
- ^ Complex regular polytope, p.174
- ^ Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 111, 136.
- ^ Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. 178–179 betlar
- ^ Coxeter, Regular Complex Polytopes, 11.6 Apeirogons, pp. 111-112
- ^ Coxeter, Complex Regular Polytopes, p.140
- ^ Coxeter, Regular Complex Polytopes, pp. 139-140
- ^ Complex Regular Polytopes, p.146
- ^ Complex Regular Polytopes, p.141
- ^ Coxeter, Regular Complex Polytopes, pp. 118–119, 138.
- ^ Coxeter, Regular Complex Polytopes, Chapter 14, Almost regular polytopes, pp. 156–174.
- ^ Kokseter, Groups Generated by Unitary Reflections of Period Two, 1956
- ^ Kokseter, Unitar aks ettirish natijasida hosil bo'lgan cheklangan guruhlar, 1966, 4. Grafik yozuv, Table of n-dimensional groups generated by n Unitary Reflections. pp. 422-423
- ^ Coxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
- ^ Coxeter, Complex Regular Polytopes, (1991), 14.6 McMullen's two polyhedral with 84 square faces, pp.166-171
- ^ Coxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
- ^ Coxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
- ^ Coxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
- ^ Coxeter, Groups generated by Unitary Reflections of Period Two (1956), Table III: Some Complex Polytopes, p.413
- ^ Coxeter, Complex Regular Polytopes, pp.172-173
Adabiyotlar
- Kokseter, H. S. M. and Moser, W. O. J.; Diskret guruhlar uchun generatorlar va aloqalar (1965), esp pp 67–80.
- Kokseter, X.S.M. (1991), Muntazam kompleks polipoplar, Kembrij universiteti matbuoti, ISBN 0-521-39490-2
- Kokseter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244,
- Shephard, G.C.; Muntazam kompleks politoplar, Proc. London math. Soc. Series 3, Vol 2, (1952), pp 82–97.
- G. C. Shephard, J. A. Todd, Finite unitary reflection groups, Canadian Journal of Mathematics. 6(1954), 274-304 [2][doimiy o'lik havola]
- Gustav I. Lehrer and Donald E. Taylor, Unitary Reflection Groups, Kembrij universiteti matbuoti 2009 yil
Qo'shimcha o'qish
| Vikimedia Commons-ga tegishli ommaviy axborot vositalari mavjud Complex polytopes. |
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson and Asia Ivić Weiss, editors: Kaleidoscopes — Selected Writings of H.S.M. Coxeter., Paper 25, Finite groups generated by unitary reflections, p 415-425, John Wiley, 1995, ISBN 0-471-01003-0
- MakMullen, Piter; Shulte, Egon (2002 yil dekabr), Abstrakt muntazam polipoplar (1-nashr), Kembrij universiteti matbuoti, ISBN 0-521-81496-0 9-bob Unitary Groups and Hermitian Forms, pp. 289–298









![{ displaystyle left [{ begin {smallmatrix} e ^ {2 pi i / p} & 0 (e ^ {2 pi i / p} -1) k & 1 end {smallmatrix}} o'ng ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128407ddca614c4bed7308acba9bd274b704c5c)
![{ displaystyle left [{ begin {smallmatrix} 1 & (e ^ {2 pi i / r} -1) k 0 & e ^ {2 pi i / r} end {smallmatrix}} o'ng ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7bd24e7be60162da1fa1566fea5571820d3e82)

![{ displaystyle left [{ begin {smallmatrix} e ^ {2 pi i / p} & 0 0 & 1 end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922057855ba2380fdbf36b0e91f0afe08b867bcb)
![{ displaystyle left [{ begin {smallmatrix} 1 & 0 0 & e ^ {2 pi i / q} end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6991a4012a94e23b3475fd268007ca2aeba4bcbe)
![{ displaystyle left [{ begin {smallmatrix} 0 & 1 1 & 0 end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9694a3311550c844e792232f8c8742c6f3c9d32f)
![{ displaystyle left [{ begin {smallmatrix} { frac {-1 + { sqrt {3}} i} {2}} & 0 { frac {-3 + { sqrt {3}} i } {2}} va 1 end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef7975113174eb40a8488733bebb8fb4d1bd293)
![{ displaystyle left [{ begin {smallmatrix} 1 & { frac {-3 + { sqrt {3}} i} {2}} 0 & { frac {-1 + { sqrt {3}} i} {2}} end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081ee946ee626dd6ae6d776581d567006cd16fb)
![{ displaystyle left [{ begin {smallmatrix} i & 0 0 & 1 end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4087d1ec8773364a46947bc9f58bf721a413846c)
![{ displaystyle left [{ begin {smallmatrix} 1 & 0 0 & i end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3736413b59866ae2edd640f7bb77f7b8bdd6a9d)
![{ displaystyle left [{ begin {smallmatrix} 1 & -2 0 & -1 end {smallmatrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de49a4aea18b37177252a0f6c2a3707c14b9b910)