WikiDer > Konus (toifalar nazariyasi)
Yilda toifalar nazariyasi, filiali matematika, funktsional konus ni aniqlash uchun ishlatiladigan mavhum tushuncha chegara shundan funktsiya. Konuslar toifalar nazariyasida ham boshqa ko'rinishga ega.
Ta'rif
Ruxsat bering F : J → C bo'lishi a diagramma yilda C. Rasmiy ravishda diagramma a dan boshqa narsa emas funktsiya dan J ga C. Terminologiyaning o'zgarishi biz o'ylagan haqiqatni aks ettiradi F oilasini indeksatsiya qilish kabi ob'ektlar va morfizmlar yilda C. The toifasi J "indeks toifasi" deb o'ylashadi. Buni an tushunchasi bilan taqqoslash kerak indekslangan oila ob'ektlar to'plam nazariyasi. Asosiy farq shundaki, bu erda bizda ham morfizmlar mavjud. Shunday qilib, masalan, qachon J a diskret kategoriya, bu to'plam nazariyasida indekslangan oila g'oyasiga eng mos keladi. Yana bir keng tarqalgan va qiziqroq misol J bo'lish a oraliq. J shuningdek, eng oddiy konuslarga olib keladigan bo'sh toifaga aylanishi mumkin.
Ruxsat bering N ob'ekti bo'lish C. A konus dan N ga F morfizmlar turkumi
har bir ob'ekt uchun X ning J, har bir morfizm uchun shunday f : X → Y yilda J quyidagi diagramma qatnovlar:
Ushbu uchburchaklar (odatda cheksiz) to'plami a shaklida tasvirlangan (qisman) konus tepalik bilan N. Ba'zan konusga ega deyiladi tepalik N va tayanch F.
Shuningdek, ni belgilash mumkin ikkilamchi tushunchasi a konus dan F ga N (shuningdek, a konus) yuqoridagi barcha o'qlarni orqaga qaytarish orqali. Shubhasiz, dan ko-konus F ga N morfizmlar turkumi
har bir ob'ekt uchun X ning J, har bir morfizm uchun shunday f : X → Y yilda J quyidagi diagramma qatnovi:
Ekvivalent formulalar
Bir qarashda konuslar toifalar nazariyasida biroz g'ayritabiiy konstruktsiyalarga o'xshaydi. Ular an xaritalari ob'ekt a funktsiya (yoki aksincha). Kategoriyalar nazariyasi ruhiga muvofiq biz ularni morfizm yoki mos keladigan toifadagi ob'ektlar sifatida aniqlamoqchimiz. Aslida, biz ikkalasini ham qila olamiz.
Ruxsat bering J kichik toifaga bo'ling va ruxsat bering CJ bo'lishi diagrammalar toifasi turdagi J yilda C (bu a dan boshqa narsa emas funktsiya toifasi). Aniqlang diagonal funktsiya Δ: C → CJ quyidagicha: Δ (N) : J → C bo'ladi doimiy funktsiya ga N Barcha uchun N yilda C.
Agar F turi diagrammasi J yilda C, quyidagi bayonotlar tengdir:
- ψ - bu konus N ga F
- a a tabiiy o'zgarish Δ dan (N) ga F
- (N, ψ) - ob'ekt vergul toifasi (Δ ↓ F)
Ikkala bayonotlar ham teng:
- ψ - dan ko-konus F ga N
- a a tabiiy o'zgarish dan F Δ ga (N)
- (N, ψ) - ob'ekt vergul toifasi (F ↓ Δ)
Ushbu bayonotlarning barchasi ta'riflarni to'g'ridan-to'g'ri qo'llash orqali tasdiqlanishi mumkin. Konuslarni tabiiy o'zgarish deb o'ylab, ular shunchaki morfizm ekanliklarini ko'ramiz CJ manba (yoki maqsad) doimiy funktsiyali bilan.
Konusning toifasi
Yuqoridagilarga ko'ra biz konusning toifasi F vergul toifasi sifatida (Δ ↓ F). Konuslarning morfizmlari bu toifadagi morfizmlardir. Ushbu ekvivalentlik doimiy funktsiyalar orasidagi tabiiy xarita Δ (N), Δ (M) orasidagi morfizmga to'g'ri keladi N va M. Shu ma'noda, diagonali funktsiya o'qlarga ahamiyatsiz ta'sir qiladi. Xuddi shunday nuqtai nazardan, doimiy xaritadan tabiiy xaritaning ta'rifini yozish Δ (N) ga F yuqoridagi kabi diagrammani beradi. Kutilganidek, konusdan morfizm (N, ψ) konusga (L, φ) shunchaki morfizmdir N → L shunday qilib, barcha "aniq" diagrammalar qatnaydi (keyingi qismdagi birinchi diagramaga qarang).
Xuddi shunday, dan ko-konuslar toifasi F vergul toifasi (F ↓ Δ).
Umumjahon konuslar
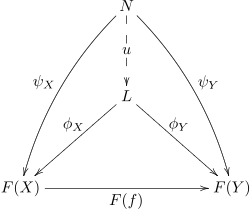
Cheklar va kolimitlar sifatida belgilanadi universal konuslar. Ya'ni, barcha boshqa konuslar omil qiladigan konuslar. Con dan konus L ga F con dan boshqa konus uchun universal konusdir N ga F ψ dan φgacha noyob morfizm mavjud.
Bunga teng ravishda, universal konus F a universal morfizm Δ dan to F (ob'ekt sifatida o'ylangan CJ), yoki a terminal ob'ekti ichida (Δ ↓)F).
Ikki marta, a dan konus F ga L con dan boshqa konus uchun universal konusdir F ga N φ dan ψgacha noyob morfizm mavjud.
Bunga teng ravishda, universal konus F dan boshlab universal morfizmdir F Δ ga yoki an ga boshlang'ich ob'ekt ichida (F ↓ Δ).
Chegarasi F uchun universal konus F, va kolimit - bu universal konus F. Barcha universal konstruktsiyalarda bo'lgani kabi, universal konuslarning ham barcha diagrammalar uchun mavjudligiga kafolat berilmaydi F, ammo agar ular mavjud bo'lsa, ular noyob izomorfizmgacha (vergul kategoriyasida (Δ ↓)F)).
Adabiyotlar
- Mac Leyn, Sonders (1998). Ishchi matematik uchun toifalar (2-nashr). Nyu-York: Springer. ISBN 0-387-98403-8.
- Borseux, Frensis (1994). "Cheklovlar". Kategorik algebra bo'yicha qo'llanma. Matematika entsiklopediyasi va uning qo'llanmalari 50-51, 53 [ya'ni. 52]. Jild 1. Kembrij universiteti matbuoti. ISBN 0-521-44178-1.