WikiDer > Masofa geometriyasi

Masofa geometriyasi bo'ladi tavsiflash va o'rganish to'plamlar asoslangan fikrlar faqat ning berilgan qiymatlari bo'yicha masofalar a'zo juftlari o'rtasida.^[1][2][3] Keyinchalik mavhumroq, bu o'rganishdir semimetrik bo'shliqlar va izometrik transformatsiyalar ular orasida. Shu nuqtai nazardan, uni sub'ekt sifatida ko'rib chiqish mumkin umumiy topologiya.^[4]

Tarixiy jihatdan masofa geometriyasidagi birinchi natija Heron formulasi milodiy 1-asrda. Zamonaviy nazariya 19-asrda asarlar bilan boshlandi Artur Keyli, undan keyin 20-asrda yanada kengroq o'zgarishlar yuz berdi Karl Menger va boshqalar.

Masofadagi geometriya muammolari nuqta konfiguratsiyasi shaklini chiqarish kerak bo'lganda paydo bo'ladi (nisbiy pozitsiyalar) orasidagi masofalardan, masalan biologiya,^[4] sensorlar tarmog'i,^[5] geodeziya, navigatsiya, kartografiyava fizika.

Kirish va ta'riflar

Masofa geometriyasi tushunchalari avval ikkita alohida masalani tavsiflash orqali tushuntiriladi.

Giperbolik navigatsiya masalasi

Birinchi muammo: giperbolik navigatsiya

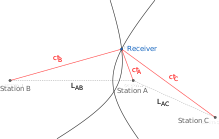
Joylari ma'lum bo'lgan uchta A, B, C yer usti radiostansiyalarini ko'rib chiqing. Radio qabul qilgich noma'lum joyda. Radio signalining stantsiyalardan qabul qiluvchiga o'tish vaqti, ${ displaystyle { displaystyle t_ {A}, t_ {B}, t_ {C}}}$, noma'lum, ammo vaqt farqlari, ${ displaystyle { displaystyle t_ {A} -t_ {B}}}$ va ${ displaystyle { displaystyle t_ {A} -t_ {C}}}$, ma'lum. Ulardan odam masofa farqlarini biladi ${ displaystyle c ({ displaystyle t_ {A} -t_ {B}})}$ va ${ displaystyle c ({ displaystyle t_ {A} -t_ {C}})}$, undan qabul qiluvchining pozitsiyasini topish mumkin.

Ikkinchi muammo: o'lchovni kamaytirish

Yilda ma'lumotlarni tahlil qilish, biriga ko'pincha vektor sifatida ko'rsatilgan ma'lumotlar ro'yxati beriladi ${ displaystyle mathbf {v} = (x_ {1}, cdots, x_ {n}) in mathbb {R} ^ {n}}$va ularning past o'lchovli affinali subspace ichida joylashganligini aniqlash kerak. Ma'lumotlarning past o'lchovli namoyishi juda ko'p afzalliklarga ega, masalan, saqlash joyini tejash, hisoblash vaqti va ma'lumotlar haqida yaxshiroq ma'lumot berish.

Ta'riflar

Endi biz o'z muammolarimizni ko'rib chiqishdan kelib chiqadigan ba'zi ta'riflarni rasmiylashtiramiz.

Semimetrik bo'shliq

Belgilangan fikrlar ro'yxati berilgan ${ displaystyle R = {P_ {0}, cdots, P_ {n} }}$, ${ displaystyle n geq 0}$, biz o'zboshimchalik bilan ro'yxat orqali juftliklar orasidagi masofani belgilay olamiz ${ displaystyle d_ {ij}> 0}$, ${ displaystyle 0 leq i$. Bu a ni belgilaydi semimetrik bo'shliq: metrik bo'shliq uchburchak tengsizligi.

Shubhasiz, biz semimetrik bo'shliqni bo'sh bo'lmagan to'plam sifatida aniqlaymiz ${ displaystyle R}$ semimetrik bilan jihozlangan ${ displaystyle d: R marta R dan [0, infty)}$ hamma uchun ${ displaystyle x, y in R}$,

1. Ijobiy: ${ displaystyle d (x, y) = 0}$ agar va faqat agar${ displaystyle x = y}$.
2. Simmetriya: ${ displaystyle d (x, y) = d (y, x)}$.

Har qanday metrik bo'shliq fortiori semimetrik bo'shliq. Jumladan, ${ displaystyle mathbb {R} ^ {k}}$, ${ displaystyle k}$- o'lchovli Evklid fazosi, bo'ladi kanonik masofa geometriyasidagi metrik bo'shliq.

Uchburchak tengsizligi ta'rifda chiqarib tashlangan, chunki biz masofalarga ko'proq cheklovlarni kiritishni xohlamaymiz. ${ displaystyle d_ {ij}}$ ularning ijobiy bo'lishi talabidan ko'ra.

Amalda semimetrik bo'shliqlar tabiiy ravishda noto'g'ri o'lchovlardan kelib chiqadi. Masalan, uchta ball berilgan ${ displaystyle A, B, C}$ chiziqda, bilan ${ displaystyle d_ {AB} = 1, d_ {BC} = 1, d_ {AC} = 2}$, noto'g'ri o'lchov berishi mumkin ${ displaystyle d_ {AB} = 0.99, d_ {BC} = 0.98, d_ {AC} = 2.00}$, uchburchak tengsizligini buzish.

Izometrik joylashtirish

Ikki semimetrik bo'shliq berilgan, ${ displaystyle (R, d), (R ', d')}$, an izometrik joylashish dan ${ displaystyle R}$ ga ${ displaystyle R '}$ xarita ${ displaystyle f: R dan R '}$ bu semimetrikni saqlaydi, ya'ni hamma uchun ${ displaystyle x, y in R}$, ${ displaystyle d (x, y) = d '(f (x), f (y))}$.

Masalan, cheklangan semimetrik bo'shliq berilgan ${ displaystyle (R, d)}$ Yuqorida belgilangan, izometrik joylashish nuqtalar bilan belgilanadi ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n} in { displaystyle mathbb {R} ^ {k}}}$, shu kabi ${ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ Barcha uchun ${ displaystyle 0 leq i$.

Afin mustaqilligi

Ballarni hisobga olgan holda ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n} in { displaystyle mathbb {R} ^ {k}}}$, ular aniqlangan affinely mustaqil, agar ular bitta korpusga sig'masa ${ displaystyle l}$ning o'lchovli affinali subspace ${ displaystyle mathbb {R} ^ {k}}$, har qanday kishi uchun ${ displaystyle l$, agar ${ displaystyle n}$-oddiy ular tarqaladi, ${ displaystyle v_ {n}}$, ijobiy ${ displaystyle n}$- hajm, ya'ni ${ displaystyle Vol_ {n} (v_ {n})> 0}$.

Umuman olganda, qachon ${ displaystyle k geq n}$, ular affinely mustaqil, chunki a umumiy n-simpleks noaniq. Masalan, tekislikdagi 3 nuqta, umuman olganda, kollinear emas, chunki ular uchburchak chiziqli bo'lakka aylanmaydi. Xuddi shunday, kosmosdagi 4 nuqta, umuman olganda, bir tekislik emas, chunki ular qamrab olgan tetraedr tekis uchburchakka aylanmaydi.

Qachon ${ displaystyle n> k}$, ular affinely qaram bo'lishi kerak. Buni har qanday ekanligini ta'kidlash orqali ko'rish mumkin ${ displaystyle n}$- ichiga sig‘adigan oddiy ${ displaystyle mathbb {R} ^ {k}}$ "tekis" bo'lishi kerak.

Ceyley-Menger determinantlari

Ceyley-Menger determinantlari, Artur Keyli va Karl Menger nomlari, nuqta to'plamlari orasidagi masofalar matritsalarining determinantlari hisoblanadi.

Ruxsat bering ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n}}$ bo'lishi n Semimetrik bo'shliqda + 1 ball, ularning Keyli-Menger determinantlari quyidagicha aniqlanadi

${ displaystyle CM (A_ {0}, cdots, A_ {n}) = { begin {vmatrix} 0 & d_ {01} ^ {2} & d_ {02} ^ {2} & cdots & d_ {0n} ^ { 2} & 1 d_ {01} ^ {2} & 0 & d_ {12} ^ {2} & cdots & d_ {1n} ^ {2} & 1 d_ {02} ^ {2} & d_ {12} ^ {2 } & 0 & cdots & d_ {2n} ^ {2} & 1 vdots & vdots & vdots & ddots & vdots & vdots d_ {0n} ^ {2} & d_ {1n} ^ {2} & d_ {2n} ^ {2} & cdots & 0 & 1 1 & 1 & 1 & cdots & 1 & 0 end {vmatrix}}}$

Agar ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n} in { displaystyle mathbb {R} ^ {k}}}$, keyin ular vertikallarni tashkil qiladi (ehtimol buzilib ketgan) n-oddiy ${ displaystyle { displaystyle v_ {n}}}$ yilda ${ displaystyle mathbb {R} ^ {k}}$. Buni ko'rsatish mumkin^[6] simpleksning n o'lchovli hajmi ${ displaystyle { displaystyle v_ {n}}}$ qondiradi

${ displaystyle Vol_ {n} (v_ {n}) ^ {2} = { frac {(-1) ^ {n + 1}} {(n!) ^ {2} 2 ^ {n}}} CM (A_ {0}, cdots, A_ {n})}$.

E'tibor bering, masalan uchun ${ displaystyle n = 0}$, bizda ... bor ${ displaystyle Vol_ {0} (v_ {0}) = 1}$, 0-simpleksning "0 o'lchovli hajmi" degan ma'noni anglatadi 1, ya'ni 0-simpleksda 1 nuqta mavjud.

${ textstyle A_ {0}, A_ {1}, ldots, A_ {n}}$ iffinely mustaqil ${ displaystyle Vol_ {n} (v_ {n})> 0}$, anavi, ${ displaystyle (-1) ^ {n + 1} CM (A_ {0}, cdots, A_ {n})> 0}$. Shunday qilib, Ceyley-Menger determinantlari afin mustaqilligini isbotlash uchun hisoblash usulini beradi.

Agar ${ displaystyle k$, keyin ballar affinely bog'liq bo'lishi kerak, shuning uchun ${ displaystyle CM (A_ {0}, cdots, A_ {n}) = 0}$. Keylining 1841 yilgi maqolasida maxsus holat o'rganilgan ${ displaystyle k = 3, n = 4}$, ya'ni har qanday 5 ball ${ displaystyle A_ {0}, cdots, A_ {5}}$ 3 o'lchovli kosmosda bo'lishi kerak ${ displaystyle CM (A_ {0}, cdots, A_ {4}) = 0}$.

Tarix

Masofa geometriyasidagi birinchi natija Heron formulasi, milodiy 1 asrdan boshlab, bu uchburchakning maydonini uning 3 ta uchi orasidagi masofadan beradi. Braxmagupta formulasi, milodiy VII asrdan boshlab, uni umumlashtiradi tsiklik to'rtburchaklar. Tartalya, milodiy 16-asrdan boshlab uni berish uchun umumlashtirgan tetraedrning hajmi uning 4 tepasi orasidagi masofadan.

Masofa geometriyasining zamonaviy nazariyasi boshlandi Authur Cayley va Karl Menger.^[7] Ceyley 1841 yilda Cayley determinantini nashr etdi,^[8] bu umumiy Keyli-Menger determinantining alohida hodisasidir. Menger 1928 yilda izometrik ravishda joylashtiriladigan barcha semimetrik bo'shliqlarning xarakteristikasi teoremasini isbotladi. n- o'lchovli Evklid fazosi ${ displaystyle mathbb {R} ^ {n}}$.^[9][10] 1931 yilda Menger Evklid geometriyasiga aksiomatik ishlov berish uchun masofaviy munosabatlarni qo'llagan.^[11]

Leonard Blumenthalkitobi^[12] bitiruv darajasida masofa geometriyasi uchun umumiy nuqtai nazarni taqdim etadi, ularning katta qismi nashr etilganidan keyin birinchi marta ingliz tilida davolanadi.

Menger xarakteristikasi teoremasi

Menger quyidagilarni isbotladi tavsiflash teoremasi semimetrik bo'shliqlar:^[2]

Semimetrik bo'shliq ${ displaystyle (R, d)}$ ga izometrik ravishda joylashtiriladi ${ displaystyle n}$- o'lchovli Evklid fazosi ${ displaystyle mathbb {R} ^ {n}}$, lekin emas ${ displaystyle mathbb {R} ^ {m}}$ har qanday kishi uchun ${ displaystyle 0 leq m$, agar va faqat:

1. ${ displaystyle R}$ o'z ichiga oladi ${ displaystyle (n + 1)}$- nuqta kichik to'plami ${ displaystyle S}$ bu izometrik, afinaviy mustaqil ${ displaystyle (n + 1)}$-ko’rsatkichli ichki qism ${ displaystyle mathbb {R} ^ {n}}$;
2. har qanday ${ displaystyle (n + 3)}$- nuqta kichik to'plami ${ displaystyle S '}$, ning har qanday ikkita qo'shimcha nuqtasini qo'shish orqali olinadi ${ displaystyle R}$ ga ${ displaystyle S}$, bilan mos keladi ${ displaystyle (n + 3)}$-ko’rsatkichli pastki qismi ${ displaystyle mathbb {R} ^ {n}}$.

Ushbu teoremaning biroz zaiflashgan shaklda isboti (semimetrik bo'shliqlar o'rniga metrik bo'shliqlar uchun).^[13]

Cayley-Menger determinantlari orqali tavsiflash

Quyidagi natijalar Blumetalning kitobida isbotlangan.^[12]

O'rnatish ${ displaystyle n + 1}$ ball ${ displaystyle mathbb {R} ^ {n}}$

Semimetrik bo'shliq berilgan ${ displaystyle (S, d)}$ , bilan ${ displaystyle S = {P_ {0}, cdots, P_ {n} }}$va ${ displaystyle d (P_ {i}, P_ {j}) = d_ {ij} geq 0}$, ${ displaystyle 0 leq i$, ning izometrik joylashtirilishi ${ displaystyle (S, d)}$ ichiga ${ displaystyle mathbb {R} ^ {n}}$ bilan belgilanadi ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n} in { displaystyle mathbb {R} ^ {n}}}$, shu kabi ${ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}}$ Barcha uchun ${ displaystyle 0 leq i$.

Shunga qaramay, bunday izometrik ko'milish mavjudmi yoki yo'qmi deb so'raydi ${ displaystyle (S, d)}$.

Kerakli shartni ko'rish oson: hamma uchun ${ displaystyle k = 1, cdots, n}$, ruxsat bering ${ displaystyle v_ {k}}$ bo'lishi ktomonidan tashkil etilgan-sodda ${ textstyle A_ {0}, A_ {1}, ldots, A_ {k}}$, keyin

${ displaystyle (-1) ^ {k + 1} CM (P_ {0}, cdots, P_ {k}) = (- 1) ^ {k + 1} CM (A_ {0}, cdots, A_ {k}) = 2 ^ {k} (k!) ^ {k} Vol_ {k} (v_ {k}) ^ {2} geq 0}$

Shuningdek, teskari tomon ham saqlanadi. Ya'ni, agar hamma uchun bo'lsa ${ displaystyle k = 1, cdots, n}$,

${ displaystyle (-1) ^ {k + 1} CM (P_ {0}, cdots, P_ {k}) geq 0}$,

unda bunday joylashtirish mavjud.

Bundan tashqari, bunday joylashish izometriyada noyobdir ${ displaystyle mathbb {R} ^ {n}}$. Ya'ni, tomonidan belgilangan har qanday ikkita izometrik ko'milish berilgan ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n}}$va ${ textstyle A '_ {0}, A' _ {1}, ldots, A '_ {n}}$, izometriya mavjud (albatta yagona emas) ${ displaystyle T: mathbb {R} ^ {n} to mathbb {R} ^ {n}}$, shu kabi ${ displaystyle T (A_ {k}) = A '_ {k}}$ Barcha uchun ${ displaystyle k = 0, cdots, n}$. Bunday ${ displaystyle T}$ agar shunday bo'lsa va noyob bo'lsa noyobdir ${ displaystyle CM (P_ {0}, cdots, P_ {n}) neq 0}$, anavi, ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n}}$ affinely mustaqil.

O'rnatish ${ displaystyle n + 2}$ va ${ displaystyle n + 3}$ ochkolar

Agar ${ displaystyle n + 2}$ ochkolar ${ displaystyle P_ {0}, cdots, P_ {n + 1}}$ ichiga joylashtirilishi mumkin ${ displaystyle mathbb {R} ^ {n}}$ kabi ${ displaystyle A_ {0}, cdots, A_ {n + 1}}$, keyin yuqoridagi shartlardan tashqari, qo'shimcha zarur shart bu ${ displaystyle (n + 1)}$tomonidan tashkil etilgan-sodda ${ textstyle A_ {0}, A_ {1}, ldots, A_ {n + 1}}$, yo'q bo'lishi kerak ${ displaystyle (n + 1)}$- o'lchov hajmi. Anavi, ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}) = 0}$.

Shuningdek, teskari tomon ham saqlanadi. Bu, agar hamma uchun bo'lsa ${ displaystyle k = 1, cdots, n}$,

${ displaystyle (-1) ^ {k + 1} CM (P_ {0}, cdots, P_ {k}) geq 0}$,

va

${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}) = 0}$,

unda bunday joylashtirish mavjud.

Joylashtirish uchun ${ displaystyle n + 3}$ ball ${ displaystyle mathbb {R} ^ {n}}$, zarur va etarli shartlar o'xshash:

1. Barcha uchun ${ displaystyle k = 1, cdots, n}$, ${ displaystyle (-1) ^ {k + 1} CM (P_ {0}, cdots, P_ {k}) geq 0}$;
2. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}) = 0}$;
3. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 2}) = 0}$;
4. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$.

O'zboshimchalik bilan ko'plab fikrlarni kiritish

The ${ displaystyle n + 3}$ umuman olganda etarli.

Umuman olganda, semimetrik bo'shliq berilgan ${ displaystyle (R, d)}$, u izometrik ravishda joylashtirilgan bo'lishi mumkin ${ displaystyle mathbb {R} ^ {n}}$ agar mavjud bo'lsa ${ displaystyle P_ {0}, cdots, P_ {n} in R}$, shunday qilib, hamma uchun ${ displaystyle k = 1, cdots, n}$, ${ displaystyle (-1) ^ {k + 1} CM (P_ {0}, cdots, P_ {k}) geq 0}$va har qanday kishi uchun ${ displaystyle P_ {n + 1}, P_ {n + 2} in R}$,

1. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}) = 0}$;
2. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 2}) = 0}$;
3. ${ displaystyle CM (P_ {0}, cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}$.

Va bunday joylashish izometriyada noyobdir ${ displaystyle mathbb {R} ^ {n}}$.

Bundan tashqari, agar ${ displaystyle CM (P_ {0}, cdots, P_ {n}) neq 0}$, keyin uni izometrik ravishda biron bir joyga singdirib bo'lmaydi ${ displaystyle mathbb {R} ^ {m}, m$. Va bunday joylashish noyob izometriyada noyobdir ${ displaystyle mathbb {R} ^ {n}}$.

Shunday qilib, Ceyley-Menger determinantlari semimetrik bo'shliqni ichiga kiritish mumkinligini hisoblashning aniq usulini beradi. ${ displaystyle mathbb {R} ^ {n}}$, ba'zi bir cheklanganlar uchun ${ displaystyle n}$va agar shunday bo'lsa, minimal nima bo'ladi ${ displaystyle n}$.

Ilovalar

Masofaviy geometriyaning ko'plab qo'llanmalari mavjud.^[3]

Kabi telekommunikatsiya tarmoqlarida GPS, ba'zi datchiklarning pozitsiyalari ma'lum (ular langar deb ataladi) va datchiklar orasidagi ba'zi masofalar ham ma'lum: muammo barcha datchiklar uchun pozitsiyalarni aniqlashda.^[5] Giperbolik navigatsiya GPSdan oldingi texnologiyadir, bu signallarni langarga etib borish vaqtiga qarab kemalarni topish uchun masofa geometriyasidan foydalanadi.

Kimyo fanida ko'plab dasturlar mavjud.^[4][12] Kabi usullar NMR berilgan molekulaning juft atomlari orasidagi masofani o'lchashi mumkin va muammo shu masofalardan molekulaning 3 o'lchovli shakli haqida xulosa chiqarishdir.

Ilovalar uchun ba'zi dasturiy ta'minot to'plamlari:

• DGSOL. Katta masofadagi geometriya masalalarini echadi makromolekulyar modellashtirish.
• Xplor-NIH. Asoslangan X-PLOR, NMR tajribalari ma'lumotlari asosida molekulalarning tuzilishini aniqlash. Masofaviy geometriya masalalarini evristik usullar bilan hal qiladi (masalan Simulyatsiya qilingan tavlanish) va mahalliy qidirish usullari (masalan Gradientni minimallashtirishni birlashtiring).
• TINKER. Molekulyar modellashtirish va loyihalash. Bu masofa geometriyasi muammolarini hal qilishi mumkin.
• SNLSDPclique. Datchiklar orasidagi masofadan kelib chiqqan holda datchiklar tarmog'idagi datchiklarni joylashtirish uchun MATLAB kodi.

Shuningdek qarang

• Evklid masofasi matritsasi
• Ko'p o'lchovli masshtablash (masofalar tasodifiy xatolar bilan o'lchanganida ishlatiladigan statistik usul)
• Metrik bo'shliq
• Tartaliyaning formulasi
• Uchburchak
• Trilateratsiya

Adabiyotlar