WikiDer > Ajoyib duoantiprizm

Great duoantiprism
Ajoyib duoantiprizm
TuriYagona polikron
Schläfli belgilar{5} s {5/3}
{5}⊗{5/3}
h {10} s {5/3}
s {5} soat {10/3}
soat {10} soat {10/3}
Kokseter diagrammasiCDel tugun h.pngCDel 5.pngCDel tugun h.pngCDel 2x.pngCDel tugun h.pngCDel 5.pngCDel rat.pngCDel 3x.pngCDel tugun h.png
CDel node.pngCDel 10.pngCDel tugun h.pngCDel 2x.pngCDel tugun h.pngCDel 5.pngCDel rat.pngCDel 3x.pngCDel tugun h.png
CDel tugun h.pngCDel 5.pngCDel tugun h.pngCDel 2x.pngCDel tugun h.pngCDel 10.pngCDel rat.pngCDel 3x.pngCDel node.png
CDel node.pngCDel 10.pngCDel tugun h.pngCDel 2x.pngCDel tugun h.pngCDel 10.pngCDel rat.pngCDel 3x.pngCDel node.png
Hujayralar50 (3.3.3) Tetrahedron.png
10 (3.3.3.5)Pentagonal antiprism.png
10 (3.3.3.5/3)Pentagrammik kesib o'tgan antiprizm.png
Yuzlar200 {3}
10 {5}
10 {5/2}
Qirralar200
Vertices50
Tepalik shakli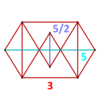Buyuk duoantiprizm verf.png
Yulduz-gyrobifastigium
Simmetriya guruhi[5,2,5]+, buyurtma 50
[(5,2)+, 10], 100 buyurtma
[10,2+, 10], 200 ga buyurtma bering
XususiyatlariVertex bir xil
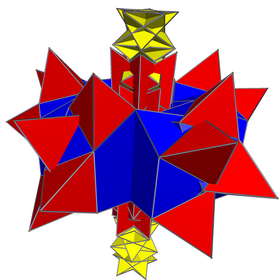Ajoyib duoantiprizm net.png
Tarmoq (kosmosda bir-biriga o'xshash)

The buyuk duoantiprizm yagona bir xil Yulduz-duoantiprizm p = 5, q = 5/3, ichida 4 o'lchovli geometriya. Unda bor Schläfli belgisi {5} ⊗ {5/3}, s {5} s {5/3} yoki ht0,1,2,3{5,2,5/3}, Kokseter diagrammasi CDel tugun h.pngCDel 5.pngCDel tugun h.pngCDel 2x.pngCDel tugun h.pngCDel 5.pngCDel rat.pngCDel 3x.pngCDel tugun h.png, 10 dan qurilgan beshburchak antiprizmalar, 10 pentagrammik o'zaro faoliyat antiprizmalarva 50 tetraedra.

Uning tepaliklari kichik hujayrali 120 hujayrali.

Qurilish

Katta duoantiprizmni 10-10 / 3 duoprizmning bir xil bo'lmagan variantidan qurish mumkin (a duoprizmi dekagon va a dekagramma) bu erda dekagrammaning chekka uzunligi 1.618 atrofida (oltin nisbat) an orqali dekagonning chekka uzunligidan kattaroq almashinish jarayon. The dekagonal prizmalar ichiga almashtirish beshburchak antiprizmalar, dekagrammatik prizmalar ichiga almashtirish pentagrammik o'zaro faoliyat antiprizmalar yangi muntazam bilan tetraedra o'chirilgan tepalarda yaratilgan. Bu p-q duoantiprizmi uchun odatdagidan tashqari yagona yagona echim 16 hujayradan iborat (2-2 duoantiprizm sifatida).

Tasvirlar

Ajoyib duoantiprism.png
stereografik proektsiya, bitta pentagrammik xoch-antiprizmga asoslangan		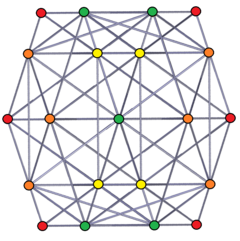Gudap ortogonal projection.png
Ortogonal proektsiya, qizil, to'q sariq, sariq, yashil ranglarning tepaliklari bir-birining ustiga o'ralgan holda 1, 2, 3,4 ga ko'paytiriladi.

Boshqa ismlar

  • Ajoyib duoantiprizm (gudap) Jonathan Bowers [1][2]

Adabiyotlar

  1. ^ Jonathan Bowers - Turli xil uniforma Polychora 965. Gudap
  2. ^ http://www.polychora.com/12GudapsMovie.gif Kesmalarning animatsiyasi
  • Muntazam Polytopes, H. S. M. Kokseter, Dover Publications, Inc., 1973, Nyu-York, p. 124.
  • Norman Jonson Yagona politoplar, Qo'lyozma (1991)
    • N.V. Jonson: Yagona politoplar va asal qoliplari nazariyasi, T.f.n. Dissertatsiya, Toronto universiteti, 1966 y
  • Klitzing, Richard. "4D yagona politoplari (polychora) s5 / 3s2s5s - gudap".