WikiDer > Giper to'rtburchak

Hyperrectangle
Giper to'rtburchak
n-ortotop
To'rtburchak kuboid
To'rtburchak kubik 3-ortotopdir
TuriPrizma
Yuzlari2n
Vertices2n
Schläfli belgisi{} × {} ... × {}[1]
Kokseter-Dinkin diagrammasiCDel tugun 1.pngCDel 2.pngCDel tugun 1.png ... CDel tugun 1.png
Simmetriya guruhi[2n−1], 2-buyurtman
Ikki tomonlamaTo'rtburchaklar n-fusil
Xususiyatlariqavariq, zonoedr, izogonal

Yilda geometriya, an n-ortotop[2] (shuningdek, a giper to'rtburchak yoki a quti) a-ning umumlashtirilishi to'rtburchak sifatida rasmiy ravishda belgilangan yuqori o'lchamlar uchun Dekart mahsuloti ning intervallar.

Turlari

Uch o'lchovli ortotop shuningdek, to'g'ri to'rtburchaklar deyiladi prizma, to'rtburchaklar kubikyoki to'rtburchaklar parallelepiped.

Maxsus holat n-ortotop, bu erda barcha qirralarning uzunligi teng bo'ladi n-kub.[2]

O'xshatishga ko'ra, "giper to'rtburchak" yoki "quti" atamasi kartezyen mahsulotlarini anglatadi ortogonal boshqa turdagi intervallar, masalan, tugmalar oralig'i ma'lumotlar bazasi nazariyasi yoki diapazonlari butun sonlar, dan ko'ra haqiqiy raqamlar.[3]

Ikki tomonlama politop

n-fusil
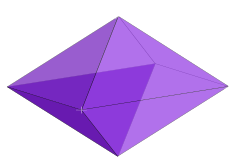To'rtburchak fuzil
Misol: 3-fusil
Yuzlari2n
Vertices2n
Schläfli belgisi{} + {} + ... + {}
Kokseter-Dinkin diagrammasiCDel tugun 1.pngCDel sum.pngCDel tugun 1.pngCDel sum.png ... CDel sum.pngCDel tugun 1.png
Simmetriya guruhi[2n−1], 2-buyurtman
Ikki tomonlaman-ortotop
Xususiyatlariqavariq, izotopal

The er-xotin politop ning n-ortotop turli xil to'rtburchaklar n- deb nomlanganortoppleks, rombik n-fusil, yoki n-pastil. U 2 tomonidan qurilgann ortotopning to'rtburchaklar yuzlari markazida joylashgan nuqtalar.

An n-fusilnikidir Schläfli belgisi yig‘indisi bilan ifodalanishi mumkin n ortogonal chiziq segmentlari: {} + {} + ... + {}.

1-fusil - bu a chiziqli segment. 2-fusil - bu a romb. Uning barcha juft o'qlaridagi tekis tekis o'zaro faoliyat tanlovlari rombi.

nNamunaviy rasm
1O'zaro faoliyat grafik 1.svg
{ }
CDel tugun 1.png
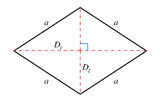2Romb (ko'pburchak) .png
{ } + { }
CDel tugun 1.pngCDel sum.pngCDel tugun 1.png
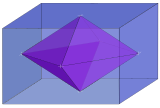3Ikki tomonlama ortotop-orthopleks.svg
Ichkarida rombik 3-ortoppleks 3-ortotop
{ } + { } + { }
CDel tugun 1.pngCDel sum.pngCDel tugun 1.pngCDel sum.pngCDel tugun 1.png

Shuningdek qarang

Izohlar

  1. ^ N.V. Jonson: Geometriyalar va transformatsiyalar, (2018) ISBN 978-1-107-10340-5 11-bob: Cheklangan simmetriya guruhlari, 11.5 Sferik kokseter guruhlari, 255-bet
  2. ^ a b Kokseter, 1973 yil
  3. ^ Masalan, qarang. Chjan, Yi; Munagala, Kamesh; Yang, iyun (2011), "Matritsalarni diskda saqlash: nazariya va amaliyot qayta ko'rib chiqildi" (PDF), Proc. VLDB, 4 (11): 1075–1086.

Adabiyotlar

Tashqi havolalar