WikiDer > Qadoqlash doimiyligi ma'lum bo'lgan shakllar ro'yxati
The qadoqlash doimiy geometrik jismning qadoqlash tartibida erishilgan eng katta o'rtacha zichligi uyg'un tananing nusxalari. Ko'pgina jismlar uchun qadoqlash konstantasining qiymati noma'lum.[1] Quyida, o'rash konstantasi ma'lum bo'lgan Evklid bo'shliqlaridagi jismlarning ro'yxati keltirilgan.[1] Fejes Tóth samolyotda, a ekanligini isbotladi nuqta nosimmetrik tanada unga teng bo'lgan qadoqlash konstantasi mavjud tarjima qadoqlash sobit va uning panjara qadoqlash doimiy.[2] Shuning uchun panjara qadoqlash konstantasi ilgari ma'lum bo'lgan har qanday bunday tanasi, masalan ellips, shuning uchun ma'lum qadoqlash doimiysi mavjud. Ushbu korpuslardan tashqari, ning qadoqlash konstantalari giperferalar 8 va 24 o'lchovlarda deyarli aniq ma'lum.[3]
| Rasm | Tavsif | Hajmi | Paket doimiy | Izohlar |
|---|---|---|---|---|
| Barcha shakllar kafel bo'sh joy | barchasi | 1 | Ta'rif bo'yicha | |
| Doira, Ellips | 2 | π/√12 ≈ 0.906900 | Dalil Thue[4] | |
| To'g'ri sakkizburchak | 2 | Reyxardt[5] | ||
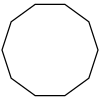
| Barcha 2 barobar nosimmetrik qavariq ko'pburchaklar | 2 | Lineer vaqt (vertikallar sonida) algoritmi tomonidan berilgan Tog' va Rut Silverman[6] | ||
| Sfera | 3 | π/√18 ≈ 0.7404805 | Qarang Kepler gumoni | |
| Ikki cheksiz silindr | 3 | π/√12 ≈ 0.906900 | Bezdek va Kuperberg[7] | |
| A tarkibidagi barcha shakllar rombik dodekaedr shaklida yozilgan shar shaklida bo'ladi | 3 | Hajmining fraktsiyasi rombik dodekaedr shakli bilan to'ldirilgan | Xulosa Kepler gumoni. Rasmdagi misollar: rombikuboktaedr va rombik enneakontaedr. | |
| Giperfera | 8 | Qarang Giperfera mahsuloti[8][9] | ||
| Giperfera | 24 | Qarang Giperfera mahsuloti |
Adabiyotlar
- ^ a b Bezdek, Andras; Kuperberg, Wlodzimierz (2010). "Har xil konveks qattiq moddalar bilan bo'shliqni zich qadoqlash". arXiv:1008.2398v1 [math.MG].
- ^ Fejes Toth, Laslo (1950). "Ba'zi qadoqlash va qoplash teoremalari". Acta Sci. Matematika. Seged. 12.
- ^ Kon, Genri; Kumar, Abhinav (2009). "Suluklar panjarasining panjaralar orasidagi optimalligi va o'ziga xosligi". Matematika yilnomalari. 170 (3): 1003–1050. arXiv:math.MG/0403263. doi:10.4007 / annals.2009.170.1003.
- ^ Chang, Xay-Chau; Vang, Lih-Chung (2010). "Dumaloq qadoqlash bo'yicha Thue teoremasining oddiy isboti". arXiv:1009.4322v1 [math.MG].
- ^ Reyxardt, Karl (1934). "Über die dichteste gitterförmige Lagerung kongruente Bereiche in der Ebene und eine besondere Art konvexer Kurven". Abh. Matematika. Sem. Univ. Gamburg. 10: 216–230. doi:10.1007 / bf02940676.
- ^ Mount, Devid M.; Silverman, Rut (1990). "Samolyotni qadoqlash va qavariq ko'pburchak tarjimasi bilan qoplash". Algoritmlar jurnali. 11 (4): 564–580. doi:10.1016 / 0196-6774 (90) 90010-C.
- ^ Bezdek, Andras; Kuperberg, Wlodzimierz (1990). "Cheksiz uzunlikdagi konversentli dumaloq silindrli maksimal zichlikdagi kosmik qadoqlash". Matematika. 37: 74–80. doi:10.1112 / s0025579300012808.
- ^ Klarreyx, Erika (2016 yil 30 mart), "Sfera qadoqlash katta o'lchamlarda hal qilindi", Quanta jurnali
- ^ Viazovska, Maryna (2016). "8 o'lchovdagi sharni qadoqlash muammosi". Matematika yilnomalari. 185 (3): 991–1015. arXiv:1603.04246. doi:10.4007 / annals.2017.185.3.7.