WikiDer > Matsubara chastotasi - Vikipediya

Bu maqola katta yoki to'liq bitta singari narsaga tayanadi manba. Iltimos yordam bering ushbu maqolani yaxshilang tanishtirish orqali iqtiboslar qo'shimcha manbalarga. Manbalarni toping: "Matsubara chastotasi" – Yangiliklar · gazetalar · kitoblar · olim · JSTOR (2011 yil sentyabr)

Yilda termal kvant maydon nazariyasi, Matsubara chastotasi yig'ish (nomi bilan Takeo Matsubara) diskret xayoliy chastotalar bo'yicha yig'indisidir. U quyidagi shaklni oladi

${ displaystyle S _ { eta} = { frac {1} { beta}} sum _ {i omega _ {n}} g (i omega _ {n}),}$

qayerda ${ displaystyle beta = hbar / k_ {B} T}$ teskari harorat va chastotalar ${ displaystyle omega _ {n}}$ odatda quyidagi ikkita to'plamning birortasidan olinadi (bilan ${ displaystyle n in mathbb {Z}}$):

bosonik chastotalar: ${ displaystyle omega _ {n} = { frac {2n pi} { beta}},}$

fermion chastotalar: ${ displaystyle omega _ {n} = { frac {(2n + 1) pi} { beta}},}$

Agar yig'indisi birlashadi ${ displaystyle g (z = i omega)}$ 0 ga intiladi ${ displaystyle z to infty}$ ga nisbatan tezroq cheklash ${ displaystyle z ^ {- 1}}$. Bosonik chastotalar bo'yicha yig'indisi quyidagicha belgilanadi ${ displaystyle S_ {B}}$ (bilan ${ displaystyle eta = + 1}$), fermion chastotalar ustidan esa quyidagicha belgilanadi ${ displaystyle S_ {F}}$ (bilan ${ displaystyle eta = -1}$). ${ displaystyle eta}$ bu statistik belgidir.

Matsubara chastotasini yig'ish usuli termal kvant maydon nazariyasidan tashqari, qattiq jismlar fizikasiga diagrammada yondoshishda ham muhim rol o'ynaydi, ya'ni diagrammalarni cheklangan haroratda ko'rib chiqilsa.^[1][2]

Umuman aytganda, agar bo'lsa ${ displaystyle T = 0 , { text {K}}}$, aniq Feynman diagrammasi integral bilan ifodalanadi ${ displaystyle int _ {T = 0} mathrm {d} omega g ( omega)}$, cheklangan haroratda u yig'indisi bilan beriladi ${ displaystyle S _ { eta}}$.

Matsubara chastotasini yig'ish

Umumiy rasmiylik

Shakl 1.

Shakl 2.

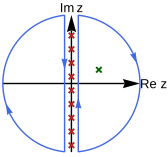
Matsubara chastotasi yig'indisini baholash uchun hiyla - Matsubara tortish funktsiyasidan foydalanish h_η(z) bu oddiy qutblar aniq joylashgan ${ displaystyle z = i omega}$. Boson holatidagi tortish funktsiyalari η = +1 va fermion ishi η = -1 farq qiladi. Og'irlik funktsiyasini tanlash keyinroq muhokama qilinadi. Tortish funktsiyasi bilan summani xayoliy o'qni o'rab turgan kontur integral bilan almashtirish mumkin.

${ displaystyle S _ { eta} = { frac {1} { beta}} sum _ {i omega} g (i omega) = { frac {1} {2 pi i beta}} oint g (z) h _ { eta} (z) , dz,}$

1-rasmda bo'lgani kabi, tortish funktsiyasi xayoliy o'qda qutblar (qizil xochlar) hosil qiladi. Konturning ajralmas qismi qoldiq bu qutblarning yig'indisiga teng.

Qutblarini o'rab olish uchun kontur chiziqlarining deformatsiyasi bilan g(z) (2-rasmdagi yashil xoch), summani rasmiy ravishda qoldiqni yig'ish yo'li bilan amalga oshirish mumkin g(z)h_η(z) barcha qutblar ustida g(z),

${ displaystyle S _ { eta} = - { frac {1} { beta}} sum _ {z_ {0} in g (z) { text {qutular}}} operatorname {Res} g ( z_ {0}) h _ { eta} (z_ {0}).}$

E'tibor bering, minus belgisi hosil bo'ladi, chunki qutblarni soat yo'nalishi bo'yicha yopish uchun kontur deformatsiyalanadi, natijada salbiy qoldiq paydo bo'ladi.

Matsubara vaznini aniqlash funktsiyasini tanlash

Boson chastotalarida oddiy qutblarni ishlab chiqarish ${ displaystyle z = i omega _ {n}}$, Matsubara vaznini tortish funktsiyalarining quyidagi ikki turidan birini tanlash mumkin

${ displaystyle h_ {B} ^ {(1)} (z) = { frac { beta} {1-e ^ {- beta z}}} = - beta n_ {B} (- z) = beta (1 + n_ {B} (z)),}$

${ displaystyle h_ {B} ^ {(2)} (z) = { frac {- beta} {1-e ^ { beta z}}} = beta n_ {B} (z),}$

yaqinlik qaysi yarim tekislikda boshqarilishi kerakligiga qarab. ${ displaystyle h_ {B} ^ {(1)} (z)}$ chap yarim tekislikdagi yaqinlashishni boshqaradi (Rez <0), esa ${ displaystyle h_ {B} ^ {(2)} (z)}$ o'ng yarim tekislikdagi yaqinlashishni boshqaradi (Rez > 0). Bu yerda ${ displaystyle n_ {B} (z) = (e ^ { beta z} -1) ^ {- 1}}$ bo'ladi Bose-Eynshteyn tarqatish funktsiyasi.

Ish fermion chastotalari uchun o'xshash. Matsubara tortish funktsiyalari ikki xil bo'lib, ular oddiy qutblarni ishlab chiqaradi ${ displaystyle z = i omega _ {m}}$

${ displaystyle h_ {F} ^ {(1)} (z) = { frac { beta} {1 + e ^ {- beta z}}} = beta n_ {F} (- z) = beta (1-n_ {F} (z)),}$

${ displaystyle h_ {F} ^ {(2)} (z) = { frac {- beta} {1 + e ^ { beta z}}} = - beta n_ {F} (z).}$

${ displaystyle h_ {F} ^ {(1)} (z)}$ chap yarim tekislikdagi yaqinlashishni boshqaradi (Rez <0), esa ${ displaystyle h_ {F} ^ {(2)} (z)}$ o'ng yarim tekislikdagi yaqinlashishni boshqaradi (Rez > 0). Bu yerda ${ displaystyle n_ {F} (z) = (e ^ { beta z} +1) ^ {- 1}}$ bo'ladi Fermi-Dirak tarqatish funktsiyasi.

Green funktsiyasini hisoblash uchun arizada, g(z) har doim tuzilishga ega

${ displaystyle g (z) = G (z) e ^ {- z tau},}$

0 τ < β. Konvergentsiyani boshqarish uchun har doim birinchi turdagi tortish funktsiyasi tanlanadi ${ displaystyle h _ { eta} (z) = h _ { eta} ^ {(1)} (z)}$. Biroq, Matsubara yig'indisi bir-biridan farq qilmasa, konvergentsiyani boshqarishga hojat yo'q, u holda Matsubara tortish funktsiyasini har qanday tanlovi bir xil natijalarga olib keladi.

Matsubara chastotasi yig'ilishlari jadvali

Quyidagi jadvalda Matsubara chastotasi yig'indisi ba'zi bir sodda so'zlar bilan yakunlanadi ratsional funktsiyalar g(z).

${ displaystyle S _ { eta} = { frac {1} { beta}} sum _ {i omega} g (i omega).}$

η = ± 1 statistik belgini belgilaydi.

${ displaystyle g (i omega)}$	${ displaystyle S _ { eta}}$
${ displaystyle (i omega - xi) ^ {- 1}}$	${ displaystyle - eta n _ { eta} ( xi)}$[1]
${ displaystyle (i omega - xi) ^ {- 2}}$	${ displaystyle - eta n _ { eta} ^ { prime} ( xi) = beta n _ { eta} ( xi) ( eta + n _ { eta} ( xi))}$
${ displaystyle (i omega - xi) ^ {- n}}$	${ displaystyle - { frac { eta} {(n-1)!}} qismli _ { xi} ^ {n-1} n _ { eta} ( xi)}$
${ displaystyle { frac {1} {(i omega - xi _ {1}) (i omega - xi _ {2})}}}$	${ displaystyle - { frac { eta (n _ { eta} ( xi _ {1}) - n _ { eta} ( xi _ {2}))} { xi _ {1} - xi _ {2}}}}$
${ displaystyle { frac {1} {(i omega - xi _ {1}) ^ {2} (i omega - xi _ {2}) ^ {2}}}}$	${ displaystyle { frac { eta} {( xi _ {1} - xi _ {2}) ^ {2}}} left ({ frac {2 (n _ { eta} ( xi _) {1}) - n _ { eta} ( xi _ {2}))} { xi _ {1} - xi _ {2}}} - (n _ { eta} ^ { prime} ( xi _ {1}) + n _ { eta} ^ { prime} ( xi _ {2})) o'ng)}$
${ displaystyle { frac {1} {(i omega - xi _ {1}) ^ {2} - xi _ {2} ^ {2}}}}$	${ displaystyle eta c _ { eta} ( xi _ {1}, xi _ {2})}$
${ displaystyle { frac {1} {(i omega) ^ {2} - xi ^ {2}}}}$	${ displaystyle eta c _ { eta} (0, xi) = - { frac {1} {2 xi}} (1 + 2 eta n _ { eta} ( xi))}$
${ displaystyle { frac {(i omega) ^ {2}} {(i omega) ^ {2} - xi ^ {2}}}}$	${ displaystyle - { frac { xi} {2}} (1 + 2 eta n _ { eta} ( xi))}$[1]
${ displaystyle { frac {1} {((i omega) ^ {2} - xi ^ {2}) ^ {2}}}}$	${ displaystyle - { frac { eta} {2 xi ^ {2}}} (c _ { eta} (0, xi) + n _ { eta} ^ { prime} ( xi))}$
${ displaystyle { frac {(i omega) ^ {2}} {((i omega) ^ {2} - xi ^ {2}) ^ {2}}}}$	${ displaystyle { frac { eta} {2}} (c _ { eta} (0, xi) -n _ { eta} ^ { prime} ( xi))}$
${ displaystyle { frac {(i omega) ^ {2} + xi ^ {2}} {((i omega) ^ {2} - xi ^ {2}) ^ {2}}}}$	${ displaystyle - eta n _ { eta} ^ { prime} ( xi) = beta n _ { eta} ( xi) ( eta + n _ { eta} ( xi))}$
${ displaystyle { frac {1} {((i omega) ^ {2} - xi _ {1} ^ {2}) ((i omega) ^ {2} - xi _ {2} ^) {2})}}}$	${ displaystyle { frac { eta (c _ { eta} (0, xi _ {1}) - c _ { eta} (0, xi _ {2}))} { xi _ {1} ^ {2} - xi _ {2} ^ {2}}}}$
${ displaystyle chap ({ frac {1} {(i omega) ^ {2} - xi _ {1} ^ {2}}} + { frac {1} {(i omega) ^ { 2} - xi _ {2} ^ {2}}} o'ng) ^ {2}}$	${ displaystyle eta left ({ frac {3 xi _ {1} ^ {2} + xi _ {2} ^ {2}} {2 xi _ {1} ^ {2} ( xi) _ {1} ^ {2} - xi _ {2} ^ {2})}} c _ { eta} (0, xi _ {1}) - { frac {n _ { eta} ^ { prime} ( xi _ {1})} {2 xi _ {1} ^ {2}}} o'ng) + (1 chap tomondagi o'q 2)}$[2]
${ displaystyle chap ({ frac {1} {(i omega) ^ {2} - xi _ {1} ^ {2}}} - { frac {1} {(i omega) ^ { 2} - xi _ {2} ^ {2}}} o'ng) ^ {2}}$	${ displaystyle eta left (- { frac {5 xi _ {1} ^ {2} - xi _ {2} ^ {2}} {2 xi _ {1} ^ {2} ( xi _ {1} ^ {2} - xi _ {2} ^ {2})}} c _ { eta} (0, xi _ {1}) - { frac {n _ { eta} ^ { prime} ( xi _ {1})} {2 xi _ {1} ^ {2}}} o'ng) + (1 chap tomondagi o'q 2)}$[2]

[1] Summa yaqinlashmagani uchun, Matsubara tortish funktsiyasini har xil tanlashda natija farq qilishi mumkin.

[2] (1-2) oldingi bilan bir xil ifodani bildiradi, lekin 1 va 2 indekslari almashtiriladi.

Fizikadan dasturlar

Nolinchi harorat chegarasi

Ushbu chegarada ${ displaystyle beta rightarrow infty}$, Matsubara chastotasi yig'indisi xayoliy chastota xayoliy o'qi bo'yicha integratsiyasiga tengdir.

${ displaystyle { frac {1} { beta}} sum _ {i omega} = int _ {- i infty} ^ {i infty} { frac { mathrm {d} (i omega)} {2 pi}}.}$

Ayrim integrallar yaqinlashmaydi. Ular chastotali uzilishni joriy qilish orqali tartibga solinishi kerak ${ displaystyle Omega}$va keyin ikkiga bo'linadigan qismni olib tashlang (${ displaystyle Omega}$chegarasini olishdan oldin integraldan) ${ displaystyle Omega rightarrow infty}$. Masalan, erkin energiya logarifm integrali bilan olinadi,

${ displaystyle eta lim _ { Omega rightarrow infty} left [ int _ {- i Omega} ^ {i Omega} { frac { mathrm {d} (i omega)} { 2 pi}} chap ( ln (-i omega + xi) - { frac { pi xi} {2 Omega}} o'ng) - { frac { Omega} { pi} } ( ln Omega -1) right] = left {{ begin {array} {cc} 0 & xi geq 0, - eta xi & xi <0, end {array }} o'ng.}$

ya'ni nol haroratda erkin energiya shunchaki kimyoviy potentsial ostidagi ichki energiya bilan bog'liq. Shuningdek tarqatish funktsiyasi quyidagi integral orqali olinadi

${ displaystyle eta lim _ { Omega rightarrow infty} int _ {- i Omega} ^ {i Omega} { frac { mathrm {d} (i omega)} {2 pi }} chap ({ frac {1} {- i omega + xi}} - { frac { pi} {2 Omega}} o'ng) = chap {{ begin {array} { cc} 0 & xi geq 0, - eta & xi <0, end {array}} right.}$

bu nol haroratda qadam funktsiyasi harakatini ko'rsatadi.

Yashilning vazifasi

Vaqt domeni

Funktsiyani ko'rib chiqing G(τ) xayoliy vaqt oralig'ida aniqlangan (0,β). Furye seriyasida berilishi mumkin,

${ displaystyle G ( tau) = { frac {1} { beta}} sum _ {i omega} G (i omega) e ^ {- i omega tau},}$

bu erda chastota faqat 2 oralig'idagi alohida qiymatlarni oladiπ/β.

Chastotani alohida tanlash funktsiyaning chegara holatiga bog'liq G(τ). Fizikada, G(τ) Green funktsiyasining xayoliy vaqt vakili degan ma'noni anglatadi

${ displaystyle G ( tau) = - langle { mathcal {T}} _ { tau} psi ( tau) psi ^ {*} (0) rangle.}$

U davriy chegara shartini qondiradi G(τ+β)=G(τ) boson maydoni uchun. Fermion maydoni uchun chegara holati davriydir G(τ + β) = −G(τ).

Yashilning funktsiyasini hisobga olgan holda G(iω) chastota domenida, uning xayoliy vaqt vakili G(τ) Matsubara chastotasi yig'indisi bilan baholanishi mumkin. Xulosa qilinadigan bozon yoki fermion chastotalariga qarab, natijada G(τ) har xil bo'lishi mumkin. Ajratish uchun aniqlang

${ displaystyle G _ { eta} ( tau) = { start {case} G_ {B} ( tau), & { text {if}} eta = + 1, G_ {F} ( tau), & { text {if}} eta = -1, end {case}}}$

bilan

${ displaystyle G_ {B} ( tau) = { frac {1} { beta}} sum _ {i omega _ {n}} G (i omega _ {n}) e ^ {- i omega _ {n} tau},}$

${ displaystyle G_ {F} ( tau) = { frac {1} { beta}} sum _ {i omega _ {m}} G (i omega _ {m}) e ^ {- i omega _ {m} tau}.}$

Yozib oling τ asosiy intervalda cheklangan (0,β). Chegaraviy shartni kengaytirish uchun foydalanish mumkin G(τ) asosiy intervaldan tashqari. Ba'zi tez-tez ishlatiladigan natijalar quyidagi jadvalda keltirilgan.

${ displaystyle G (i omega)}$	${ displaystyle G _ { eta} ( tau)}$
${ displaystyle (i omega - xi) ^ {- 1}}$	${ displaystyle -e ^ { xi ( beta - tau)} n _ { eta} ( xi)}$
${ displaystyle (i omega - xi) ^ {- 2}}$	${ displaystyle e ^ { xi ( beta - tau)} n _ { eta} ( xi) left ( tau + eta beta n _ { eta} ( xi) right)}$
${ displaystyle (i omega - xi) ^ {- 3}}$	${ displaystyle - { frac {1} {2}} e ^ { xi ( beta - tau)} n _ { eta} ( xi) left ( tau ^ {2} + eta beta ( beta +2 tau) n _ { eta} ( xi) +2 beta ^ {2} n _ { eta} ^ {2} ( xi) right)}$
${ displaystyle (i omega - xi _ {1}) ^ {- 1} (i omega - xi _ {2}) ^ {- 1}}$	${ displaystyle - { frac {e ^ { xi _ {1} ( beta - tau)} n _ { eta} ( xi _ {1}) - e ^ { xi _ {2} ( beta - tau)} n _ { eta} ( xi _ {2})} { xi _ {1} - xi _ {2}}}}$
${ displaystyle ( omega ^ {2} + m ^ {2}) ^ {- 1}}$	${ displaystyle { frac {e ^ {- m tau}} {2m}} + { frac { eta} {m}} cosh {m tau} ; n _ { eta} (m)}$
${ displaystyle i omega ( omega ^ {2} + m ^ {2}) ^ {- 1}}$	${ displaystyle { frac {e ^ {- m tau}} {2}} - eta , sinh {m tau} ; n _ { eta} (m)}$

Operatorni almashtirish effekti

Kichkina xayoliy vaqt bu erda hal qiluvchi rol o'ynaydi. Agar kichik xayoliy vaqt belgisi o'zgargan bo'lsa, operatorlarning tartibi o'zgaradi.

${ displaystyle langle psi psi ^ {*} rangle = langle { mathcal {T}} _ { tau} psi ( tau = 0 ^ {+}) psi ^ {*} (0 ) rangle = -G _ { eta} ( tau = 0 ^ {+}) = - { frac {1} { beta}} sum _ {i omega} G (i omega) e ^ { -i omega 0 ^ {+}}}$

${ displaystyle langle psi ^ {*} psi rangle = eta langle { mathcal {T}} _ { tau} psi ( tau = 0 ^ {-}) psi ^ {*} (0) rangle = - eta G _ { eta} ( tau = 0 ^ {-}) = - { frac { eta} { beta}} sum _ {i omega} G (i ) omega) e ^ {i omega 0 ^ {+}}}$

Tarqatish funktsiyasi

Tarqatish funktsiyasini baholash Grinning funktsiyasi to'xtab qolishi sababli hiyla-nayrangga aylanadi G(τ) da τ = 0. Summatni baholash uchun

${ displaystyle G (0) = sum _ {i omega} (i omega - xi) ^ {- 1},}$

tortish funktsiyasining ikkala tanlovi ham qabul qilinadi, ammo natijalar boshqacha. Agar biz itarsak, buni tushunish mumkin G(τ) uzoqda τ = 0 biroz, keyin konvergentsiyani boshqarish uchun biz olishimiz kerak ${ displaystyle h _ { eta} ^ {(1)} (z)}$ uchun tortish funktsiyasi sifatida ${ displaystyle G ( tau = 0 ^ {+})}$va ${ displaystyle h _ { eta} ^ {(2)} (z)}$ uchun ${ displaystyle G ( tau = 0 ^ {-})}$.

Bosonlar

${ displaystyle G_ {B} ( tau = 0 ^ {-}) = { frac {1} { beta}} sum _ {i omega _ {n}} { frac {e ^ {i omega _ {n} 0 ^ {+}}} {i omega _ {n} - xi}} = - n_ {B} ( xi),}$

${ displaystyle G_ {B} ( tau = 0 ^ {+}) = { frac {1} { beta}} sum _ {i omega _ {n}} { frac {e ^ {- i omega _ {n} 0 ^ {+}}} {i omega _ {n} - xi}} = - (n_ {B} ( xi) +1).}$

Fermionlar

${ displaystyle G_ {F} ( tau = 0 ^ {-}) = { frac {1} { beta}} sum _ {i omega _ {m}} { frac {e ^ {i omega _ {m} 0 ^ {+}}} {i omega _ {m} - xi}} = n_ {F} ( xi),}$

${ displaystyle G_ {F} ( tau = 0 ^ {+}) = { frac {1} { beta}} sum _ {i omega _ {m}} { frac {e ^ {- i omega _ {m} 0 ^ {+}}} {i omega _ {m} - xi}} = - (1-n_ {F} ( xi)).}$

Bepul energiya

Bosonlar

${ displaystyle { frac {1} { beta}} sum _ {i omega _ {n}} ln ( beta (-i omega _ {n} + xi)) = { frac { 1} { beta}} ln (1-e ^ {- beta xi}),}$

Fermionlar

${ displaystyle - { frac {1} { beta}} sum _ {i omega _ {m}} ln ( beta (-i omega _ {m} + xi)) = = - { frac {1} { beta}} ln (1 + e ^ {- beta xi}).}$

Diagrammalarni baholash

Bu erda tez-tez uchraydigan diagrammalar bitta rejim sozlamalari bilan baholanadi. Spektral funktsiya integrali yordamida bir nechta rejim masalasiga murojaat qilish mumkin.

Fermion o'z-o'zini energiya

${ displaystyle Sigma (i omega _ {m}) = - { frac {1} { beta}} sum _ {i omega _ {n}} { frac {1} {i omega _ {m} + i omega _ {n} - varepsilon}} { frac {1} {i omega _ {n} - Omega}} = { frac {n_ {F} ( varepsilon) -n_ {F} ( Omega)} {i omega _ {m} - varepsilon + Omega}}.}$

Zarrachalar teshik pufagi

${ displaystyle Pi (i omega _ {n}) = { frac {1} { beta}} sum _ {i omega _ {m}} { frac {1} {i omega _ { m} + i omega _ {n} - varepsilon}} { frac {1} {i omega _ {m} - varepsilon '}} = - { frac {n_ {F} ( varepsilon) - n_ {F} chap ( varepsilon ' o'ng)} {i omega _ {n} - varepsilon + varepsilon'}}.}$

Zarrachalar zarrachalari pufagi

${ displaystyle Pi (i omega _ {n}) = - { frac {1} { beta}} sum _ {i omega _ {m}} { frac {1} {i omega _ {m} + i omega _ {n} - epsilon}} { frac {1} {- i omega _ {m} - epsilon '}} = { frac {1-n_ {F} ( epsilon) -n_ {F} chap ( epsilon ' o'ng)} {i omega _ {n} - epsilon - epsilon'}}.}$

Ilova: Tarqatish funktsiyalarining xususiyatlari

Tarqatish funktsiyalari

Umumiy yozuv ${ displaystyle n _ { eta}}$ Bose (yokiη = +1) yoki Fermi (η = -1) tarqatish funktsiyasi

${ displaystyle n _ { eta} ( xi) = { frac {1} {e ^ { beta xi} - eta}}.}$

Agar kerak bo'lsa, aniq belgilar n_B va n_F Bose va Fermi tarqatish funktsiyalarini mos ravishda ko'rsatish uchun ishlatiladi

${ displaystyle n _ { eta} ( xi) = { begin {case} n_ {B} ( xi), & { text {if}} eta = + 1, n_ {F} ( xi), & { text {if}} eta = -1. end {case}}}$

Giperbolik funktsiyalar bilan aloqasi

Bose tarqatish funktsiyasi giperbolik kotangens funktsiyasi bilan bog'liq

${ displaystyle n_ {B} ( xi) = { frac {1} {2}} chap ( operatorname {coth} { frac { beta xi} {2}} - 1 right).}$

Fermining taqsimlash funktsiyasi giperbolik tangens funktsiyasi bilan bog'liq

${ displaystyle n_ {F} ( xi) = { frac {1} {2}} left (1- operatorname {tanh} { frac { beta xi} {2}} right).}$

Paritet

Ikkala tarqatish funktsiyalari aniq tenglikka ega emas,

${ displaystyle n _ { eta} (- xi) = - eta -n _ { eta} ( xi).}$

Boshqa formulalar ${ displaystyle c _ { eta}}$ funktsiya

${ displaystyle n _ { eta} (- xi) = n _ { eta} ( xi) +2 xi c _ { eta} (0, xi).}$

Ammo ularning hosilalari aniq tenglikka ega.

Bose-Fermi transmutatsiyasi

Bose va Fermi taqsimlash funktsiyalari o'zgaruvchan o'zgaruvchan fermion chastotasi ostida o'zgaradi,

${ displaystyle n _ { eta} (i omega _ {m} + xi) = - n _ {- eta} ( xi).}$

Biroq bosonik chastotalar bilan siljish hech qanday farq qilmaydi.

Hosilalari

Birinchi buyurtma

${ displaystyle n_ {B} ^ { prime} ( xi) = - { frac { beta} {4}} mathrm {csch} ^ {2} { frac { beta xi} {2} },}$

${ displaystyle n_ {F} ^ { prime} ( xi) = - { frac { beta} {4}} mathrm {sech} ^ {2} { frac { beta xi} {2} }.}$

Mahsulot jihatidan:

${ displaystyle n _ { eta} ^ { prime} ( xi) = - beta n _ { eta} ( xi) (1+ eta n _ { eta} ( xi)).}$

Nolinchi harorat chegarasida:

${ displaystyle n _ { eta} ^ { prime} ( xi) = eta delta ( xi) { text {as}} beta rightarrow infty.}$

Ikkinchi tartib

${ displaystyle n_ {B} ^ { prime prime} ( xi) = { frac { beta ^ {2}} {4}} operatorname {csch} ^ {2} { frac { beta xi} {2}} operator nomi {coth} { frac { beta xi} {2}},}$

${ displaystyle n_ {F} ^ { prime prime} ( xi) = { frac { beta ^ {2}} {4}} operatorname {sech} ^ {2} { frac { beta xi} {2}} operator nomi {tanh} { frac { beta xi} {2}}.}$

Farq formulasi

${ displaystyle n _ { eta} (a + b) -n _ { eta} (ab) = - { frac { mathrm {sinh} beta b} { mathrm {cosh} beta a- eta , mathrm {cosh} beta b}}.}$

Ish a = 0

${ displaystyle n_ {B} (b) -n_ {B} (- b) = mathrm {coth} { frac { beta b} {2}},}$

${ displaystyle n_ {F} (b) -n_ {F} (- b) = - mathrm {tanh} { frac { beta b} {2}}.}$

Ish a → 0

${ displaystyle n_ {B} (a + b) -n_ {B} (ab) = operatorname {coth} { frac { beta b} {2}} + n_ {B} ^ { prime prime} (b) a ^ {2} + cdots,}$

${ displaystyle n_ {F} (a + b) -n_ {F} (ab) = - operatorname {tanh} { frac { beta b} {2}} + n_ {F} ^ { prime prime } (b) a ^ {2} + cdots.}$

Ish b → 0

${ displaystyle n_ {B} (a + b) -n_ {B} (a-b) = 2n_ {B} ^ { prime} (a) b + cdots,}$

${ displaystyle n_ {F} (a + b) -n_ {F} (a-b) = 2n_ {F} ^ { prime} (a) b + cdots.}$

Funktsiya v_η

Ta'rif:

${ displaystyle c _ { eta} (a, b) equiv - { frac {n _ { eta} (a + b) -n _ { eta} (a-b)} {2b}}.}$

Bose va Fermi turlari uchun:

${ displaystyle c_ {B} (a, b) equiv c _ {+} (a, b),}$

${ displaystyle c_ {F} (a, b) equiv c _ {-} (a, b).}$

Giperbolik funktsiyalar bilan aloqasi

${ displaystyle c _ { eta} (a, b) = { frac { sinh beta b} {2b ( cosh beta a- eta cosh beta b)}}.}$

Bu aniq ${ displaystyle c_ {F} (a, b)}$ ijobiy aniq.

Raqamli hisoblashda toshib ketmaslik uchun tanh va coth funktsiyalari ishlatiladi

${ displaystyle c_ {B} (a, b) = { frac {1} {4b}} left ( operatorname {coth} { frac { beta (ab)} {2}} - operatorname {coth) } { frac { beta (a + b)} {2}} o'ng),}$

${ displaystyle c_ {F} (a, b) = { frac {1} {4b}} left ( operatorname {tanh} { frac { beta (a + b)} {2}} - operatorname {tanh} { frac { beta (ab)} {2}} o'ng).}$

Ish a = 0

${ displaystyle c_ {B} (0, b) = - { frac {1} {2b}} operatorname {coth} { frac { beta b} {2}},}$

${ displaystyle c_ {F} (0, b) = { frac {1} {2b}} operatorname {tanh} { frac { beta b} {2}}.}$

Ish b = 0

${ displaystyle c_ {B} (a, 0) = { frac { beta} {4}} operatorname {csch} ^ {2} { frac { beta a} {2}},}$

${ displaystyle c_ {F} (a, 0) = { frac { beta} {4}} operatorname {sech} ^ {2} { frac { beta a} {2}}.}$

Past harorat chegarasi

Uchun a = 0: ${ displaystyle c_ {F} (0, b) = { frac {1} {2 | b |}}.}$

Uchun b = 0: ${ displaystyle c_ {F} (a, 0) = delta (a).}$

Umuman,

${ displaystyle c_ {F} (a, b) = { begin {case} { frac {1} {2 | b |}}, & { text {if}} | a | <| b | 0, & { text {if}} | a |> | b | end {case}}}$

Shuningdek qarang

• Xayoliy vaqt
• Maydonlarning termal kvant nazariyasi

Tashqi havolalar

Agustin Nieto: Matsubara chastotalari bo'yicha yig'indilarni baholash. arXiv: hep-ph / 9311210

Github ombori: MatsubaraSum Matsubara chastotasini yig'ish uchun Mathematica to'plami.

A. Taheridehkordi, S. Kurno, J.P.F. LeBlanc: Xabardga o'xshash modellar uchun algoritmik Matsubara integratsiyasi.. arXiv: cond-mat / 1808.05188

Adabiyotlar