WikiDer > Qavariq bo'lmagan katta rombikuboktaedr

Nonconvex great rhombicuboctahedron

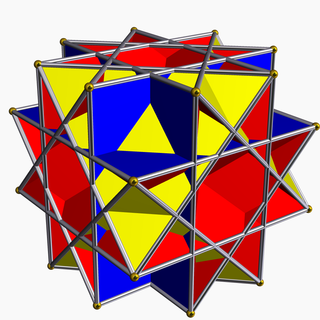
Qavariq bo'lmagan katta rombikuboktaedr

Turi	Yagona yulduzli ko'pburchak
Elementlar	F = 26, E = 48 V = 24 (χ = 2)
Yuzlar yonma-yon	8{3}+(6+12){4}
Wythoff belgisi	3/2 4 \| 2 3 4/3 \| 2
Simmetriya guruhi	O_h, [4,3], *432
Indeks ma'lumotnomalari	U₁₇, C₅₉, V₈₅
Ikki tomonlama ko'pburchak	Deltoidal ikozitetraedr
Tepalik shakli	4.4.4.3/2
Bowers qisqartmasi	Querco

Qavariq bo'lmagan katta rombikuboktaedrning 3D modeli

Yilda geometriya, konveks katta rombikuboktaedr a konveks bo'lmagan bir xil ko'pburchak, U sifatida indekslangan₁₇. Uning 26 yuzi bor (8 uchburchaklar va 18 kvadratchalar), 48 qirrasi va 24 ta tepasi.^[1] Bu bilan ifodalanadi Schläfli belgisi t_0,2{4,³⁄₂} va Kokseter-Dinkin diagrammasi ning . Uning tepalik shakli a kesib o'tgan to'rtburchak.

Ushbu model nomni konveks bilan baham ko'radi katta rombikuboktaedr, shuningdek kesilgan kuboktaedr.

Ushbu raqamning muqobil nomi kvasirombikuboktaedr. Shundan Bowers qisqartmasi kelib chiqadi: querco.

Ortogonal proektsiyalar

Dekart koordinatalari a tepaliklari uchun qavariq bo'lmagan katta rombikuboktaedr 1 ta chekka uzunligi bilan boshlangichning markazida joylashgan

(±ξ, ±1, ±1),

qayerda ξ = √2 − 1.

U ulashadi vertikal tartibga solish qavariq bilan kesilgan kub. U qo'shimcha ravishda o'z ulushini baham ko'radi chekka tartib bilan katta kububoktaedr (uchburchak yuzlari va 6 kvadrat yuzlari umumiy) va ular bilan ajoyib rombiheksaedr (umumiy 12 kvadrat yuzga ega). U xuddi xuddi vertikal shaklga ega psevdo buyuk rombikuboktaedr, bu bir xil ko'pburchak emas.

Qisqartirilgan kub	Ajoyib rombikuboktaedr	Ajoyib kububoktaedr	Rombiheksaedr ajoyib	Psevdo buyuk rombikuboktaedr

Deltoidal ikozitetraedr

Turi	Yulduzli ko'pburchak
Yuz
Elementlar	F = 24, E = 48 V = 26 (χ = 2)
Simmetriya guruhi	O_h, [4,3], *432
Indeks ma'lumotnomalari	DU₁₇
ikki tomonlama ko'pburchak	Qavariq bo'lmagan katta rombikuboktaedr