WikiDer > Mahsulotning raqamli assortimenti - Vikipediya

Berilgan Hilbert maydoni bilan tensor mahsuloti tuzilish a mahsulotning raqamli diapazoni a deb belgilanadi raqamli diapazon mahsulot vektorlarining pastki qismiga nisbatan. Ba'zi vaziyatlarda, ayniqsa kvant mexanikasi mahsulotning raqamli diapazoni sifatida tanilgan mahalliy raqamlar diapazoni

Kirish

Ruxsat bering ${ displaystyle X}$ an-da ishlaydigan operator bo'ling ${ displaystyle N}$- o'lchovli Hilbert maydoni ${ displaystyle { mathcal {H}} _ {N}}$. Ruxsat bering ${ displaystyle mathrm { Lambda} (X)}$ uni belgilang raqamli diapazon, ya'ni barchasi to'plami ${ displaystyle lambda}$ Shunday qilib, normal holat mavjud ${ displaystyle {| psi rangle} in { mathcal {H}} _ {N}}$, ${ displaystyle || psi || = 1}$, bu qondiradi ${ displaystyle { langle psi |} X {| psi rangle} = lambda}$.

Shunga o'xshash tushunchani tenzor mahsuloti tuzilishi bilan kompozitsion Hilbert fazosida ishlaydigan operatorlar uchun aniqlash mumkin. Avvaliga ikki qismli Hilbert makonini ko'rib chiqing, ${ displaystyle { mathcal {H}} _ {N} = { mathcal {H}} _ {K} otimes { mathcal {H}} _ {M},}$ kompozit o'lchov ${ displaystyle N = KM}$.

Ruxsat bering ${ displaystyle X}$ kompozit Hilbert fazosida ishlaydigan operator bo'ling. Biz belgilaymiz mahsulotning raqamli diapazoni ${ displaystyle mathrm { Lambda} ^ {! otimes} ! chap (X o'ng)}$ ning ${ displaystyle X}$, ning tensor mahsuloti tuzilishiga nisbatan ${ displaystyle { mathcal {H}} _ {N}}$, kabi ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left (X right) = left {{ langle psi _ {A} otimes psi _ {B} |} X {| psi _ {A} otimes psi _ {B} rangle}: {| psi _ {A} rangle} in { mathcal {H}} _ {K}, {| psi _ {B} rangle} in { mathcal {H}} _ {M} right },}$ qayerda ${ displaystyle {| psi _ {A} rangle} in { mathcal {H}} _ {K}}$ va ${ displaystyle {| psi _ {B} rangle} in { mathcal {H}} _ {M}}$ normallashtirilgan.

Mahsulotning raqamli radiusi

Ruxsat bering ${ displaystyle { mathcal {H}} _ {N} = { mathcal {H}} _ {K} otimes { mathcal {H}} _ {M}}$ Tensorli mahsulot Hilbert fazosi bo'ling. Biz belgilaymiz mahsulotning radiusi ${ displaystyle r ^ { otimes} (X)}$ ning ${ displaystyle X}$, bu tensor mahsulotining tuzilishiga nisbatan, kabi ${ displaystyle r ^ { otimes} (X) = max {| z |: z in mathrm { Lambda} ^ {! otimes} ! left (X right) }.}$

Notation

So'nggi bir necha o'n yilliklar davomida ma'lum bir operatorning "qiymatlar maydoni" deb nomlangan raqamli diapazoni tushunchasi keng o'rganilgan va uning kvant nazariyasida foydaliligi ta'kidlangan. Raqamli diapazonning bir nechta umumlashtirilishi ma'lum. Xususan, Markus xususiyatlariga katta qiziqish uyg'otadigan '' 'parchalanadigan sonli diapazon' '' tushunchasini kiritdi.

Mahsulotning raqamli diapazoni tensor mahsuloti Hilbert fazasida ishlaydigan operatorlar uchun belgilangan parchalanadigan sonli diapazonning ma'lum bir holi sifatida qaralishi mumkin. Ushbu tushuncha raqamli diapazon sifatida ham ko'rib chiqilishi mumkin nisbiy tegishli kichik guruhga ${ displaystyle U (K) marta U (M)}$ to'liq unitar guruhning ${ displaystyle U (KM)}$.

Mahsulot raqamli assortimentining xususiyatlari

Ushbu bo'lim bo'sh. Siz yordam berishingiz mumkin unga qo'shilish. (2012 yil aprel)

Umumiy ish

Mahsulotning raqamli diapazonining Hilbert kosmosining bo'linmasidan va operatorning tuzilishidan mustaqil bo'lgan asosiy xususiyatlarini aniqlash qiyin emas. Quyida ularni oddiy narsalarni qoldirib, dalilsiz qoldiramiz.

Asosiy xususiyatlar

Umumiy operatorlar uchun mahsulotning raqamli doirasiga oid topologik faktlar.

1. Mahsulotning raqamli diapazoni murakkab tekislikda bog'langan to'plamni hosil qiladi. Bu to'g'ri, chunki mahsulotning raqamli diapazoni ulangan to'plamning doimiy tasviridir.
2. Mahsulotning raqamli assortimenti subadditive hisoblanadi. Barcha uchun ${ displaystyle A, B in mathbb {M} _ {n}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left (A + B right) subset mathrm { Lambda} ^ {! otimes} ! left (A right ) + mathrm { Lambda} ^ {! otimes} ! chap (B o'ng).}$
3. Barcha uchun ${ displaystyle A in mathbb {M} _ {n}}$ va ${ displaystyle alpha in mathbb {C}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({A + alpha mathbf {I}} right) = mathrm { Lambda} ^ {! otimes} ! chap (A o'ng) + alfa.}$
4. Barcha uchun ${ displaystyle A in mathbb {M} _ {n}}$ va ${ displaystyle alpha in mathbb {C}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({ alfa A} right) = alpha mathrm { Lambda} ^ {! otimes} ! left ( {A} o'ng).}$
5. Barcha uchun ${ displaystyle A in mathbb {M} _ {m times n}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({(U otimes V) A (U otimes V) ^ { xanjar}} right) = mathrm { Lambda } ^ {! otimes} ! chap ({A} o'ng),}$ unitar uchun ${ displaystyle U in mathbb {M} _ {m}}$ va ${ displaystyle V in mathbb {M} _ {n}}$.
6. Ruxsat bering ${ displaystyle A in mathbb {M} _ {m}}$ va ${ displaystyle B in mathbb {M} _ {n}}$

• Agar ulardan biri normal bo'lsa, unda ularning tenzor mahsulotining sonli diapazoni mahsulot sonining konveks tanasiga to'g'ri keladi, ${ displaystyle mathrm { Lambda} (A otimes B) = mathrm {Co} ( mathrm { Lambda} ^ {! otimes} ! left ({A otimes B} right)) .}$
• Agar ${ displaystyle e ^ {i theta} A}$ ba'zilari uchun ijobiy yarim yarim ${ displaystyle theta in [0,2 pi)}$, keyin ${ displaystyle mathrm { Lambda} (A otimes B) = mathrm { Lambda} ^ {! otimes} ! left ({A otimes B} right).}$
• Ruxsat bering ${ displaystyle H (A) = { frac {1} {2}} (A + A ^ { xanjar})}$ va ${ displaystyle S (A) = { frac {1} {2}} (A-A ^ { xanjar})}$.

1. Barcha uchun ${ displaystyle A in mathbb {M} _ {n}}$, bizda ... bor ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({H (A)} right) = mathrm {Re} mathrm { Lambda} ^ {! otimes} ! chap ({A} o'ng)}$ va ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({S (A)} right) = i , mathrm {Im} mathrm { Lambda} ^ {! otimes} ! chap ({A} o'ng).}$

Qavariqlik

Mahsulotning raqamli doirasi konveks bo'lishi shart emas. Quyidagi oddiy misolni ko'rib chiqing. Ruxsat bering

${ displaystyle A = left ({ begin {array} {cc} 1 & 0 0 & 0 end {array}} right) otimes left ({ begin {array} {cc} 1 & 0 0 & 0 end {array}} right) + i chap ({ begin {array} {cc} 0 & 0 0 & 1 end {array}} right) otimes left ({ begin {array} {cc} 0 & 0 ) 0 & 1 end {array}} o'ng).}$

Matritsa ${ displaystyle A}$ Yuqorida tavsiflangan o'z qiymatlari bilan matritsa ${ displaystyle 0,1, i}$. Buni ko'rish oson ${ displaystyle 1 in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$ va ${ displaystyle i in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$, lekin ${ displaystyle (1 + i) / 2 not in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$. Aslida, biz to'g'ridan-to'g'ri hisoblash orqali ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({A} right) = left {x + yi: 0 leq x, 0 leq y, { sqrt { x}} + { sqrt {y}} leq 1 right }.}$

Matritsaning mahsulot sonli diapazoni ${ displaystyle A}$ quyida keltirilgan.

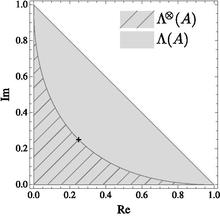
A matritsa uchun raqamli diapazonni (kulrang uchburchak) va mahsulot sonli diapazonni (chiziqli to'plam) taqqoslash.

Mahsulotning raqamli diapazoni umumiy operator uchun bo'sh bo'lmagan to'plamni hosil qiladi. Xususan, u spektrning baritsentrini o'z ichiga oladi.

Bariyenter

Mahsulotning raqamli diapazoni ${ displaystyle A in mathbb {M} _ {K times M}}$ spektrning baritsentrini o'z ichiga oladi, ${ displaystyle { frac {1} {KM}} ; { mathrm {tr}} A in mathrm { Lambda} ^ {! otimes} ! left ({A} right) ).}$

Mahsulotning raqamli radiusi matritsalar bo'yicha vektor normasi, ammo bu matritsa normasi emas. Mahsulotning raqamli radiusi tenzor mahsuloti tarkibiga ega bo'lgan mahalliy birliklarga nisbatan o'zgarmasdir.

Adabiyotlar

• Z. Puchala, P. Gavron, J.A. Misshak, Ł. Skowronek, M.-. Choi, K. Jitskovski, "Tensorli mahsulot tuzilishiga ega bo'lgan bo'shliqdagi mahsulot sonining diapazoni", Lineer Algebra Appl., 434 (2011) 327-342. doi:10.1016 / j.laa.2010.08.026 arXiv:1008.3482.
• P. Gavron, Z. Puchala, J. A. Misshak, Ł. Skovronek, K. Jitskovski, "Cheklangan sonlar diapazoni: kvant ma'lumotlari nazariyasining ko'p qirrali vositasi", J. Matematik. Fizika. 51, 102204 (2010). doi:10.1063/1.3496901 arXiv:0905.3646.