Qadimgi Yunonistonda o'rganilgan klassik o'rtacha ko'rsatkichlar
Kvadratik o'rtacha va Pifagoriya vositalarining (ikki sonli) geometrik qurilishi
a va
b ). Garmonik o'rtacha
H , geometrik tomonidan
G , arifmetikasi
A va kvadratik o'rtacha (shuningdek, sifatida tanilgan
o'rtacha kvadrat ) bilan belgilanadi
Q .
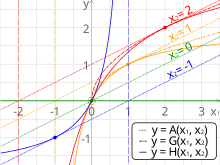
Juft sonlarning arifmetik, geometrik va garmonik vositalarini taqqoslash. Vertikal kesilgan chiziqlar
asimptotlar harmonik vositalar uchun.
Matematikada uchta klassik Pifagor degani ular o'rtacha arifmetik (AM), the o'rtacha geometrik (GM) va garmonik o'rtacha (HM). Bular degani tomonidan mutanosib ravishda o'rganilgan Pifagorchilar va yunon matematiklarining keyingi avlodlari[1]
Ta'rif
Ular quyidagilar bilan belgilanadi:
AM ( x 1 , … , x n ) = 1 n ( x 1 + ⋯ + x n ) GM ( x 1 , … , x n ) = | x 1 × ⋯ × x n | n HM ( x 1 , … , x n ) = n 1 x 1 + ⋯ + 1 x n { displaystyle { begin {aligned} operatorname {AM} left (x_ {1}, ; ldots, ; x_ {n} right) & = { frac {1} {n}} left (x_ {1} + ; cdots ; + x_ {n} o'ng) [9pt] operatorname {GM} left (x_ {1}, ; ldots, ; x_ {n} o'ng) & = { sqrt [{n}] { chap vert x_ {1} times , cdots , times x_ {n} right vert}} [9pt] operatorname {HM } chap (x_ {1}, ; ldots, ; x_ {n} o'ng) & = { frac {n} { displaystyle { frac {1} {x_ {1}}} + ; cdots ; + { frac {1} {x_ {n}}}}} end {aligned}}} Xususiyatlari
Har biri o'rtacha, M { textstyle operator nomi {M}}
Birinchi buyurtma bir xillik M ( b x 1 , … , b x n ) = b M ( x 1 , … , x n ) { displaystyle operator nomi {M} (bx_ {1}, , ldots, , bx_ {n}) = b operator nomi {M} (x_ {1}, , ldots, , x_ {n} )} Almashinuv ostida o'zgaruvchanlik M ( … , x men , … , x j , … ) = M ( … , x j , … , x men , … ) { displaystyle operator nomi {M} ( ldots, , x_ {i}, , ldots, , x_ {j}, , ldots) = = operator nomi {M} ( ldots, , x_ { j}, , ldots, , x_ {i}, , ldots)} har qanday kishi uchun men { displaystyle i} j { displaystyle j} Monoton a < b → M ( a , x 1 , x 2 , … x n ) < M ( b , x 1 , x 2 , … x n ) { displaystyle a Tushkunlik ∀ x , M ( x , x , … x ) = x { displaystyle forall x, ; M (x, x, ldots x) = x} Monotoniklik va idempotensiya shuni anglatadiki, to'plam o'rtacha har doim to'plamning haddan tashqari tomonlari orasida bo'ladi.
min ( x 1 , … , x n ) ≤ M ( x 1 , … , x n ) ≤ maksimal ( x 1 , … , x n ) { displaystyle min (x_ {1}, , ldots, , x_ {n}) leq operator nomi {M} (x_ {1}, , ldots, , x_ {n}) leq max (x_ {1}, , ldots, , x_ {n})} Garmonik va arifmetik vositalar ijobiy dalillar uchun bir-birining o'zaro duallari:
HM ( 1 x 1 , … , 1 x n ) = 1 AM ( x 1 , … , x n ) { displaystyle operator nomi {HM} chap ({ frac {1} {x_ {1}}}, , ldots, , { frac {1} {x_ {n}}} o'ng) = { frac {1} { operator nomi {AM} chap (x_ {1}, , ldots, , x_ {n} o'ng)}}} geometrik o'rtacha esa o'zaro dual:
GM ( 1 x 1 , … , 1 x n ) = 1 GM ( x 1 , … , x n ) { displaystyle operatorname {GM} chap ({ frac {1} {x_ {1}}}, , ldots, , { frac {1} {x_ {n}}} o'ng) = { frac {1} { operatorname {GM} chap (x_ {1}, , ldots, , x_ {n} o'ng)}}} Vositalar orasidagi tengsizlik
Ushbu vositalarga buyurtma mavjud (agar barchasi bo'lsa) x men { displaystyle x_ {i}}
min ≤ HM ≤ GM ≤ AM ≤ maksimal { displaystyle min leq operator nomi {HM} leq operator nomi {GM} leq operator nomi {AM} leq max} tenglikni ushlab turish bilan va agar shunday bo'lsa x men { displaystyle x_ {i}}
Bu .ning umumlashtirilishi arifmetik va geometrik vositalarning tengsizligi va uchun tengsizlikning maxsus holati umumlashtirilgan vositalar . Dalil o'rtacha arifmetik-geometrik tengsizlik , AM ≤ maksimal { displaystyle operator nomi {AM} leq max} min { displaystyle min} maksimal { displaystyle max}
Pifagor vositalarini o'rganish o'rganish bilan chambarchas bog'liq ixtisoslashtirish va Shur-konveks funktsiyalari . Garmonik va geometrik vositalar ularning argumentlarining konkav simmetrik funktsiyalari va shu sababli Shur-konkav, arifmetik o'rtacha esa uning argumentlarining chiziqli funktsiyasi, shuning uchun ham konkav va konveks.
Shuningdek qarang
Adabiyotlar
^ Xit, Tomas. Qadimgi yunon matematikasi tarixi . ^ Agar AC = a va miloddan avvalgi = b . OC = AM ning a va b va radius r = QO = OG.Pifagor teoremasi , QC² = QO² + OC² ∴ QC = √QO² + OC² = QM .OC² - OG² = GM .o'xshash uchburchaklar , HC / GC GC / OC GC² / OC HM . Tashqi havolalar


![{ displaystyle { begin {aligned} operatorname {AM} left (x_ {1}, ; ldots, ; x_ {n} right) & = { frac {1} {n}} left (x_ {1} + ; cdots ; + x_ {n} o'ng) [9pt] operatorname {GM} left (x_ {1}, ; ldots, ; x_ {n} o'ng) & = { sqrt [{n}] { chap vert x_ {1} times , cdots , times x_ {n} right vert}} [9pt] operatorname {HM } chap (x_ {1}, ; ldots, ; x_ {n} o'ng) & = { frac {n} { displaystyle { frac {1} {x_ {1}}} + ; cdots ; + { frac {1} {x_ {n}}}}} end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bbc1d421516030837da58eb09d16d4c9a93a6f3)














