WikiDer > Ikkinchi asosiy shakl

Yilda differentsial geometriya, ikkinchi asosiy shakl (yoki shakl tensori) a kvadratik shakl ustida teginuvchi tekislik a silliq sirt uch o'lchovli Evklid fazosi, odatda tomonidan belgilanadi ${ displaystyle mathrm {I ! I}}$ ("ikkita" ni o'qing). Bilan birga birinchi asosiy shakl, u sirtning tashqi invariantlarini aniqlashga xizmat qiladi, uning asosiy egriliklar. Umuman olganda, bunday kvadrat shakli silliq suvga cho'mish uchun belgilanadi submanifold a Riemann manifoldu.

Rdagi sirt³

Ikkinchi asosiy shaklning ta'rifi

Motivatsiya

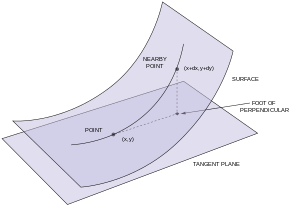
A-ning ikkinchi asosiy shakli parametrli sirt S yilda R³ tomonidan kiritilgan va o'rganilgan Gauss. Birinchidan, sirt ikki baravar grafigi deb taxmin qiling doimiy ravishda farqlanadigan funktsiyasi, z = f(x,y)va bu samolyot z = 0 bu teginish kelib chiqishi yuzasiga. Keyin f va uning qisman hosilalar munosabat bilan x va y (0,0) da yo'qoladi. Shuning uchun Teylorning kengayishi ning f (0,0) da kvadratik atamalar bilan boshlanadi:

${ displaystyle z = L { frac {x ^ {2}} {2}} + Mxy + N { frac {y ^ {2}} {2}} + { text {yuqori buyurtma shartlari}} , ,}$

va koordinatalarda kelib chiqadigan ikkinchi asosiy shakl (x,y) bo'ladi kvadratik shakl

${ displaystyle L , dx ^ {2} + 2M , dx , dy + N , dy ^ {2} ,.}$

Yumshoq nuqta uchun P kuni S, koordinata tizimini shunday koordinatani tanlash mumkin z- samolyot tegib turadi S da P va xuddi shu tarzda ikkinchi asosiy shaklni aniqlang.

Klassik yozuv

Umumiy parametrli sirtning ikkinchi asosiy shakli quyidagicha aniqlanadi. Ruxsat bering r = r(siz,v) yuzasining muntazam parametrlanishi bo'lishi R³, qayerda r silliqdir vektorli funktsiya ikkita o'zgaruvchidan. Ning qisman hosilalarini belgilash odatiy holdir r munosabat bilan siz va v tomonidan r_siz va r_v. Parametrlashning muntazamligi shuni anglatadiki r_siz va r_v har qanday kishi uchun chiziqli ravishda mustaqil (siz,v) domenida rva shu sababli teginuvchi tekislikgacha S har bir nuqtada. Teng ravishda o'zaro faoliyat mahsulot r_siz × r_v sirt uchun normal nolga teng bo'lmagan vektor. Parametrlash, shuning uchun birlik normal vektorlar maydonini belgilaydi n:

${ displaystyle mathbf {n} = { frac { mathbf {r} _ {u} times mathbf {r} _ {v}} {| mathbf {r} _ {u} times mathbf { r} _ {v} |}} ,.}$

Ikkinchi asosiy shakl odatda quyidagicha yoziladi

${ displaystyle mathrm {I ! I} = L , du ^ {2} + 2M , du , dv + N , dv ^ {2} ,,}$

uning matritsasi asosda {r_siz, r_v} teginuvchi tekislikning

${ displaystyle { begin {bmatrix} L&M M&N end {bmatrix}} ,.}$

Koeffitsientlar L, M, N parametrli berilgan nuqtada uv-plane ning ikkinchi qismli hosilalarining proektsiyalari bilan berilgan r shu nuqtada normal chiziqqa S va yordamida hisoblash mumkin nuqta mahsuloti quyidagicha:

${ displaystyle L = mathbf {r} _ {uu} cdot mathbf {n} ,, quad M = mathbf {r} _ {uv} cdot mathbf {n} ,, quad N = mathbf {r} _ {vv} cdot mathbf {n} ,.}$

Uchun imzolangan masofa maydoni ning Gessian H, ikkinchi asosiy shakl koeffitsientlarini quyidagicha hisoblash mumkin:

${ displaystyle L = - mathbf {r} _ {u} cdot mathbf {H} cdot mathbf {r} _ {u} ,, quad M = - mathbf {r} _ {u} cdot mathbf {H} cdot mathbf {r} _ {v} ,, quad N = - mathbf {r} _ {v} cdot mathbf {H} cdot mathbf {r} _ {v} ,.}$

Fizikning yozuvi

Umumiy parametrli sirtning ikkinchi asosiy shakli S quyidagicha ta'riflanadi.

Ruxsat bering r = r(siz¹,siz²) yuzasining muntazam parametrlanishi bo'lishi R³, qayerda r silliqdir vektorli funktsiya ikkita o'zgaruvchidan. Ning qisman hosilalarini belgilash odatiy holdir r munosabat bilan siz^a tomonidan r_a, a = 1, 2. Parametrlashning muntazamligi shuni anglatadiki r₁ va r₂ har qanday kishi uchun chiziqli ravishda mustaqil (siz¹,siz²) domenida rva shu sababli teginuvchi tekislikgacha S har bir nuqtada. Teng ravishda o'zaro faoliyat mahsulot r₁ × r₂ sirt uchun normal nolga teng bo'lmagan vektor. Parametrlash, shuning uchun birlik normal vektorlari maydonini belgilaydi n:

${ displaystyle mathbf {n} = { frac { mathbf {r} _ {1} times mathbf {r} _ {2}} {| mathbf {r} _ {1} times mathbf { r} _ {2} |}} ,.}$

Ikkinchi asosiy shakl odatda quyidagicha yoziladi

${ displaystyle mathrm {I ! I} = b _ { alpha beta} , du ^ { alpha} , du ^ { beta} ,.}$

Yuqoridagi tenglamada Eynshteyn konvensiyasi.

Koeffitsientlar b_aβ parametrli berilgan nuqtada siz¹siz²-plane ning ikkinchi qismli hosilalarining proektsiyalari bilan berilgan r shu nuqtada normal chiziqqa S va normal vektor bo'yicha hisoblash mumkin n quyidagicha:

${ displaystyle b _ { alpha beta} = r _ {, alpha beta} ^ { , gamma} n _ { gamma} ,.}$

Riemann manifoldidagi gipersurfey

Yilda Evklid fazosi, ikkinchi asosiy shakl tomonidan berilgan

${ displaystyle mathrm {I ! I} (v, w) = - langle d nu (v), w rangle nu}$

qayerda ν bo'ladi Gauss xaritasiva dν The differentsial ning ν sifatida qaraladi vektor bilan baholanadigan differentsial shaklva qavslar metrik tensor Evklid fazosining

Umuman olganda, Riemann kollektorida ikkinchi asosiy shakl tasvirlashning ekvivalent usuli hisoblanadi shakl operatori (bilan belgilanadi S) gipersurf,

${ displaystyle mathrm {I} ! mathrm {I} (v, w) = lang S (v), w rangle n = - langle nabla _ {v} n, w rangle n = langle n, nabla _ {v} w rangle n ,,}$

qayerda ∇_vw belgisini bildiradi kovariant hosilasi atrof-muhit manifoldining va n gipersurfdagi normal vektorlar maydoni. (Agar affine ulanish bu burilishsiz, keyin ikkinchi asosiy shakl nosimmetrikdir.)

Ikkinchi asosiy shaklning belgisi yo'nalishni tanlashga bog'liq n (bu yuqori sathning birgalikan yo'nalishi deb ataladi - Evklid fazosidagi sirtlar uchun bu teng ravishda berilgan yo'nalish sirt).

O'zboshimchalik bilan kodlashtirishga umumlashtirish

Ikkinchi asosiy shakl o'zboshimchalik bilan umumlashtirilishi mumkin kod o'lchovi. U holda bu tegins fazadagi kvadratik shakl bo'lib, ichida qiymatlari mavjud oddiy to'plam va u tomonidan belgilanishi mumkin

${ displaystyle mathrm {I ! I} (v, w) = ( nabla _ {v} w) ^ { bot} ,,}$

qayerda (∇_vw)^⊥ ning ortogonal proyeksiyasini bildiradi kovariant hosilasi ∇_vw oddiy to'plamga.

Yilda Evklid fazosi, egrilik tensori a submanifold quyidagi formula bilan tavsiflanishi mumkin:

${ displaystyle langle R (u, v) w, z rangle = langle mathrm {I} ! mathrm {I} (u, z), mathrm {I} ! mathrm {I} ( v, w) rangle - langle mathrm {I} ! mathrm {I} (u, w), mathrm {I} ! mathrm {I} (v, z) rangle.}$

Bunga Gauss tenglamasi, chunki u Gaussning umumlashtirilishi sifatida qaralishi mumkin Egregiya teoremasi.

Umumiy Riemann manifoldlari uchun atrof makonining egriligini qo'shish kerak; agar N ga o'rnatilgan manifold Riemann manifoldu (M,g) keyin egrilik tensori R_N ning N indüklenen metrik bilan ikkinchi asosiy shakl va yordamida ifodalanishi mumkin R_M, egrilik tenzori M:

${ displaystyle langle R_ {N} (u, v) w, z rangle = langle R_ {M} (u, v) w, z rangle + langle mathrm {I} ! mathrm {I } (u, z), mathrm {I} ! mathrm {I} (v, w) rangle - langle mathrm {I} ! mathrm {I} (u, w), mathrm { I} ! Mathrm {I} (v, z) rangle ,.}$

Shuningdek qarang

• Birinchi asosiy shakl
• Gauss egriligi
• Gauss-Kodassi tenglamalari
• Shakl operatori
• Uchinchi asosiy shakl
• Tautologik bir shakl

Adabiyotlar

• Guggenxaymer, Geynrix (1977). "10-bob. Yuzalar". Differentsial geometriya. Dover. ISBN 0-486-63433-7.
• Kobayashi, Shoshichi va Nomizu, Katsumi (1996). Differentsial geometriya asoslari, jild. 2018-04-02 121 2 (Yangi tahr.). Wiley-Intertersience. ISBN 0-471-15732-5.
• Spivak, Maykl (1999). Differentsial geometriyaga keng kirish (3-jild). Nashr qiling yoki halok bo'ling. ISBN 0-914098-72-1.

Tashqi havolalar

• Stiven Verpoort (2008) Ikkinchi asosiy shakldagi geometriya: egrilik xususiyatlari va o'zgaruvchan jihatlar dan Katholieke Universiteit Leuven.