WikiDer > Omon qolish funktsiyasi

Survival function

The omon qolish funktsiyasi a funktsiya bu beradi ehtimollik bemor, qurilma yoki boshqa qiziqish uyg'otadigan narsa omon qolish belgilangan vaqtdan tashqari.^[1]

Tirik qolish funktsiyasi shuningdek omon qolish funktsiyasi^[2] yoki ishonchlilik funktsiyasi.^[3]

Atama ishonchlilik funktsiyasi ichida keng tarqalgan muhandislik muddat esa omon qolish funktsiyasi dasturlarning keng doirasi, shu jumladan inson o'limida qo'llaniladi. Tirik qolish funktsiyasining yana bir nomi bu komplementar kümülatif taqsimlash funktsiyasi.

Ta'rif

Ruxsat bering T bilan uzluksiz tasodifiy o'zgaruvchi bo'ling kümülatif taqsimlash funktsiyasi F(t) [0, ∞) oralig'ida. Uning omon qolish funktsiyasi yoki ishonchlilik funktsiyasi bu:

{ displaystyle S (t) = P ( {T> t }) ​​= int _ {t} ^ { infty} f (u) , du = 1-F (t).}

Tirik qolish funktsiyalariga misollar

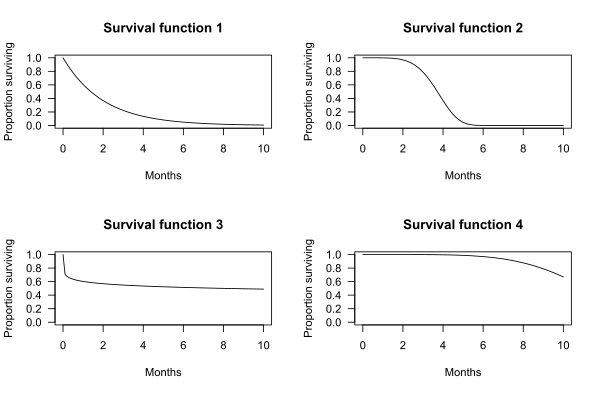
Quyidagi grafikalarda gipotetik omon qolish funktsiyalarining namunalari keltirilgan. X o'qi vaqt. Y o'qi - bu tirik qolganlarning nisbati. Grafiklarda mavzuning t vaqtdan keyin omon qolish ehtimoli ko'rsatilgan.

Masalan, tirik qolish funktsiyasi 1 uchun t = 2 oydan uzoqroq yashash ehtimoli 0,37 ga teng. Ya'ni, sub'ektlarning 37% 2 oydan ko'proq omon qoladi.

Omon qolish funktsiyasi 2 uchun t = 2 oydan uzoqroq yashash ehtimoli 0,97 ga teng. Ya'ni, sub'ektlarning 97% 2 oydan ko'proq omon qoladi.

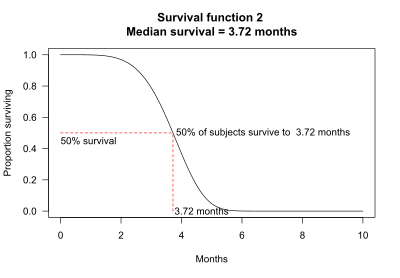
Median omon qolish omon qolish funktsiyasidan aniqlanishi mumkin. Masalan, 2-omon qolish funktsiyasi uchun sub'ektlarning 50% 3.72 oy davomida omon qoladi. O'rtacha omon qolish 3,72 oyni tashkil qiladi.

Ba'zi hollarda o'rtacha hayotni grafikadan aniqlash mumkin emas. Masalan, 4-omon qolish funktsiyasi uchun sub'ektlarning 50% dan ortig'i 10 oylik kuzatuv davridan uzoqroq yashaydi.

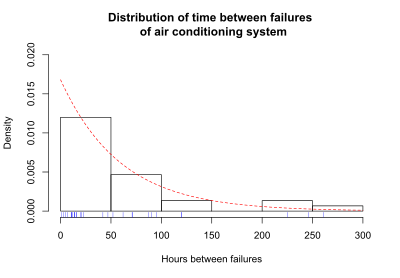
Tirik qolish funktsiyasi - bu tirik qolish ma'lumotlarini tavsiflash va namoyish qilishning bir necha usullaridan biridir. Ma'lumotlarni namoyish qilishning yana bir foydali usuli - bu sub'ektlarning omon qolish vaqtining taqsimlanishini ko'rsatadigan grafik. Olkin,^[4] sahifa 426, tirik qolish ma'lumotlariga quyidagi misol keltiradi. Konditsioner tizimining ketma-ket ishdan chiqishi orasidagi soatlarning soni qayd etildi. Keyingi muvaffaqiyatsizliklar orasidagi vaqt 1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246 va 261 soat. Nosozliklar orasidagi o'rtacha vaqt 59,6 ga teng. Ushbu o'rtacha qiymat ma'lumotlarga nazariy egri chiziqni moslashtirish uchun qisqa vaqt ichida ishlatiladi. Quyidagi rasmda muvaffaqiyatsizliklar orasidagi vaqt taqsimoti ko'rsatilgan. Grafik ostidagi ko'k belgi ketma-ket muvaffaqiyatsizliklar orasidagi haqiqiy soat.

Nosozlik vaqtlarining taqsimlanishi eksponent taqsimotni ifodalovchi egri chiziq bilan ortiqcha yotqizilgan. Ushbu misol uchun eksponensial taqsimot ishdan chiqish vaqtlarining taqsimlanishiga yaqinlashadi. Ko'rsatkichli egri chiziq - bu haqiqiy nosozlik vaqtiga moslashtirilgan nazariy taqsimot. Ushbu o'ziga xos eksponent egri lambda parametri bilan belgilanadi, b = 1 / (xatolar orasidagi o'rtacha vaqt) = 1 / 59.6 = 0.0168. Agar vaqt biron bir ijobiy qiymatni qabul qilishi mumkin bo'lsa, ishlamay qolish vaqtining taqsimlanishi ehtimollik zichligi funktsiyasi (pdf) deb nomlanadi. Tenglamalarda pdf f (t) sifatida ko'rsatilgan. Agar vaqt faqat diskret qiymatlarni qabul qilishi mumkin bo'lsa (masalan, 1 kun, 2 kun va hokazo), ishlamay qolish vaqtining taqsimoti ehtimollik massasi funktsiyasi (pmf). Ko'pgina omon qolish holatlarini tahlil qilish usullari vaqt har qanday ijobiy qiymatga ega bo'lishi mumkin, va f (t) pdf. Agar konditsionerning kuzatilgan nosozliklari orasidagi vaqt ko'rsatkich ko'rsatkichi yordamida taxmin qilinadigan bo'lsa, u holda eksponensial egri chiziq konditsionerning ishlamay qolish vaqtlari uchun f (t) ehtimollik zichligi funktsiyasini beradi.

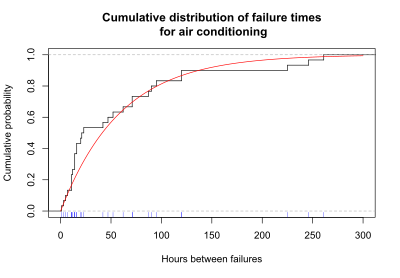
Tirik qolish ma'lumotlarini namoyish qilishning yana bir foydali usuli - bu har bir vaqtgacha bo'lgan yig'ilishlarni aks ettiruvchi grafik. Ushbu ma'lumotlar har safar to'plangan raqam yoki yig'ilish nisbati sifatida ko'rsatilishi mumkin. Quyidagi grafada konditsioner tizim uchun har safar muvaffaqiyatsizliklarning yig'ma ehtimoli (yoki nisbati) ko'rsatilgan. Qora rangdagi zinapoya chizig'i muvaffaqiyatsizliklarning yig'ma nisbatini ko'rsatadi. Har bir qadam uchun grafaning pastki qismida kuzatilgan ishlamay qolish vaqtini ko'rsatadigan ko'k belgi mavjud. Yalang'och qizil chiziq kuzatilgan ma'lumotlarga moslashtirilgan eksponensial egri chiziqni anglatadi.

Har bir nuqtaga qadar muvaffaqiyatsizliklarning yig'ma ehtimoli grafigi kümülatif taqsimlash funktsiyasiyoki CDF. Yashashni tahlil qilishda kümülatif taqsimlash funktsiyasi, tirik qolish vaqtining ma'lum vaqtga, t ga kam yoki teng bo'lish ehtimolini beradi.

T har qanday ijobiy son bo'lgan omon qolish vaqti bo'lsin. Muayyan vaqt kichik t harfi bilan belgilanadi. Ning kümülatif taqsimlash funktsiyasi T funktsiya

{ displaystyle F (t) = operatorname {P} (T leq t),}

bu erda o'ng tomon ehtimollik tasodifiy o'zgaruvchi T dan kam yoki tengdir t. Agar vaqt har qanday ijobiy qiymatni qabul qilishi mumkin bo'lsa, unda F (t) birikma taqsimot funktsiyasi f (t) ehtimollik zichligi funktsiyasining ajralmas qismidir.

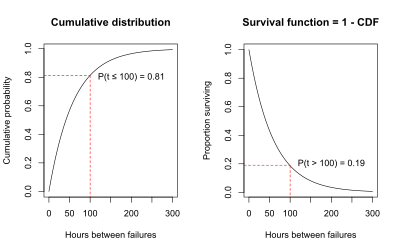
Konditsionerlik namunasi uchun quyida joylashgan CDF grafigi, ishlamay qolish vaqtining 100 soatdan kam yoki teng bo'lish ehtimoli 0,81 ga teng ekanligini ko'rsatadi, bu ma'lumotlarga mos keladigan eksponensial egri chiziq yordamida baholangan.

Nosozlik vaqti ehtimolini grafikalashga alternativa Kamroq 100 soatdan ortiq yoki unga teng bo'lganligi, ishlamay qolish vaqtining ehtimolligini grafika qilishdir kattaroq 100 soatdan ko'proq. Ishdan chiqish vaqtining 100 soatdan katta bo'lish ehtimoli, ishdan chiqish vaqtining 100 soatdan kam yoki unga teng bo'lish ehtimolini olib tashlagan holda 1 bo'lishi kerak, chunki umumiy ehtimollik 1 ga teng bo'lishi kerak.

Bu beradi

P (ishdan chiqish vaqti> 100 soat) = 1 - P (ishlamay qolish vaqti <100 soat) = 1 - 0.81 = 0.19.

Ushbu munosabatlar barcha muvaffaqiyatsizliklar vaqtini umumlashtiradi:

P (T> t) = 1 - P (T

Ushbu munosabatlar quyidagi grafiklarda ko'rsatilgan. Chapdagi grafik P (T t) = 1 - P (T

Parametrik omon qolish funktsiyalari

Ba'zi hollarda, masalan, konditsionerning misoli, omon qolish vaqtining taqsimoti eksponensial taqsimot kabi funktsiya bilan yaqinlashishi mumkin. Odatda omon qolish tahlilida eksponent, Weibull, gamma, normal, log-normal va log-logistic kabi bir nechta tarqatmalar qo'llaniladi.^[3]^[5] Ushbu taqsimotlar parametrlar bilan belgilanadi. Oddiy (Gauss) taqsimoti, masalan, o'rtacha va o'rtacha og'ish parametrlari bilan belgilanadi. Parametrlar bilan aniqlangan omon qolish funktsiyalari parametrik deyiladi.

Yuqorida ko'rsatilgan to'rtta omon qolish funktsiyalari grafikalarida, omon qolish funktsiyasining shakli ma'lum bir ehtimollik taqsimoti bilan belgilanadi: omon qolish funktsiyasi 1 eksponensial taqsimot bilan belgilanadi, 2 Weibull taqsimoti bilan belgilanadi, 3 log-logistik taqsimot bilan belgilanadi , va 4 boshqa Weibull tarqatish bilan belgilanadi.

Eksponensial omon qolish funktsiyasi

Yashashning eksponensial taqsimoti uchun har qanday vaqt oralig'ida, shaxs yoki qurilmaning yoshidan qat'i nazar, muvaffaqiyatsizlik ehtimoli bir xil bo'ladi. Bu haqiqat eksponent saqlanib qolish taqsimotining "xotirasiz" xususiyatiga olib keladi: sub'ektning yoshi keyingi vaqt oralig'ida muvaffaqiyatsizlik ehtimoliga ta'sir qilmaydi. Eksponensial qismlar ishlamay qolganda almashtiriladigan tizim uchun umr bo'yi yaxshi model bo'lishi mumkin.^[6] Shuningdek, u tirik organizmlarning hayotini qisqa vaqt oralig'ida modellashtirish uchun foydali bo'lishi mumkin. Bu tirik organizmning to'liq umr ko'rishining yaxshi modeli bo'lishi ehtimoldan yiroq emas.^[7] Efron va Xasti kabi ^[8](134-bet), "Agar insoniyatning umri eksponensial bo'lsa, unda keksalar yoki yoshlar bo'lmaydi, shunchaki omadli yoki omadsizlar".

Vaybullning omon qolish funktsiyasi

Eksponensial omon qolish funktsiyasining asosiy farazi shundaki, xavf darajasi doimiydir. Yuqorida keltirilgan misolda har yili o'ladigan erkaklar nisbati doimiy ravishda 10% bo'lgan, ya'ni xavf darajasi doimiy bo'lgan. Doimiy xavfni taxmin qilish o'rinli bo'lmasligi mumkin. Masalan, aksariyat tirik organizmlar orasida o'lim xavfi keksa yoshda o'rta yoshdagiga qaraganda ko'proq - ya'ni xavf darajasi vaqt o'tishi bilan ortib boradi. Ba'zi kasalliklar, masalan, ko'krak bezi saratoni uchun 5 yildan keyin takrorlanish xavfi past bo'ladi - ya'ni xavf darajasi vaqt o'tishi bilan kamayadi. The Weibull tarqatish doimiy, ortib boruvchi yoki kamayib boruvchi xavf stavkalarini ta'minlash uchun eksponent taqsimotni kengaytiradi.

Boshqa parametrli omon qolish funktsiyalari

Oddiy, lognormal, log-logistik va gamma kabi ma'lum bir ma'lumotlar to'plamiga yaxshiroq moslashishni ta'minlaydigan bir nechta boshqa parametrli omon qolish funktsiyalari mavjud. Muayyan dastur uchun parametrli taqsimotni tanlash grafik usullar yordamida yoki rasmiy test sinovlari yordamida amalga oshirilishi mumkin, bu taqsimotlar va testlar omon qolish tahlili bo'yicha darsliklarda tasvirlangan.^[1]^[3] Qonunsiz ^[9]parametrli modellarning keng qamroviga ega.

Parametrik omon qolish funktsiyalari odatda ishlab chiqarishda qo'llaniladi, chunki ular kuzatish davridan keyin omon qolish funktsiyasini baholashga imkon beradi. Biroq, parametrli funktsiyalardan to'g'ri foydalanish ma'lumotlarning tanlangan taqsimot bilan yaxshi modellashtirilganligini talab qiladi. Agar tegishli taqsimot mavjud bo'lmasa yoki klinik sinov yoki eksperimentdan oldin aniqlanishi mumkin bo'lmasa, u holda parametrik bo'lmagan omon qolish funktsiyalari foydali alternativani taklif etadi.

Parametrik bo'lmagan omon qolish funktsiyalari

Omon qolishning parametrli modeli mumkin emas yoki kerak emas. Bunday vaziyatlarda omon qolish funktsiyasini modellashtirishning eng keng tarqalgan usuli parametrik emas Kaplan-Meier tahminchisi.

Xususiyatlari

Har qanday omon qolish funktsiyasi S(t) monotonik ravishda kamayadi, ya'ni ${ displaystyle S (u) leq S (t)}$ Barcha uchun ${ displaystyle u> t}$ .

Bu a ning mulkidir tasodifiy o'zgaruvchi odatda o'lim yoki ba'zi bir tizimlarning ishlamay qolishi bilan bog'liq bo'lgan voqealar to'plamini xaritada aks ettiradi vaqt.

The vaqt, t = 0, ba'zi bir kelib chiqishni anglatadi, odatda o'rganish boshlanishi yoki ba'zi bir tizimning ishlashi boshlanadi. S(0) odatda birlikdir, lekin ifodalash uchun kamroq bo'lishi mumkin ehtimollik tizim ishlayotganda darhol ishlamay qolishi.

CDF a bo'lganligi sababli o'ng uzluksiz funktsiya, omon qolish funktsiyasi ${ displaystyle S (t) = 1-F (t)}$ shuningdek, uzluksiz.

Shuningdek qarang

Adabiyotlar

^ ^a ^b Klaynbaum, Devid G.; Klein, Mitchel (2012), Omon qolish tahlili: O'z-o'zidan o'rganiladigan matn (Uchinchi nashr), Springer, ISBN 978-1441966452
^ Stolmen, Mara; Kim, Jong Sung (2003), S yordamida omon qolish tahlili (Birinchi nashr), Chapman va Hall / CRC, ISBN 978-1584884088
^ ^a ^b ^v Ebeling, Charlz (2010), Ishonchlilik va texnik xizmat ko'rsatish muhandisligiga kirish (Ikkinchi nashr), Waveland Press, ISBN 978-1577666257
^ Olkin, Ingram; Gleser, Leon; Derman, Kir (1994), Ehtimollar modellari va ilovalari (Ikkinchi tahr.), Makmillan, ISBN 0-02-389220-X
^ Klayn, Jon; Moeschberger, Melvin (2005), Omon qolish tahlili: Tsenzurali va qisqartirilgan ma'lumotlar uchun usullar (Ikkinchi nashr), Springer, ISBN 978-0387953991
^ Mendenxoll, Uilyam; Terri, Sincich (2007), Muhandislik va fanlarning statistikasi (Beshinchi nashr), Pearson / Prentice Hall, ISBN 978-0131877061
^ Brostrom, Go'ran (2012), R bilan voqea tarixini tahlil qilish (Birinchi nashr), Chapman & Hall / CRC, ISBN 978-1439831649
^ Efron, Bredli; Xasti, Trevor (2016), Kompyuter asri statistik xulosasi: Algoritmlar, dalillar va ma'lumotlar (Birinchi nashr), Kembrij universiteti matbuoti, ISBN 978-1107149892
^ Lawless, Jerald (2002), Hayotiy ma'lumotlarning statistik modellari va usullari (Ikkinchi tahrir), Vili, ISBN 978-0471372158

[KleinbaumKlein2012-1] Klaynbaum, Devid G.; Klein, Mitchel (2012), Omon qolish tahlili: O'z-o'zidan o'rganiladigan matn (Uchinchi nashr), Springer, ISBN 978-1441966452

[TablemanKim2003-2] Stolmen, Mara; Kim, Jong Sung (2003), S yordamida omon qolish tahlili (Birinchi nashr), Chapman va Hall / CRC, ISBN 978-1584884088

[Ebeling2010-3] v Ebeling, Charlz (2010), Ishonchlilik va texnik xizmat ko'rsatish muhandisligiga kirish (Ikkinchi nashr), Waveland Press, ISBN 978-1577666257

[OlkinGleserDerman1994-4] Olkin, Ingram; Gleser, Leon; Derman, Kir (1994), Ehtimollar modellari va ilovalari (Ikkinchi tahr.), Makmillan, ISBN 0-02-389220-X

[Klein2005-5] Klayn, Jon; Moeschberger, Melvin (2005), Omon qolish tahlili: Tsenzurali va qisqartirilgan ma'lumotlar uchun usullar (Ikkinchi nashr), Springer, ISBN 978-0387953991

[Mendenhall2007-6] Mendenxoll, Uilyam; Terri, Sincich (2007), Muhandislik va fanlarning statistikasi (Beshinchi nashr), Pearson / Prentice Hall, ISBN 978-0131877061

[Brostrom2012-7] Brostrom, Go'ran (2012), R bilan voqea tarixini tahlil qilish (Birinchi nashr), Chapman & Hall / CRC, ISBN 978-1439831649

[EfronHastie2016-8] Efron, Bredli; Xasti, Trevor (2016), Kompyuter asri statistik xulosasi: Algoritmlar, dalillar va ma'lumotlar (Birinchi nashr), Kembrij universiteti matbuoti, ISBN 978-1107149892

[Lawless2002-9] Lawless, Jerald (2002), Hayotiy ma'lumotlarning statistik modellari va usullari (Ikkinchi tahrir), Vili, ISBN 978-0471372158

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Navigation