WikiDer > Chorak 5 kubik chuqurchalar

chorak 5 kubik chuqurchalar
(Rasm yo'q)
Turi	Bir xil 5-chuqurchalar
Oila	Chorak giperkubik chuqurchalar
Schläfli belgisi	q {4,3,3,3,4}
Kokseter-Dinkin diagrammasi	=
5 yuz turi	h {4,33}, h4{4,33},
Tepalik shakli	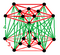Rektifikatsiyalangan 5 hujayrali antiprizm yoki cho'zilgan birlashtirilgan 5-simpleks
Kokseter guruhi	${ displaystyle { tilde {D}} _ {5}}$×2 = [[31,1,3,31,1]]
Ikki tomonlama
Xususiyatlari	vertex-tranzitiv

Yilda besh o'lchovli Evklid geometriyasi, chorak 5 kubik chuqurchalar bir xil bo'shliqni to'ldirishdir tessellation (yoki chuqurchalar). Uning yarim tepaliklari bor 5-demikubik asal, va a tepaliklarining chorak qismi 5 kubik chuqurchasi.^[1] Uning tomonlari 5-demikublar va 5-demikublar.

Bilan bog'liq bo'lgan ko'plab chuqurchalar

Ushbu ko'plab chuqurchalar biridir 20 ta bir xil chuqurchalar tomonidan qurilgan ${ displaystyle { tilde {D}} _ {5}}$ Kokseter guruhi, 3 dan tashqari barchasi boshqa oilalarda kengaytirilgan simmetriya bilan takrorlangan Kokseter-Dinkin diagrammasi. 20 ta almashinish eng yuqori kengaytirilgan simmetriya munosabati bilan keltirilgan:

D5 chuqurchalar
Kengaytirilgan simmetriya	Kengaytirilgan diagramma	Kengaytirilgan guruh	Asal qoliplari
[31,1,3,31,1]		${ displaystyle { tilde {D}} _ {5}}$
<[31,1,3,31,1]> ↔ [31,1,3,3,4]	↔	${ displaystyle { tilde {D}} _ {5}}$×21 = ${ displaystyle { tilde {B}} _ {5}}$	, , , , , ,
[[31,1,3,31,1]]		${ displaystyle { tilde {D}} _ {5}}$×22	,
<2[31,1,3,31,1]> ↔ [4,3,3,3,4]	↔	${ displaystyle { tilde {D}} _ {5}}$×41 = ${ displaystyle { tilde {C}} _ ​​{5}}$	, , , , ,
[<2[31,1,3,31,1]>] ↔ [[4,3,3,3,4]]	↔	${ displaystyle { tilde {D}} _ {5}}$×8 = ${ displaystyle { tilde {C}} _ ​​{5}}$×2	, ,

Shuningdek qarang

5 bo'shliqda muntazam va bir xil chuqurchalar:

• 5 kubik chuqurchasi
• 5-demikub chuqurchasi
• 5-simpleks ko'plab chuqurchalar
• Qisqartirilgan 5-simpleks ko'plab chuqurchalar
• Omnitruncated 5-simplex chuqurchasi

Izohlar

Adabiyotlar

• Kaleydoskoplar: Tanlangan yozuvlari H. S. M. Kokseter, F. Artur Sherk, Piter MakMullen, Entoni C. Tompson, Asia Ivic Weiss, Wiley-Interscience nashri tomonidan tahrirlangan, 1995, ISBN 978-0-471-01003-6 [1]
  • (24-qog'oz) H.S.M. Kokseter, Muntazam va yarim muntazam polipoplar III, [Matematik. Zayt. 200 (1988) 3-45] Qarang: p318 [2]
• Klitzing, Richard. "5D Evklid tesselations # 5D". x3o3o x3o3o * b3 * e - spaquinoh

v t e Asosiy qavariq muntazam va bir xil chuqurchalar 2-9 o'lchovlarda
Bo'shliq	Oila	${ displaystyle { tilde {A}} _ {n-1}}$	${ displaystyle { tilde {C}} _ ​​{n-1}}$	${ displaystyle { tilde {B}} _ {n-1}}$	${ displaystyle { tilde {D}} _ {n-1}}$	${ displaystyle { tilde {G}} _ {2}}$ / ${ displaystyle { tilde {F}} _ {4}}$ / ${ displaystyle { tilde {E}} _ {n-1}}$
E2	Yagona plitka	{3[3]}	δ3	hδ3	qδ3	Olti burchakli
E3	Bir xil konveks chuqurchasi	{3[4]}	δ4	hδ4	qδ4
E4	Bir xil 4-chuqurchalar	{3[5]}	δ5	hδ5	qδ5	24 hujayrali chuqurchalar
E5	Bir xil 5-chuqurchalar	{3[6]}	δ6	hδ6	qδ6
E6	Bir xil 6-chuqurchalar	{3[7]}	δ7	hδ7	qδ7	222
E7	Bir xil 7-chuqurchalar	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Bir xil 8-chuqurchalar	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Bir xil 9-chuqurchalar	{3[10]}	δ10	hδ10	qδ10
En-1	Bir xil (n-1)-chuqurchalar	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21