WikiDer > Shur-Xorn teoremasi

Yilda matematika, ayniqsa chiziqli algebra, Shur-Xorn teoremasinomi bilan nomlangan Issai Shur va Alfred Xorn, a diagonalini xarakterlaydi Ermit matritsasi berilgan bilan o'zgacha qiymatlar. Bu sharoitda tekshiruvlar va jiddiy umumlashmalarga ilhom berdi simpektik geometriya. Bir nechta muhim umumlashmalar Kostantning konveksiya teoremasi, Atiya - Gilyemin - Sternberg konveksiyasi teoremasi, Kirvan konveksiya teoremasi.

Bayonot

Teorema. Ruxsat bering ${ displaystyle mathbf {d} = {d_ {i} } _ {i = 1} ^ {N}}$ va ${ displaystyle mathbf { lambda} = { lambda _ {i} } _ {i = 1} ^ {N}}$ vektorlar bo'lishi ${ displaystyle mathbb {R} ^ {N}}$ shunday qilib, ularning yozuvlari o'sib borayotgan tartibda emas. Bor Ermit matritsasi diagonal qiymatlari bilan ${ displaystyle {d_ {i} } _ {i = 1} ^ {N}}$ va o'ziga xos qiymatlar ${ displaystyle { lambda _ {i} } _ {i = 1} ^ {N}}$ agar va faqat agar

${ displaystyle sum _ {i = 1} ^ {n} d_ {i} leq sum _ {i = 1} ^ {n} lambda _ {i} qquad n = 1,2, ldots, N}$

va

${ displaystyle sum _ {i = 1} ^ {N} d_ {i} = sum _ {i = 1} ^ {N} lambda _ {i}.}$

Polyhedral geometriya istiqboli

Vektor tomonidan yaratilgan permutatsion politop

The permutatsion politop tomonidan yaratilgan ${ displaystyle { tilde {x}} = (x_ {1}, x_ {2}, ldots, x_ {n}) in mathbb {R} ^ {n}}$ bilan belgilanadi ${ displaystyle { mathcal {K}} _ { tilde {x}}}$ to'plamning qavariq tanasi sifatida aniqlanadi ${ displaystyle {(x _ { pi (1)}, x _ { pi (2)}, ldots, x _ { pi (n)}) in mathbb {R} ^ {n}: pi S_ {n} }} da$. Bu yerda ${ displaystyle S_ {n}}$ belgisini bildiradi nosimmetrik guruh kuni ${ displaystyle {1,2, ldots, n }}$. Quyidagi lemma vektorning permutatsion politopini xarakterlaydi ${ displaystyle mathbb {R} ^ {n}}$.

Lemma.^[1][2] Agar ${ displaystyle x_ {1} geq x_ {2} geq cdots geq x_ {n}, y_ {1} geq y_ {2} geq cdots geq y_ {n}}$va ${ displaystyle x_ {1} + x_ {2} + cdots + x_ {n} = y_ {1} + y_ {2} + cdots + y_ {n},}$ keyin quyidagilar teng:

(i) ${ displaystyle (y_ {1}, y_ {2}, cdots, y_ {n}) (= { tilde {y}}) in { mathcal {K}} _ { tilde {x}}}$.

(ii) ${ displaystyle y_ {1} leq x_ {1}, y_ {1} + y_ {2} leq x_ {1} + x_ {2}, ldots, y_ {1} + y_ {2} + cdots + y_ {n-1} leq x_ {1} + x_ {2} + cdots + x_ {n-1}}$

(iii) ball mavjud ${ displaystyle (x_ {1} ^ {(1)}, x_ {2} ^ {(1)}, cdots, x_ {n} ^ {(1)}) (= { tilde {x}} _ {1}), ldots, (x_ {1} ^ {(n)}, x_ {2} ^ {(n)}, ldots, x_ {n} ^ {(n)}) (= { tilde {x}} _ {n})}$ yilda ${ displaystyle { mathcal {K}} _ { tilde {x}}}$ shu kabi ${ displaystyle { tilde {x}} _ {1} = { tilde {x}}, { tilde {x}} _ {n} = { tilde {y}},}$ va ${ displaystyle { tilde {x}} _ {k + 1} = t { tilde {x}} _ {k} + (1-t) tau ({ tilde {x_ {k}}})}}$ har biriga ${ displaystyle k}$ yilda ${ displaystyle {1,2, ldots, n-1 }}$, ba'zi transpozitsiya ${ displaystyle tau}$ yilda ${ displaystyle S_ {n}}$va ba'zilari ${ displaystyle t}$ yilda ${ displaystyle [0,1]}$, bog'liq holda ${ displaystyle k}$.

Shur-Xorn teoremasini isloh qilish

Yuqorida aytib o'tilgan lemmadagi (i) va (ii) ekvivalentligini hisobga olgan holda, teoremani quyidagi tarzda qayta tuzish mumkin.

Teorema. Ruxsat bering ${ displaystyle mathbf {d} = {d_ {i} } _ {i = 1} ^ {N}}$ va ${ displaystyle mathbf { lambda} = { lambda _ {i} } _ {i = 1} ^ {N}}$ haqiqiy vektorlar bo'ling. Bor Ermit matritsasi diagonal yozuvlar bilan ${ displaystyle {d_ {i} } _ {i = 1} ^ {N}}$ va o'ziga xos qiymatlar ${ displaystyle { lambda _ {i} } _ {i = 1} ^ {N}}$ agar va faqat vektor bo'lsa ${ displaystyle (d_ {1}, d_ {2}, ldots, d_ {n})}$ tomonidan yaratilgan permutatsion politopda ${ displaystyle ( lambda _ {1}, lambda _ {2}, ldots, lambda _ {n})}$.

Shuni esda tutingki, ushbu formulada vektorlarning yozuvlariga buyurtma berishga hojat yo'q ${ displaystyle mathbf {d}}$ va ${ displaystyle mathbf { lambda}}$.

Shur-Xorn teoremasining isboti

Ruxsat bering ${ displaystyle A (= a_ {jk})}$ bo'lishi a ${ displaystyle n times n}$ O'ziga xos qiymatlari bo'lgan Hermitian matritsasi ${ displaystyle { lambda _ {i} } _ {i = 1} ^ {n}}$, ko'plik bilan hisoblanadi. Ning diagonalini belgilang ${ displaystyle A}$ tomonidan ${ displaystyle { tilde {a}}}$, vektor sifatida o'ylangan ${ displaystyle mathbb {R} ^ {n}}$va vektor ${ displaystyle ( lambda _ {1}, lambda _ {2}, ldots, lambda _ {n})}$ tomonidan ${ displaystyle { tilde { lambda}}}$. Ruxsat bering ${ displaystyle Lambda}$ ega bo'lgan diagonali matritsa bo'ling ${ displaystyle lambda _ {1}, lambda _ {2}, ldots, lambda _ {n}}$ uning diagonalida.

(${ displaystyle Rightarrow}$) ${ displaystyle A}$ shaklida yozilishi mumkin ${ displaystyle U Lambda U ^ {- 1}}$, qayerda ${ displaystyle U}$ bu unitar matritsa. Keyin

${ displaystyle a_ {ii} = sum _ {j = 1} ^ {n} lambda _ {j} | u_ {ij} | ^ {2}, ; i = 1,2, ldots, n}$

Ruxsat bering ${ displaystyle S = (s_ {ij})}$ tomonidan belgilangan matritsa bo'ling ${ displaystyle s_ {ij} = | u_ {ij} | ^ {2}}$. Beri ${ displaystyle U}$ bu unitar matritsa, ${ displaystyle S}$ a ikki baravar stoxastik matritsa va bizda bor ${ displaystyle { tilde {a}} = S { tilde { lambda}}}$. Tomonidan Birxof-von Neyman teoremasi, ${ displaystyle S}$ permutatsion matritsalarning qavariq birikmasi sifatida yozilishi mumkin. Shunday qilib ${ displaystyle { tilde {a}}}$ tomonidan yaratilgan permutatsion politopda ${ displaystyle { tilde { lambda}}}$. Bu Shur teoremasini isbotlaydi.

(${ displaystyle Leftarrow}$) Agar ${ displaystyle { tilde {a}}}$ xos qiymatlari bilan Ermit matritsasining diagonalida uchraydi ${ displaystyle { lambda _ {i} } _ {i = 1} ^ {n}}$, keyin ${ displaystyle t { tilde {a}} + (1-t) tau ({ tilde {a}})}$ har qanday transpozitsiya uchun bir xil o'ziga xos qiymatlar to'plamiga ega bo'lgan ba'zi bir Ermit matritsasining diagonali sifatida ham uchraydi. ${ displaystyle tau}$ yilda ${ displaystyle S_ {n}}$. Buni quyidagi usulda isbotlash mumkin.

Ruxsat bering ${ displaystyle xi}$ murakkab sonli modul bo'ling ${ displaystyle 1}$ shu kabi ${ displaystyle { overline { xi a_ {jk}}} = - xi a_ {jk}}$ va ${ displaystyle U}$ bilan unitar matritsa bo'ling ${ displaystyle xi { sqrt {t}}, { sqrt {t}}}$ ichida ${ displaystyle j, j}$ va ${ displaystyle k, k}$ yozuvlar, navbati bilan, ${ displaystyle - { sqrt {1-t}}, xi { sqrt {1-t}}}$ da ${ displaystyle j, k}$ va ${ displaystyle k, j}$ yozuvlar, navbati bilan, ${ displaystyle 1}$ dan tashqari barcha diagonal yozuvlarda ${ displaystyle j, j}$ va ${ displaystyle k, k}$va ${ displaystyle 0}$ boshqa barcha yozuvlarda. Keyin ${ displaystyle UAU ^ {- 1}}$bor ${ displaystyle ta_ {jj} + (1-t) a_ {kk}}$ da ${ displaystyle j, j}$ kirish, ${ displaystyle (1-t) a_ {jj} + ta_ {kk}}$ da ${ displaystyle k, k}$ kirish va ${ displaystyle a_ {ll}}$ da ${ displaystyle l, l}$ kirish qaerda ${ displaystyle l neq j, k}$. Ruxsat bering ${ displaystyle tau}$ ning transpozitsiyasi bo'lishi ${ displaystyle {1,2, ldots, n }}$ bu almashadi ${ displaystyle j}$ va ${ displaystyle k}$.

Keyin ning diagonali ${ displaystyle UAU ^ {- 1}}$ bu ${ displaystyle t { tilde {a}} + (1-t) tau ({ tilde {a}})}$.

${ displaystyle Lambda}$ bu o'z qiymatiga ega bo'lgan Ermit matritsasi ${ displaystyle { lambda _ {i} } _ {i = 1} ^ {n}}$. Yuqorida tilga olingan lemmadagi (i) va (iii) ekvivalentligidan foydalanib, permutatsion politopdagi har qanday vektor tomonidan hosil qilinganligini ko'ramiz. ${ displaystyle ( lambda _ {1}, lambda _ {2}, ldots, lambda _ {n})}$, Hermit matritsasining belgilangan o'ziga xos qiymatlari bilan diagonali sifatida sodir bo'ladi. Bu Xorn teoremasini isbotlaydi.

Simpektik geometriya istiqboli

Schur-Horn teoremasini natijasi sifatida qaralishi mumkin Atiya - Gilyemin - Sternberg konveksiyasi teoremasi quyidagi tartibda. Ruxsat bering ${ displaystyle { mathcal {U}} (n)}$ guruhini belgilang ${ displaystyle n times n}$ unitar matritsalar. Uning algebra algebra, bilan belgilanadi ${ displaystyle { mathfrak {u}} (n)}$, to'plamidir qiyshiq-ermitchi matritsalar. Ikkala makonni aniqlash mumkin ${ displaystyle { mathfrak {u}} (n) ^ {*}}$ Ermit matritsalari to'plami bilan ${ displaystyle { mathcal {H}} (n)}$ chiziqli izomorfizm orqali ${ displaystyle Psi: { mathcal {H}} (n) rightarrow { mathfrak {u}} (n) ^ {*}}$ tomonidan belgilanadi ${ displaystyle Psi (A) (B) = mathrm {tr} (iAB)}$ uchun ${ displaystyle A in { mathcal {H}} (n), B in { mathfrak {u}} (n)}$. Unitar guruh ${ displaystyle { mathcal {U}} (n)}$ harakat qiladi ${ displaystyle { mathcal {H}} (n)}$ konjugatsiya orqali va harakat qiladi ${ displaystyle { mathfrak {u}} (n) ^ {*}}$ tomonidan birgalikda harakat. Ushbu harakatlar ostida, ${ displaystyle Psi}$ bu ${ displaystyle { mathcal {U}} (n)}$-har xil xarita, ya'ni har biri uchun ${ displaystyle U in { mathcal {U}} (n)}$ quyidagi diagramma qatnovi,

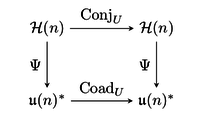
Ruxsat bering ${ displaystyle { tilde { lambda}} = ( lambda _ {1}, lambda _ {2}, ldots, lambda _ {n}) in mathbb {R} ^ {n}}$ va ${ displaystyle Lambda in { mathcal {H}} (n)}$ tomonidan berilgan yozuvlar bilan diagonal matritsani belgilang ${ displaystyle { tilde { lambda}}}$. Ruxsat bering ${ displaystyle { mathcal {O}} _ { tilde { lambda}}}$ orbitasini bildiring ${ displaystyle Lambda}$ ostida ${ displaystyle { mathcal {U}} (n)}$-harakat ya'ni konjugatsiya. Ostida ${ displaystyle { mathcal {U}} (n)}$-ekvariant izomorfizm ${ displaystyle Psi}$, mos keladigan qo'shma orbitadagi simpektik tuzilishga olib kelish mumkin ${ displaystyle { mathcal {O}} _ { tilde { lambda}}}$. Shunday qilib ${ displaystyle { mathcal {O}} _ { tilde { lambda}}}$ Hamiltoniyalik ${ displaystyle { mathcal {U}} (n)}$- ko'p marta.

Ruxsat bering ${ displaystyle mathbb {T}}$ ni belgilang Cartan kichik guruhi ning ${ displaystyle { mathcal {U}} (n)}$ bu modulning diagonal yozuvlari bilan diagonali murakkab matritsalardan iborat ${ displaystyle 1}$. Yolg'on algebra ${ displaystyle { mathfrak {t}}}$ ning ${ displaystyle mathbb {T}}$ diagonal qiyshiq-Ermit matritsalari va ikki fazodan iborat ${ displaystyle { mathfrak {t}} ^ {*}}$ izomorfizm ostida diagonal Ermit matritsalaridan iborat ${ displaystyle Psi}$. Boshqa so'zlar bilan aytganda, ${ displaystyle { mathfrak {t}}}$ faqat xayoliy yozuvlar bilan diagonal matritsalardan iborat va ${ displaystyle { mathfrak {t}} ^ {*}}$ haqiqiy yozuvlari bo'lgan diagonali matritsalardan iborat. Kiritish xaritasi ${ displaystyle { mathfrak {t}} hookrightarrow { mathfrak {u}} (n)}$ xaritani chiqaradi ${ displaystyle Phi: { mathcal {H}} (n) cong { mathfrak {u}} (n) ^ {*} rightarrow { mathfrak {t}} ^ {*}}$, bu matritsani loyihalashtiradi ${ displaystyle A}$ kabi diagonali yozuvlar bilan diagonali matritsaga ${ displaystyle A}$. To'plam ${ displaystyle { mathcal {O}} _ { tilde { lambda}}}$ Hamiltoniyalik ${ displaystyle mathbb {T}}$- ko'p qirrali va cheklash ${ displaystyle Phi}$ ushbu to'plamga a moment xaritasi ushbu harakat uchun.

Atiya-Guillemin-Sternberg teoremasi bo'yicha, ${ displaystyle Phi ({ mathcal {O}} _ { tilde { lambda}})}$ qavariq politopdir. Matritsa ${ displaystyle A in { mathcal {H}} (n)}$ ning har bir elementi konjugatsiya ostida o'rnatiladi ${ displaystyle mathbb {T}}$ agar va faqat agar ${ displaystyle A}$ diagonali. Faqatgina diagonali matritsalar ${ displaystyle { mathcal {O}} _ { tilde { lambda}}}$ diagonal yozuvlari bo'lganlar ${ displaystyle lambda _ {1}, lambda _ {2}, ldots, lambda _ {n}}$ qandaydir tartibda. Shunday qilib, ushbu matritsalar qavariq politopni hosil qiladi ${ displaystyle Phi ({ mathcal {O}} _ { tilde { lambda}})}$. Bu aynan Shur-Xorn teoremasining bayonidir.

Izohlar

Adabiyotlar

• Schur, Issai, Uber eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie, Sitzungsber. Berl. Matematika. Ges. 22 (1923), 9-20.
• Shox, Alfred, Ikki marta stoxastik matritsalar va aylanish matritsasining diagonali, American Journal of Mathematics 76 (1954), 620-630.
• Kadison, R. V.; Pedersen, G. K., Unitar operatorlarning vositalari va konveks kombinatsiyalari, Matematik. Skandal. 57 (1985), 249-266.
• Kadison, R. V., Pifagor teoremasi: I. Cheklangan holat, Proc. Natl. Akad. Ilmiy ish. AQSh, vol. 99 yo'q. 7 (2002): 4178–4184 (elektron)

Tashqi havolalar

• MathWorld
• Terri Tao: 254A, 3a izohlar: Hermit matritsalarining o'ziga xos qiymatlari va yig'indilari
• Sheela Devadas, Piter J. Xeyn, Kiton Stubis: Shur-Xorn teoremasi