WikiDer > Furye konvertatsiyasi
Yilda matematika, a Furye konvertatsiyasi (FT) a matematik o'zgarish parchalanadigan a funktsiya (ko'pincha a vaqtning funktsiyasiyoki a signal) uning tarkibiga kiradi chastotalar, masalan, musiqiy asarni ifodalash akkord uning tarkibiy notalari hajmi va chastotalari bo'yicha. Atama Furye konvertatsiyasi ikkalasiga ham tegishli chastota domeni vakillik va matematik operatsiya chastota domenini vakolatini vaqt funktsiyasi bilan bog'laydigan.
Vaqt funktsiyasining Furye konvertatsiyasi a murakkab qiymatli funktsiya kattaligi (mutlaq qiymat) asl funktsiyasida mavjud bo'lgan va shu kimning chastotasi miqdorini ifodalaydi dalil bo'ladi fazani almashtirish asosiy sinusoid shu chastotada. Furye konvertatsiyasi vaqt funktsiyalari bilan cheklanib qolmaydi, lekin domen asl funktsiyani odatda vaqt domeni. Bundan tashqari teskari Furye konvertatsiyasi tomonidan tasdiqlanganidek, asl funktsiyani chastota domenidan matematik tarzda sintez qiladi Furye inversiya teoremasi.
A sinusoidal egri chiziq, eng yuqori amplituda (1), tepadan tepaga (2), RMS (3) va to'lqin davri (4).
Bitta domenda (vaqt yoki chastota) bajarilgan chiziqli operatsiyalar boshqa sohada tegishli operatsiyalarga ega, ba'zida ularni bajarish osonroq bo'ladi. Ning ishlashi farqlash vaqt domenida chastotani ko'paytirishga to'g'ri keladi,[1-izoh] shuning uchun ba'zi differentsial tenglamalar chastota domenida tahlil qilish osonroq. Shuningdek, konversiya vaqt domenida chastota domenidagi oddiy ko'payishga to'g'ri keladi (qarang Konvolyutsiya teoremasi). Kerakli operatsiyalarni bajargandan so'ng, natijani vaqt sohasiga qaytarish mumkin. Harmonik tahlil chastota va vaqt sohalari o'rtasidagi munosabatlarni, shu jumladan u yoki bu "sodda" funktsiyalar yoki operatsiyalar turlarini o'z ichiga olgan va zamonaviy matematikaning ko'plab sohalari bilan chuqur aloqalarni muntazam ravishda o'rganishdir.
Vaqt domenida joylashgan funktsiyalar chastotalar domeni bo'ylab tarqaladigan Fourier transformatsiyasiga ega va aksincha, bu hodisa noaniqlik printsipi. The tanqidiy bu printsip uchun holat Gauss funktsiyasi, juda muhim ahamiyatga ega ehtimollik nazariyasi va statistika shuningdek, jismoniy hodisalarni namoyish etishda o'rganishda normal taqsimot (masalan, diffuziya). Gauss funktsiyasining Furye konvertatsiyasi yana bir Gauss funktsiyasidir. Jozef Furye o'zgarishini uning ishida joriy qildi issiqlik uzatish, bu erda Gauss funktsiyalari issiqlik tenglamasi.
Furye konvertatsiyasini rasmiy ravishda an deb belgilash mumkin noto'g'ri Riemann integrali, buni qilish integral transformatsiya, garchi ushbu ta'rif yanada murakkab integratsiya nazariyasini talab qiladigan ko'plab dasturlarga mos kelmasa ham.[2-izoh] Masalan, nisbatan ko'p oddiy dasturlarda Dirac delta funktsiyasi, bu rasmiy ravishda xuddi funktsiya kabi muomala qilishi mumkin, ammo asoslash uchun matematik jihatdan yanada murakkab nuqtai nazar kerak.[3-eslatma] Furye konvertatsiyasi, shuningdek, funktsiyasini yuborib, Evklid fazosidagi bir nechta o'zgaruvchilar funktsiyalariga umumlashtirilishi mumkin 3 o'lchovli funktsiyasiga 'joy oralig'i' 3 o'lchovli impuls (yoki bo'shliq va vaqt funktsiyasi funktsiyasiga 4 momentum). Ushbu g'oya fazoviy Fyureni to'lqinlarni o'rganishda ham tabiiy ravishda o'zgartiradi kvant mexanikasi, bu erda to'lqinli echimlarni pozitsiya yoki impulsning funktsiyalari va ba'zan ikkalasining funktsiyalari sifatida namoyish etish muhimdir. Umuman olganda, Furye usullari qo'llaniladigan funktsiyalar murakkab baholanadi va ehtimol vektorli.[4-eslatma] Funktsiyalarni yanada umumlashtirish mumkin guruhlar, bu asl Fourier-dan tashqari ℝ yoki ℝn (qo'shimcha ostida guruh sifatida qaraladi), xususan quyidagilarni o'z ichiga oladi diskret vaqtdagi Furye konvertatsiyasi (DTFT, guruh = ℤ), the diskret Furye konvertatsiyasi (DFT, guruh = ℤ mod N) va Fourier seriyasi yoki dumaloq Furye konvertatsiyasi (guruh = S1, birlik doira end so'nggi nuqtalar aniqlangan yopiq cheklangan interval). Ikkinchisi muntazam ravishda ishlaydi davriy funktsiyalar. The tez Fourier konvertatsiyasi (FFT) - bu DFTni hisoblash algoritmi.
Ta'rif
Funktsiyaning Fourier konvertatsiyasi f an'anaviy ravishda belgilanadi , qo'shib sirkumfleks funktsiya belgisiga. Bir nechtasi bor umumiy konvensiyalar ning Fourier konvertatsiyasini aniqlash uchun integral funktsiya .[1][2] Ulardan biri
| (Tenglama 1) |
har qanday kishi uchun haqiqiy raqam ξ.
Ko'rsatkichdagi manfiy belgining sababi uning ichida keng tarqalganligidir elektrotexnika ga vakillik qilishtomonidan nol boshlang'ich faza va chastotali signal [3][5-eslatma] Salbiy belgi konvensiyasi mahsulotni keltirib chiqaradi qachon 1 (chastota nol) bo'ladi ajralmaslikka olib keladi. Natijada a Dirac delta funktsiyasi da , ning yagona chastota komponenti bo'lgan sinusoidal signal
Qachon mustaqil o'zgaruvchi x ifodalaydi vaqt, o'zgaruvchan o'zgaruvchi ξ ifodalaydi chastota (masalan, vaqt soniya bilan o'lchanadigan bo'lsa, u holda chastota gerts). Muvofiq sharoitlarda, f tomonidan belgilanadi teskari konvertatsiya orqali:
| (Ikkinchi tenglama) |
har qanday haqiqiy raqam uchunx.
Bu bayonot f dan qayta tiklanishi mumkin nomi bilan tanilgan Furye inversiya teoremasiva birinchi marta kiritilgan Furye Issiqlikning analitik nazariyasi,[4][5] zamonaviy me'yorlar bo'yicha dalil deb hisoblanadigan narsa juda kechgacha berilmagan.[6][7] Vazifalar f va ko'pincha a deb nomlanadi Fourier integral juftligi yoki Fourier transform juftligi.[8]
Boshqa umumiy konvensiyalar va ko'rsatmalar uchun, shu jumladan burchak chastotasi ω o'rniga chastota ξ, qarang Boshqa anjumanlar va Boshqa yozuvlar quyida. The Evklid fazosidagi Fourier konvertatsiyasi o'zgaruvchiga ega bo'lgan alohida muomala qilinadi x ko'pincha pozitsiyani va ifodalaydi ξ impuls. Ushbu maqolada tanlangan anjumanlar quyidagilardan iborat harmonik tahlilva Furye konvertatsiyasi ikkalasi bo'ladigan noyob konvensiyalar sifatida tavsiflanadi unitar kuni L2 va algebra homomorfizmi L1 ga L∞, Lebesgue o'lchovini normalizatsiya qilmasdan.[9]
Furye konvertatsiyasining boshqa ko'plab xarakteristikalari mavjud. Masalan, Stoun-fon Neyman teoremasi: Furye konvertatsiyasi noyob yagona intertwiner ning simpektik va Evklid Shredinger vakolatxonalari uchun Heisenberg guruhi.
Tarix
1822 yilda, Jozef Furye ba'zi funktsiyalarni harmonikaning cheksiz yig'indisi sifatida yozish mumkinligini ko'rsatdi.[10]
Kirish

Furye konvertatsiyasining bir turtki o'rganish natijasida kelib chiqadi Fourier seriyasi. Furye qatorlarini o'rganishda murakkab, ammo davriy funktsiyalar matematik tarzda ifodalangan oddiy to'lqinlar yig'indisi sifatida yoziladi sinuslar va kosinuslar. Furye konvertatsiyasi - bu Furye qatorining kengaytmasi bo'lib, u ifodalangan funktsiya davri uzaytirilganda va unga yaqinlashishga ruxsat beriladi. cheksizlik.[11]
Sinus va kosinusning xossalari tufayli har bir to'lqin amplitudasini integral yordamida Furye seriyasida tiklash mumkin. Ko'pgina hollarda foydalanish maqsadga muvofiqdir Eyler formulasi, deb ta'kidlaydi e2πiθ = cos (2πθ) + men gunoh (2πθ), Fourier seriyasini asosiy to'lqinlar bo'yicha yozish e2πiθ. Bu ko'plab formulalarni soddalashtirishning afzalliklariga ega va Fourier seriyasining ushbu maqolada keltirilgan ta'rifga ko'proq o'xshash formulasini taqdim etadi. Sinuslar va kosinuslarni qayta yozish murakkab eksponentlar Furye koeffitsientlarini kompleks baholashni talab qiladi. Ushbu murakkab sonning odatiy talqini shundaki, u ikkalasini ham beradi amplituda funktsiyasida mavjud bo'lgan to'lqinning (yoki kattaligi) va bosqich (yoki dastlabki burchak) to'lqin. Ushbu murakkab eksponentlar ba'zida salbiy "chastotalarni" o'z ichiga oladi. Agar θ soniyalarda, so'ngra to'lqinlarda o'lchanadi e2πiθ va e−2πiθ ikkalasi ham sekundiga bitta tsiklni tugatadi, ammo ular Furye konvertatsiyasidagi turli chastotalarni aks ettiradi. Demak, chastota endi birlik vaqtidagi tsikllar sonini o'lchamaydi, lekin baribir chambarchas bog'liqdir.
Furye seriyasining ta'rifi va funktsiyalar uchun Furye konvertatsiyasi o'rtasida yaqin bog'liqlik mavjud f intervaldan tashqarida nolga teng. Bunday funktsiya uchun biz uning Fourier seriyasini qaerdagi nuqtalarni o'z ichiga olgan har qanday oraliqda hisoblashimiz mumkin f bir xil nolga teng emas. Bunday funktsiya uchun Fourier konvertatsiyasi ham aniqlangan. Furye qatorini hisoblagan interval uzunligini oshirsak, u holda Furye seriyali koeffitsientlari Furye konvertatsiyasiga va Fourier seriyasining yig'indisiga o'xshay boshlaydi. f teskari Furye transformatsiyasiga o'xshay boshlaydi. Aniqroq aytaylik T intervalgacha etarlicha katta [−T/2, T/2] qaysi intervalni o'z ichiga oladi f bir xil nolga teng emas. Keyin nketma-ketlik koeffitsienti vn tomonidan berilgan:
Buni Furye konvertatsiyasining ta'rifi bilan taqqoslaganda, quyidagilar kelib chiqadi:
beri f (x) tashqarida nolga teng [−T/2, T/2]. Shunday qilib, Furye koeffitsientlari kenglik panjarasida namuna olingan Furye konvertatsiyasining qiymatlariga teng 1/T, panjara kengligi bilan ko'paytiriladi 1/T.
Tegishli sharoitlarda, Fourier seriyali f funktsiyaga teng bo'ladi f. Boshqa so'zlar bilan aytganda, f yozilishi mumkin:
bu erda oxirgi yig'indisi ta'riflar yordamida qayta yozilgan birinchi summa ξn = n/Tva Δξ = n + 1/T − n/T = 1/T.
Ushbu ikkinchi sum a Riman summasi. Ruxsat berish orqali T → ∞ u yuqoridagi kabi teskari Furye konvertatsiyasi uchun integralga yaqinlashadi. Tegishli sharoitlarda ushbu dalil aniq bo'lishi mumkin.[12]
Furye qatorlarini o'rganishda raqamlar vn ning Fourier seriyasida mavjud bo'lgan to'lqinning "miqdori" deb o'ylash mumkin edi f. Xuddi shunday, yuqorida ko'rib o'tilganidek, Furye konvertatsiyasi bizning funktsiyamizda har bir individual chastotaning qancha miqdorini o'lchaydigan funktsiya deb qaralishi mumkin. f, va biz asl funktsiyani ko'paytirish uchun integral (yoki "uzluksiz yig'indisi") yordamida bu to'lqinlarni birlashtira olamiz.
Misol
Quyidagi rasmlarda Fourier konvertatsiya qilishning muayyan funktsiyada chastota mavjudligini qanday o'lchashini ingl. Tasvirlangan funktsiya f (t) = cos (6πt) e−πt2 3 da tebranadiHz (agar t soniyani o'lchaydi) va tezda 0 ga intiladi (bu tenglamadagi ikkinchi omil an konvert funktsiyasi uzluksiz sinusoidni qisqa pulsga aylantiradi. Uning umumiy shakli a Gauss funktsiyasi). Ushbu funktsiya osongina chizilgan bo'lishi mumkin bo'lgan haqiqiy Furye konvertatsiyasiga ega bo'lish uchun maxsus tanlangan. Birinchi rasmda uning grafigi mavjud. Hisoblash uchun biz birlashishimiz kerak e−2πmen(3t)f (t). Ikkinchi rasmda ushbu funktsiyaning haqiqiy va xayoliy qismlari syujeti ko'rsatilgan. Integandning haqiqiy qismi deyarli har doim ijobiy bo'ladi, chunki qachon f (t) manfiy, haqiqiy qismi e−2πmen(3t) salbiy ham. Chunki ular qachon, qachon bir xil tezlikda tebranadi f (t) ijobiy, shuning uchun ham haqiqiy qismi e−2πmen(3t). Natijada, integralning haqiqiy qismini birlashtirganda siz nisbatan katta songa ega bo'lasiz (bu holda) 1/2). Boshqa tomondan, mavjud bo'lmagan chastotani o'lchashga urinayotganda, biz ko'rib turganimizdek , siz ushbu funktsiyaning haqiqiy va xayoliy tarkibiy qismlarining uchinchi rasmda tasvirlangan ijobiy va salbiy qiymatlari o'rtasida tez o'zgarib turishini ko'rasiz. Shuning uchun, bu holda integral juda tez tebranadi, shunda integral juda kichik bo'ladi va shu chastota uchun Fyurey konvertatsiyasi qiymati deyarli nolga teng bo'ladi.
Umumiy vaziyat bunga qaraganda biroz murakkabroq bo'lishi mumkin, ammo bu Furye konvertatsiyasi funktsiyada individual chastotaning qancha bo'lishini o'lchash ma'nosida. f (t).
Furye konvertatsiyasining xususiyatlari
Bu erda biz taxmin qilamiz f (x), g(x) va h(x) bor integral funktsiyalar: Lebesgni o'lchash mumkin qoniqarli haqiqiy chiziqda:
Ushbu funktsiyalarning Furye o'zgarishini quyidagicha belgilaymiz f̂ (ξ), ĝ(ξ) va ĥ(ξ) navbati bilan.
Asosiy xususiyatlar
Furye konvertatsiyasi quyidagi asosiy xususiyatlarga ega:[13]
Lineerlik
- Har qanday kishi uchun murakkab sonlar a va b, agar h(x) = af (x) + bg(x), keyin ĥ(ξ) = a · f̂ (ξ) + b · ĝ(ξ).
Tarjima / vaqtni almashtirish

- Har qanday kishi uchun haqiqiy raqam x0, agar h(x) = f (x − x0), keyin ĥ(ξ) = e−2πix0ξ f̂ (ξ).
Modulyatsiya / chastotani almashtirish
- Har qanday kishi uchun haqiqiy raqam ξ0, agar h(x) = e2πixξ0 f (x), keyin ĥ(ξ) = f̂ (ξ − ξ0).
Vaqtni o'lchash
- Nolga teng bo'lmagan uchun haqiqiy raqam a, agar h(x) = f (bolta), keyin
- Ish a = −1 ga olib keladi vaqtni qaytarish mulk, unda quyidagilar ko'rsatilgan: agar h(x) = f (−x), keyin ĥ(ξ) = f̂ (−ξ).
Konjugatsiya
- Agar h(x) = f (x), keyin
- Xususan, agar f haqiqiy bo'lsa, unda bitta haqiqat holati
- anavi, f̂ a Ermit vazifasi. Va agar f sof xayoliy
Vaqtdagi haqiqiy va xayoliy qism
- Agar , keyin .
- Agar , keyin .
Integratsiya
- O'zgartirish ξ = 0 ta'rifda biz olamiz
- Ya'ni, Furye konvertatsiyasini kelib chiqishi bo'yicha baholash (ξ = 0) ning integraliga teng f uning barcha domeni orqali.
Qaytaruvchanlik va davriylik
Funktsiya bo'yicha mos sharoitlarda f, uni Fourier konvertatsiyasidan tiklash mumkin . Darhaqiqat, Furye transformator operatorini F, shuning uchun F( f ) := f̂, keyin mos funktsiyalar uchun Fourier konvertatsiyasini ikki marta qo'llash funktsiyani aylantiradi: F2( f )(x) = f (−x), bu "vaqtni orqaga qaytarish" deb talqin qilinishi mumkin. Vaqtni orqaga qaytarish ikki davriy bo'lgani uchun, buni ikki marta qo'llash hosil beradi F4( f ) = f, shuning uchun Fourier transformatori to'rt davriydir va shunga o'xshash teskari Fourier transformatsiyasini Fourier transformatsiyasini uch marta qo'llash orqali olish mumkin: F3( f̂ ) = f. Xususan, Furye konvertatsiyasi o'zgaruvchan (mos sharoitlarda).
Aniqrog'i, paritet operatori P vaqtni teskari yo'naltiradi, P[ f ] : t ↦ f (−t):
Operatorlarning bu tengliklari, ko'rib chiqilayotgan funktsiyalar maydonini aniq belgilashni, funktsiyalar tengligini belgilashni talab qiladi (har bir nuqtadagi tenglik? Tenglik deyarli hamma joyda?) va operatorlarning tengligini aniqlash - ya'ni ko'rib chiqilayotgan funktsiya maydoni va operatorlar maydoni bo'yicha topologiyani aniqlash. Bular barcha funktsiyalar uchun to'g'ri emas, lekin har xil shakllarning mazmuni bo'lgan har xil sharoitlarda to'g'ri keladi Furye inversiya teoremasi.
Furye konvertatsiyasining bu to'rt karra davriyligi tekislikning 90 ° ga aylanishiga o'xshaydi, ayniqsa, ikki marta takrorlash orqaga qaytishni keltirib chiqaradi va aslida bu o'xshashlikni aniq qilish mumkin. Fourier konvertatsiyasi oddiygina vaqt domenini va chastota domenini almashtirish deb talqin qilinishi mumkin bo'lsa, teskari Fourier konvertatsiyasi ularni orqaga burish bilan, geometrik jihatdan uni 90 ° ga aylanish deb talqin qilish mumkin vaqt chastotasi domeni (vaqtni x-aksis va chastota y-axis), va Furye konvertatsiyasini ga umumlashtirish mumkin kasrli Furye konvertatsiyasi, bu boshqa burchaklar bo'yicha aylanishlarni o'z ichiga oladi. Buni yanada umumlashtirish mumkin chiziqli kanonik o'zgarishlar, ning harakati sifatida tasavvur qilish mumkin maxsus chiziqli guruh SL2(ℝ) ga mos keladigan saqlanib qolgan simpektik shaklga ega bo'lgan vaqt-chastota tekisligida noaniqlik printsipi, quyida. Ushbu yondashuv ayniqsa o'rganilgan signallarni qayta ishlash, ostida vaqt-chastota tahlili.
Birlik va ikkilik
Matematikada ko'pincha biron bir birlikni ikkita o'zgaruvchiga biriktirilgan deb o'ylamaydilar t va ξ. Ammo jismoniy dasturlarda, ξ birliklariga teskari birliklarga ega bo'lishi kerak t. Masalan, agar t soniyalar bilan o'lchanadi, ξformulalar haqiqiy bo'lishi uchun sekundiga tsikllarda bo'lishi kerak. Agar miqyosi t o'zgartirildi va t 2 birliklari bilan o'lchanadiπ soniya, keyin ham ξ "deb nomlangan joyda bo'lishi kerakburchak chastotasi", yoki ba'zi bir formulalarga doimiy koeffitsientni kiritish kerak. Agar t uzunlik birligi bilan o'lchanadi, keyin ξ teskari uzunlikda bo'lishi kerak, masalan, gullar. Ya'ni, haqiqiy chiziqning ikkita nusxasi mavjud: bitta birlik to'plamida o'lchangan, qaerda t intervalgacha, ikkinchisi esa teskari birliklarga tva bu oraliq ξ. Shunday qilib, bu haqiqiy chiziqning ikkita alohida nusxasi va ularni bir-biri bilan aniqlash mumkin emas. Shuning uchun Furye konvertatsiyasi funktsiyalarning bir fazosidan boshqa funktsiyalar makoniga o'tadi: boshqa aniqlanish sohasiga ega funktsiyalar.
Umuman, ξ har doim a bo'lishi kerak chiziqli shakl makonida ts, ya'ni ikkinchi haqiqiy chiziq bu er-xotin bo'shliq birinchi haqiqiy chiziq. Maqolaga qarang chiziqli algebra rasmiyroq tushuntirish va tafsilotlar uchun. Ushbu nuqtai nazar Fyureni umumiyga aylantirishni umumlashtirishda muhim ahamiyat kasb etadi simmetriya guruhlari, shu jumladan Furye seriyasining ishi.
Furye konvertatsiyasida ishtirok etgan haqiqiy chiziqning ikki nusxasini taqqoslash uchun hech kimga ma'qul usul yo'qligi (ko'pincha, "kanonik yo'l yo'q" deyish mumkin) - birliklarni bitta chiziqqa mahkamlash birliklar miqyosini majbur qilmaydi boshqa satr - Furye konvertatsiyasini aniqlash bo'yicha raqib konventsiyalarining ko'pligi uchun sababdir. Turli xil birliklarni tanlash natijasida kelib chiqadigan turli xil ta'riflar har xil konstantalar bilan farq qiladi. Agar birliklari t soniyalarda, lekin birliklari ξ burchak chastotasida, keyin burchak chastotasi o'zgaruvchisi ko'pincha bir yoki boshqa yunoncha harf bilan belgilanadi, masalan, ω = 2πξ juda keng tarqalgan. Shunday qilib (yozuv x̂1 muqobil ta'rifi uchun va x̂ ushbu maqolada qabul qilingan ta'rif uchun)
avvalgidek, ammo keyinchalik tegishli alternativ inversiya formulasi bo'lishi kerak edi
Burchak chastotasini o'z ichiga olgan narsaga ega bo'lish uchun, lekin Furye konvertatsiyasi va inversiya formulasi o'rtasida katta simmetriya bilan, ko'pincha Furye konvertatsiyasining yana bir muqobil ta'rifini koeffitsient bilan ko'rib chiqamiz. √2π, shunday qilib
va mos keladigan inversiya formulasi keyin bo'lishi kerak
FourierTransform buyrug'i tomonidan ishlatiladigan ba'zi bir noodatiy konventsiyalarda Wolfram tili, Fourier konvertatsiyasi mavjud men o'rniga eksponentda −men, va aksincha teskari formulada. Furye konvertatsiyasiga taalluqli ko'pgina identifikatorlar ushbu konventsiyalarda, agar aniq o'z ichiga olgan barcha shartlar mavjud bo'lsa, amal qiladi men uning o'rnini egallash −men.
Masalan, ehtimollar nazariyasida xarakterli funktsiya ϕ ehtimollik zichligi funktsiyasining f tasodifiy o'zgaruvchining X doimiy tip eksponentda salbiy belgisiz va ning birliklaridan aniqlanadi x e'tiborga olinmaydi, 2 yo'qπ yoki:
(Ehtimollar nazariyasida va matematik statistikada Furye - Stieltjes konvertatsiyasidan foydalanish afzalroq, chunki juda ko'p tasodifiy o'zgaruvchilar doimiy tipda emas va zichlik funktsiyasiga ega emas va funktsiyalarga emas, balki tarqatish, ya'ni "atomlar" ga ega bo'lgan o'lchovlar.)
Yuqori nuqtai nazardan guruh belgilar, bu juda mavhumroq, bu barcha o'zboshimchalik tanlovlari yo'qoladi, chunki ushbu maqolaning keyingi qismida, funktsiyani Fourier konvertatsiya qilish tushunchasini mahalliy ixcham Abeliya guruhi.
Bir xil uzluksizlik va Riemann-Lebesg lemmasi

Furye konvertatsiyasi ba'zi hollarda integrallanmaydigan funktsiyalar uchun aniqlanishi mumkin, ammo integral funktsiyalarning Furye konvertatsiyalari bir nechta kuchli xususiyatlarga ega.
Furye konvertatsiyasi f̂ har qanday integral funktsiya f bu bir xilda uzluksiz va[14]
Tomonidan Riemann-Lebesgue lemma,[15]
Biroq, birlashtirilishi shart emas. Masalan, ning Fourier konvertatsiyasi to'rtburchaklar funktsiya, bu ajralmas, bu sinc funktsiyasi, bu emas Lebesgue integral, chunki uning noto'g'ri integrallar ga o'xshash harakat qilish o'zgaruvchan harmonik qatorlar, bo'lmasdan yig'indiga aylantirishda mutlaqo yaqinlashuvchi.
Odatda yozish mumkin emas teskari konvertatsiya kabi Lebesg integrali. Biroq, ikkalasi ham qachon f va ajralmas, teskari tenglik
ushlab turadi deyarli hamma joyda. Ya'ni, Furye konvertatsiyasi in'ektsion kuni L1(ℝ). (Ammo agar shunday bo'lsa f doimiy, keyin har birida tenglik bo'ladi x.)
Plancherel teoremasi va Parseval teoremasi
Ruxsat bering f (x) va g(x) birlashtirilishi mumkin va ruxsat bering f̂ (ξ) va ĝ(ξ) ularning Fourier konvertatsiyalari bo'ling. Agar f (x) va g(x) ham kvadrat bilan birlashtirilishi mumkin, keyin Parseval formulasi quyidagicha:[16]
bu erda bar belgilanadi murakkab konjugatsiya.
The Plancherel teoremasiYuqorida aytilganlardan kelib chiqadigan narsa[17]
Plancherel teoremasi Furye konvertatsiyasini uzluksizlik argumenti bilan a ga qadar kengaytirishga imkon beradi unitar operator kuni L2(ℝ). Yoqilgan L1(ℝ) ∩ L2(ℝ), bu kengaytma aniqlangan Fourier konvertatsiyasiga mos keladi L1(ℝ)Shunday qilib, Fourier konvertatsiyasining domenini kattalashtirish L1(ℝ) + L2(ℝ) (va natijada Lp(ℝ) uchun 1 ≤ p ≤ 2). Plancherel teoremasi Furye konvertatsiyasi saqlaydigan fanlarda izohlanadi energiya asl miqdor. Ushbu formulalar terminologiyasi juda standartlashtirilmagan. Parseval teoremasi faqat Furye seriyasida isbotlangan va uni Lyapunov birinchi marta isbotlagan. Ammo Parseval formulasi Furye konvertatsiyasi uchun ham mantiqan to'g'ri keladi va shuning uchun ham Furye konvertatsiyasi doirasida uni Plancherel isbotlagan bo'lsa ham, uni ko'pincha Parseval formulasi yoki Parseval munosabati, hatto Parseval teoremasi deb atashadi.
Qarang Pontryagin ikkilik mahalliy ixcham abeliya guruhlari sharoitida ushbu kontseptsiyani umumiy shakllantirish uchun.
Puasson yig'indisi formulasi
Puasson yig'indisi formulasi (PSF) bu bilan bog'liq bo'lgan tenglama Fourier seriyasi ning koeffitsientlari davriy yig'ish funktsiyani funktsiyaning uzluksiz Furye konvertatsiyasining qiymatlariga. Puasson yig'indisi formulasida aytilganidek, muntazam funktsiyalar uchun f,
Furye konvertatsiyasining masshtablash va vaqtni almashtirish xususiyatlarini qo'llash orqali asosiy shakllardan kelib chiqadigan turli xil foydali shakllarga ega. Formulada muhandislik, fizika va sonlar nazariyasi. Standart Poisson yig'indisi formulasining chastota-domen duali ham deyiladi diskret vaqtdagi Furye konvertatsiyasi.
Puasson summasi odatda davriy muhit fizikasi bilan bog'liq, masalan, aylana bo'ylab issiqlik o'tkazuvchanligi. Issiqlik tenglamasining aylana ustidagi asosiy echimi a deb ataladi teta funktsiyasi. Bu ishlatiladi sonlar nazariyasi ning bir turi bo'lib chiqadigan teta funktsiyalarining transformatsion xususiyatlarini isbotlash modulli shaklva u umuman nazariyasiga bog'liqdir avtomorf shakllar qaerda u bir tomonida paydo bo'ladi Selberg iz formulasi.
Differentsiya
Aytaylik f (x) mutlaqo uzluksiz farqlanadigan funktsiya va ikkalasi ham f va uning hosilasi f ′ birlashtirilishi mumkin. Keyin hosilaning Furye konvertatsiyasi quyidagicha berilgan
Umuman olganda, ning Fourier konvertatsiyasi nlotin f(n) tomonidan berilgan
Furye konvertatsiyasini qo'llagan holda va ushbu formulalardan foydalangan holda, ba'zilari oddiy differentsial tenglamalar echish ancha oson bo'lgan algebraik tenglamalarga aylantirilishi mumkin. Ushbu formulalar ham bosh barmoq qoidasini keltirib chiqaradi "f (x) silliq agar va faqat agar f̂ (ξ) tezda 0 ga tushadi |ξ| → ∞"Teskari Furye konvertatsiyasi uchun o'xshash qoidalardan foydalangan holda, shuni ham aytish mumkin"f (x) tezda 0 ga tushadi |x| → ∞ agar va faqat agar f̂ (ξ) silliq. "
Konvolyutsiya teoremasi
Fourier konvertatsiyasi o'rtasida tarjima qilinadi konversiya va funktsiyalarni ko'paytirish. Agar f (x) va g(x) Fourier transformatsiyalari bilan integral funktsiyalardir f̂ (ξ) va ĝ(ξ) tegishlicha, u holda konvolyutsiyaning Furye konvertatsiyasi Furye konversiyasining hosilasi bilan beriladi f̂ (ξ) va ĝ(ξ) (Furye konvertatsiyasini aniqlash bo'yicha boshqa konventsiyalar bo'yicha doimiy omil paydo bo'lishi mumkin).
Bu shuni anglatadiki, agar:
qayerda ∗ konvolyutsiya operatsiyasini bildiradi, keyin:
Yilda chiziqli vaqt o'zgarmas (LTI) tizim nazariyasi, talqin qilish odatiy holdir g(x) sifatida impulsli javob kirish bilan LTI tizimining f (x) va chiqish h(x), o'rniga birlik impulsi uchun f (x) hosil h(x) = g(x). Ushbu holatda, ĝ(ξ) ifodalaydi chastotali javob tizimning.
Aksincha, agar f (x) ikkita kvadrat integral funktsiyalar mahsuloti sifatida ajralib chiqishi mumkin p(x) va q(x), keyin Fourier konvertatsiyasi f (x) tegishli Furye konvertatsiyasining konvolusi bilan berilgan p̂(ξ) va q̂(ξ).
O'zaro bog'liqlik teoremasi
Shunga o'xshash tarzda, agar buni ko'rsatsa bo'ladi h(x) bo'ladi o'zaro bog'liqlik ning f (x) va g(x):
keyin Fourier konvertatsiyasi h(x) bu:
Maxsus holat sifatida avtokorrelyatsiya funktsiyasi f (x) bu:
buning uchun
O'ziga xos funktsiyalar
Ortonormal asosning muhim tanlovlaridan biri L2(ℝ) Hermit funktsiyalari bilan berilgan
qayerda Un(x) "probabilistlar" Hermit polinomlarisifatida belgilanadi
Furye konvertatsiyasi bo'yicha ushbu konvensiyaga binoan bizda shunday narsa bor
- .
Boshqacha qilib aytganda, Hermit funktsiyalari to'liqni tashkil qiladi ortonormal tizimi o'ziga xos funktsiyalar Fourier konvertatsiyasi uchun L2(ℝ).[13] Biroq, bu o'ziga xos funktsiyalarni tanlash noyob emas. Faqat to'rt xil o'zgacha qiymatlar Fourier konvertatsiyasining (± 1 va ±)men) va o'ziga xos qiymati bir xil bo'lgan xususiy funktsiyalarning har qanday chiziqli birikmasi boshqa o'ziga xos funktsiyani beradi. Buning natijasida parchalanish mumkin L2(ℝ) to'rtta bo'shliqning to'g'ridan-to'g'ri yig'indisi sifatida H0, H1, H2va H3 bu erda Furye konvertatsiyasi ishlaydi Uk shunchaki tomonidan ko'paytish orqali menk.
Hermite funktsiyalarining to'liq to'plami identifikatsiyani aniqligini ta'minlaganligi sababli, Furye konvertatsiyasi yuqoridagi xususiy qiymatlar bilan tortilgan atamalarning bunday yig'indisi bilan ifodalanishi mumkin va bu yig'indilar aniq ifodalanishi mumkin. Furye konvertatsiyasini aniqlash uchun ushbu yondashuv birinchi bo'lib amalga oshirildi Norbert Viner.[18] Boshqa xususiyatlar qatori, Hermite funktsiyalari ham chastota, ham vaqt oralig'ida tez sur'atlarda pasayib boradi va shu bilan ular Furye konvertatsiyasini umumlashtirishni, ya'ni kasrli Furye konvertatsiyasi vaqt chastotasi tahlilida ishlatiladi.[19] Yilda fizika, ushbu konvertatsiya tomonidan kiritilgan Edvard Kondon.[20]
Heisenberg guruhi bilan aloqa
The Heisenberg guruhi aniq guruh ning unitar operatorlar ustida Hilbert maydoni L2(ℝ) kvadrat birlashtiriladigan murakkab qiymatli funktsiyalar f tarjimalar tomonidan yaratilgan haqiqiy chiziqda (Ty f )(x) = f (x + y) va tomonidan ko'paytma e2πixξ, (Mξ f )(x) = e2πixξ f (x). Ushbu operatorlar o'zlarining (guruh) kommutatorlari bo'lgani kabi qatnovni amalga oshirmaydilar
bu doimiyga ko'paytiriladi (ga bog'liq emas x) e2πiyξ ∈ U(1) (the doira guruhi kompleks modullarning birlik moduli). Abstrakt guruh sifatida Geyzenberg guruhi uch o'lchovli Yolg'on guruh uchtadan (x, ξ, z) ∈ ℝ2 × U(1), guruh qonuni bilan
Heisenberg guruhini belgilang H1. Yuqoridagi protsedura nafaqat guruh tuzilishini, balki standartni ham tavsiflaydi unitar vakillik ning H1 biz belgilaydigan Hilbert makonida r : H1 → B(L2(ℝ)). Ning chiziqli avtomorfizmini aniqlang ℝ2 tomonidan
Shuning uchun; ... uchun; ... natijasida J2 = −Men. Bu J ning noyob avtomorfizmiga qadar kengaytirilishi mumkin H1:
Ga ko'ra Stoun-fon Neyman teoremasi, unitar vakolatxonalar r va r ∘ j bir-biriga tengdir, shuning uchun noyob aralashuvchi mavjud V ∈ U(L2(ℝ)) shu kabi
Ushbu operator V Fourier konvertatsiyasi.
Furye konvertatsiyasining ko'plab standart xususiyatlari bu umumiy ramkaning bevosita natijalaridir.[21] Masalan, Furye konversiyasining kvadrati, V2, bilan bog'liq bo'lgan intertwiner J2 = −Menva shuning uchun bizda bor (V2f )(x) = f (−x) asl funktsiyasining aksidir f.
Kompleks domen
The ajralmas Fourier konvertatsiyasi uchun
uchun o'rganish mumkin murakkab uning argumenti qiymatlari ξ. Xususiyatlariga qarab f, bu haqiqiy o'qdan umuman yaqinlashmasligi yoki a ga yaqinlashishi mumkin murakkab analitik funktsiya ning barcha qiymatlari uchun ξ = σ + iτ, yoki biron bir narsa.[22]
The Peyli-Viyner teoremasi buni aytadi f silliq (ya'ni, n- barcha musbat butun sonlar uchun farqlanadigan vaqtlar n) va agar shunday bo'lsa, ixcham qo'llab-quvvatlanadi f̂ (σ + iτ) a holomorfik funktsiya buning uchun mavjud bo'lgan a doimiy a > 0 har qanday kishi uchun tamsayı n ≥ 0,
ba'zi bir doimiy uchun C. (Ushbu holatda, f yoqilgan [−a, a].) Buni shu bilan ifodalash mumkin f̂ bu butun funktsiya qaysi tez kamayib boradi yilda σ (sobit uchun τ) va eksponent o'sish τ (bir xilda σ).[23]
(Agar f silliq emas, lekin faqat L2, bayonot hanuzgacha taqdim etilgan n = 0.[24]) A ning bunday funktsiyalarining maydoni murakkab o'zgaruvchi Paley - Wiener maydoni deb nomlanadi. Ushbu teorema yarim sodda qilib umumlashtirildi Yolg'on guruhlar.[25]
Agar f yarim chiziqda qo'llab-quvvatlanadi t ≥ 0, keyin f "sabab" deb aytiladi, chunki impulsga javob berish funktsiyasi jismonan amalga oshiriladigan filtr ushbu xususiyatga ega bo'lishi kerak, chunki hech qanday ta'sir uning sababidan oldin turolmaydi. Paley va Wiener shunda ko'rsatdi f̂ a ga qadar uzaytiriladi holomorfik funktsiya murakkab pastki yarim tekislikda τ < 0 kabi nolga intiladi τ cheksizlikka boradi.[26] The converse is false and it is not known how to characterise the Fourier transform of a causal function.[27]
Laplasning o'zgarishi
The Fourier transform f̂ (ξ) bilan bog'liq Laplasning o'zgarishi F(s), which is also used for the solution of differentsial tenglamalar va ning tahlili filtrlar.
It may happen that a function f for which the Fourier integral does not converge on the real axis at all, nevertheless has a complex Fourier transform defined in some region of the murakkab tekislik.
Masalan, agar f (t) is of exponential growth, i.e.,
for some constants C, a ≥ 0, keyin[28]
convergent for all 2πτ < −a, bo'ladi two-sided Laplace transform ning f.
The more usual version ("one-sided") of the Laplace transform is
Agar f is also causal, then
Thus, extending the Fourier transform to the complex domain means it includes the Laplace transform as a special case—the case of causal functions—but with the change of variable s = 2πiξ.
Inversiya
Agar f̂ is complex analytic for a ≤ τ ≤ b, keyin
tomonidan Koshining integral teoremasi. Therefore, the Fourier inversion formula can use integration along different lines, parallel to the real axis.[29]
Theorem: If f (t) = 0 uchun t < 0va |f (t)| < Cea|t| for some constants C, a > 0, keyin
har qanday kishi uchun τ < −a/2π.
This theorem implies the Mellin inversion formula for the Laplace transformation,[28]
har qanday kishi uchun b > a, qayerda F(s) is the Laplace transform of f (t).
The hypotheses can be weakened, as in the results of Carleman and Hunt, to f (t) e−da bo'lish L1, provided that f is of bounded variation in a closed neighborhood of t (qarang Dirichlet-Dini theorem), the value of f da t is taken to be the o'rtacha arifmetik of the left and right limits, and provided that the integrals are taken in the sense of Cauchy principal values.[30]
L2 versions of these inversion formulas are also available.[31]
Fourier transform on Euclidean space
The Fourier transform can be defined in any arbitrary number of dimensions n. As with the one-dimensional case, there are many conventions. For an integrable function f (x), this article takes the definition:
qayerda x va ξ bor n- o'lchovli vektorlarva x · ξ bo'ladi nuqta mahsuloti of the vectors. Shu bilan bir qatorda, ξ can be viewed as belonging to the ikkilangan vektor maydoni , in which case the dot product becomes the qisqarish ning x va ξ, odatda sifatida yoziladi ⟨x, ξ⟩.
All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann-Lebesgue lemma ushlab turadi.[15]
Noaniqlik printsipi
Generally speaking, the more concentrated f (x) is, the more spread out its Fourier transform f̂ (ξ) must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we squeeze a function in x, its Fourier transform stretches out in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.
The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an noaniqlik printsipi by viewing a function and its Fourier transform as conjugate variables ga nisbatan simpektik shakl ustida time–frequency domain: from the point of view of the linear canonical transformation, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the simpektik shakl.
Aytaylik f (x) is an integrable and kvadrat bilan birlashtirilishi mumkin funktsiya. Without loss of generality, assume that f (x) is normalized:
Dan kelib chiqadi Plancherel teoremasi bu f̂ (ξ) is also normalized.
The spread around x = 0 may be measured by the dispersion about zero[32] tomonidan belgilanadi
In probability terms, this is the ikkinchi lahza ning |f (x)|2 about zero.
The uncertainty principle states that, if f (x) is absolutely continuous and the functions x·f (x) va f ′(x) are square integrable, then[13]
- .
The equality is attained only in the case
qayerda σ > 0 is arbitrary and C1 = 4√2/√σ Shuning uchun; ... uchun; ... natijasida f bu L2-normalized.[13] In other words, where f is a (normalized) Gauss funktsiyasi with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance σ−2.
In fact, this inequality implies that:
har qanday kishi uchun x0, ξ0 ∈ ℝ.[12]
Yilda kvant mexanikasi, momentum va pozitsiyasi to'lqin funktsiyalari are Fourier transform pairs, to within a factor of Plankning doimiysi. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg noaniqlik printsipi.[33]
A stronger uncertainty principle is the Hirschman uncertainty principle, which is expressed as:
qayerda H(p) bo'ladi differentsial entropiya ning ehtimollik zichligi funktsiyasi p(x):
where the logarithms may be in any base that is consistent. The equality is attained for a Gaussian, as in the previous case.
Sinus va kosinus o'zgarishi
Fourier's original formulation of the transform did not use complex numbers, but rather sines and cosines. Statisticians and others still use this form. An absolutely integrable function f for which Fourier inversion holds good can be expanded in terms of genuine frequencies (avoiding negative frequencies, which are sometimes considered hard to interpret physically[34]) λ tomonidan
This is called an expansion as a trigonometric integral, or a Fourier integral expansion. The coefficient functions a va b can be found by using variants of the Fourier cosine transform and the Fourier sine transform (the normalisations are, again, not standardised):
va
Older literature refers to the two transform functions, the Fourier cosine transform, a, and the Fourier sine transform, b.
Funktsiya f can be recovered from the sine and cosine transform using
together with trigonometric identities. This is referred to as Fourier's integral formula.[28][35][36][37]
Sferik harmonikalar
Let the set of bir hil harmonik polinomlar daraja k kuni ℝn be denoted by Ak. To'plam Ak iborat solid spherical harmonics daraja k. The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Xususan, agar f (x) = e−π|x|2P(x) kimdir uchun P(x) yilda Ak, keyin f̂ (ξ) = men−k f (ξ). Let the set Hk be the closure in L2(ℝn) of linear combinations of functions of the form f (|x|)P(x) qayerda P(x) ichida Ak. Bo'sh joy L2(ℝn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk.[15]
Ruxsat bering f (x) = f0(|x|)P(x) (bilan P(x) yilda Ak), keyin
qayerda
Bu yerda Jn + 2k − 2/2 belgisini bildiradi Bessel funktsiyasi of the first kind with order n + 2k − 2/2. Qachon k = 0 this gives a useful formula for the Fourier transform of a radial function.[38] This is essentially the Hankel konvertatsiyasi. Moreover, there is a simple recursion relating the cases n + 2 va n[39] allowing to compute, e.g., the three-dimensional Fourier transform of a radial function from the one-dimensional one.
Restriction problems
In higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general sinf of square integrable functions. As such, the restriction of the Fourier transform of an L2(ℝn) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in Lp uchun 1 < p < 2. Surprisingly, it is possible in some cases to define the restriction of a Fourier transform to a set S, taqdim etilgan S has non-zero curvature. Ish qachon S is the unit sphere in ℝn is of particular interest. In this case the Tomas–Shteyn restriction theorem states that the restriction of the Fourier transform to the unit sphere in ℝn is a bounded operator on Lp taqdim etilgan 1 ≤ p ≤ 2n + 2/n + 3.
One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets ER tomonidan indekslangan R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R. For a given integrable function f, consider the function fR tomonidan belgilanadi:
Suppose in addition that f ∈ Lp(ℝn). Uchun n = 1 va 1 < p < ∞, if one takes ER = (−R, R), keyin fR ga yaqinlashadi f yilda Lp kabi R tends to infinity, by the boundedness of the Hilbert o'zgarishi. Naively one may hope the same holds true for n > 1. Bunday holda ER is taken to be a cube with side length R, then convergence still holds. Another natural candidate is the Euclidean ball ER = {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in Lp(ℝn). Uchun n ≥ 2 it is a celebrated theorem of Charlz Fefferman that the multiplier for the unit ball is never bounded unless p = 2.[18] In fact, when p ≠ 2, this shows that not only may fR fail to converge to f yilda Lp, but for some functions f ∈ Lp(ℝn), fR is not even an element of Lp.
Fourier transform on function spaces
Yoqilgan Lp bo'shliqlar
Yoqilgan L1
The definition of the Fourier transform by the integral formula
is valid for Lebesgue integrable functions f; anavi, f ∈ L1(ℝn).
The Fourier transform F : L1(ℝn) → L∞(ℝn) a chegaralangan operator. This follows from the observation that
which shows that its operator normasi is bounded by 1. Indeed, it equals 1, which can be seen, for example, from the transform of the rect function. Ning tasviri L1 is a subset of the space C0(ℝn) of continuous functions that tend to zero at infinity (the Riemann-Lebesgue lemma), although it is not the entire space. Indeed, there is no simple characterization of the image.
Yoqilgan L2
Since compactly supported smooth functions are integrable and dense in L2(ℝn), Plancherel teoremasi allows us to extend the definition of the Fourier transform to general functions in L2(ℝn) by continuity arguments. The Fourier transform in L2(ℝn) is no longer given by an ordinary Lebesgue integral, although it can be computed by an improper integral, here meaning that for an L2 funktsiya f,
where the limit is taken in the L2 sezgi. (More generally, you can take a sequence of functions that are in the intersection of L1 va L2 and that converges to f ichida L2-norm, and define the Fourier transform of f sifatida L2 -limit of the Fourier transforms of these functions.[40])
Many of the properties of the Fourier transform in L1 carry over to L2, by a suitable limiting argument.
Bundan tashqari, F : L2(ℝn) → L2(ℝn) a unitar operator.[41] For an operator to be unitary it is sufficient to show that it is bijective and preserves the inner product, so in this case these follow from the Fourier inversion theorem combined with the fact that for any f, g ∈ L2(ℝn) bizda ... bor
In particular, the image of L2(ℝn) is itself under the Fourier transform.
Boshqa tomondan Lp
The definition of the Fourier transform can be extended to functions in Lp(ℝn) uchun 1 ≤ p ≤ 2 by decomposing such functions into a fat tail part in L2 plus a fat body part in L1. In each of these spaces, the Fourier transform of a function in Lp(ℝn) ichida Lq(ℝn), qayerda q = p/p − 1 is the Hölder conjugate of p (tomonidan Hausdorff - Yosh tengsizlik). However, except for p = 2, the image is not easily characterized. Further extensions become more technical. The Fourier transform of functions in Lp for the range 2 < p < ∞ requires the study of distributions.[14] In fact, it can be shown that there are functions in Lp bilan p > 2 so that the Fourier transform is not defined as a function.[15]
Tempered distributions
One might consider enlarging the domain of the Fourier transform from L1 + L2 by considering generalized functions, or distributions. Tarqatish ℝn is a continuous linear functional on the space Cv(ℝn) of compactly supported smooth functions, equipped with a suitable topology. The strategy is then to consider the action of the Fourier transform on Cv(ℝn) and pass to distributions by duality. The obstruction to doing this is that the Fourier transform does not map Cv(ℝn) ga Cv(ℝn). In fact the Fourier transform of an element in Cv(ℝn) can not vanish on an open set; see the above discussion on the uncertainty principle. The right space here is the slightly larger space of Shvarts vazifalari. The Fourier transform is an automorphism on the Schwartz space, as a topological vector space, and thus induces an automorphism on its dual, the space of tempered distributions.[15] The tempered distributions include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support.
For the definition of the Fourier transform of a tempered distribution, let f va g be integrable functions, and let f̂ va ĝ be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula,[15]
Every integrable function f defines (induces) a distribution Tf munosabat bilan
Shvartsning barcha funktsiyalari uchun φ. So it makes sense to define Fourier transform T̂f ning Tf tomonidan
Shvartsning barcha funktsiyalari uchun φ. Extending this to all tempered distributions T gives the general definition of the Fourier transform.
Distributions can be differentiated and the above-mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.
Umumlashtirish
Fourier–Stieltjes transform
The Fourier transform of a finite Borel measure m kuni ℝn tomonidan berilgan:[42]
This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann-Lebesgue lemma fails for measures.[14] Bunday holda dm = f (x) dx, then the formula above reduces to the usual definition for the Fourier transform of f. Bunday holda m is the probability distribution associated to a random variable X, the Fourier–Stieltjes transform is closely related to the xarakterli funktsiya, but the typical conventions in probability theory take eixξ o'rniga e−2πixξ.[13] In the case when the distribution has a ehtimollik zichligi funktsiyasi this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.
The Fourier transform may be used to give a characterization of measures. Bochner teoremasi characterizes which functions may arise as the Fourier–Stieltjes transform of a positive measure on the circle.[14]
Bundan tashqari, Dirac delta funktsiyasi, although not a function, is a finite Borel o'lchovi. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).
Locally compact abelian groups
The Fourier transform may be generalized to any locally compact abelian group. A locally compact abelian group is an abeliy guruhi that is at the same time a mahalliy ixcham Hausdorff topological space so that the group operation is continuous. Agar G is a locally compact abelian group, it has a translation invariant measure m, deb nomlangan Haar o'lchovi. For a locally compact abelian group G, the set of irreducible, i.e. one-dimensional, unitary representations are called its belgilar. With its natural group structure and the topology of pointwise convergence, the set of characters Ĝ is itself a locally compact abelian group, called the Pontryagin dual ning G. Funktsiya uchun f yilda L1(G), its Fourier transform is defined by[14]
Bu holda Riemann-Lebesgue lemmasi amal qiladi; f̂ (ξ) - bu abadiylikda yo'q bo'lib ketadigan funktsiya Ĝ.
Fourier konvertatsiya qilinadi T= R / Z - bu misol; Bu yerga T mahalliy ixcham abeliya guruhi va Haar o'lchovidir m kuni T [0,1] bo'yicha Lebesg o'lchovi sifatida qaralishi mumkin. Ning vakilligini ko'rib chiqing T murakkab tekislikda C bu 1 o'lchovli murakkab vektor maydoni. Bir guruh vakolatxonalar mavjud (ular beri kamaytirilmaydi) C 1 xira) qayerda uchun .
Bunday vakillikning xarakteri, ya'ni izidir har biriga va , bo'ladi o'zi. Cheklangan guruhning vakili bo'lsa, guruhning belgilar jadvali G vektorlarning satrlari bo'lib, har bir satr bitta qisqartirilmaydigan tasvirning belgisidir G, va bu vektorlar xaritadan sinf funktsiyalari makonining ortonormal asosini tashkil qiladi G ga C Schur lemma bilan. Endi guruh T endi cheklangan emas, lekin hali ham ixcham va u belgilar jadvali ortonomalligini saqlaydi. Jadvalning har bir qatori funktsiyadir ning va ikkita sinf funktsiyalari orasidagi ichki mahsulot (barcha funktsiyalar buyon sinf funktsiyalari T abeliya) f, sifatida belgilanadi normalizatsiya qiluvchi omil bilan Ketma-ketlik sinf funktsiyalari makonining ortonormal asosidir
Har qanday vakillik uchun V cheklangan guruh G, span sifatida ifodalanishi mumkin ( ning irrepslari G), s.t . Xuddi shunday va , . Pontriagin duali bu va uchun , uning Fourier konvertatsiyasi .
Gelfand o'zgarishi
Fourier konvertatsiyasi, shuningdek, Gelfand o'zgarishi. Ushbu alohida kontekstda u yuqorida belgilangan Pontryagin ikkilik xaritasi bilan chambarchas bog'liqdir.
Abeliya berilgan mahalliy ixcham Hausdorff topologik guruh G, oldingi kabi, biz bo'shliqni ko'rib chiqamiz L1(G), Haar o'lchovi yordamida aniqlangan. Ko'payish kabi konvulsiya bilan, L1(G) abeliyalik Banach algebra. Unda ham bor involyutsiya * tomonidan berilgan
Mumkin bo'lgan eng katta hajmdagi ishni bajarish C*-norm o'zining konvertini beradi C*-algebra, guruh deb nomlangan C*-algebra C*(G) ning G. (Har qanday C*-norm yoqilgan L1(G) bilan chegaralanadi L1 norma, shuning uchun ularning supremumi mavjud.)
Har qanday abeliya berilgan C*-algebra A, Gelfand konvertatsiyasi orasidagi izomorfizmni beradi A va C0(A^), qayerda A^ multiplikativ chiziqli funktsionallar, ya'ni bir o'lchovli tasvirlar, bo'yicha A zaif bilan * topologiya. Xarita oddiygina tomonidan berilgan
Ning multiplikativ chiziqli funksionallari chiqadi C*(G), mos identifikatsiyadan so'ng, aniq belgilar G, va Gelfand o'zgaradi, agar zich ichki qism bilan cheklangan bo'lsa L1(G) bu Furye-Pontryagin o'zgarishi.
Abeliya bo'lmagan ixcham guruhlar
Furye konvertatsiyasini abeliya bo'lmagan guruhdagi funktsiyalar uchun ham aniqlash mumkin, agar guruh bo'lsa ixcham. Asosiy guruh abeliya degan tushunchani olib tashlash, kamaytirilmaydigan unitar vakillar har doim ham bir o'lchovli bo'lishi shart emas. Demak, abelian bo'lmagan guruhdagi Furye konvertatsiyasi qiymatlarni Xilbert kosmik operatorlari sifatida qabul qiladi.[43] Furye konvertatsiyasi ixcham guruhlar uchun asosiy vosita hisoblanadi vakillik nazariyasi[44] va komutativ bo'lmagan harmonik tahlil.
Ruxsat bering G ixcham bo'ling Hausdorff topologik guruh. Ruxsat bering Σ cheklangan o'lchovli barcha izomorfizm sinflari to'plamini belgilang unitar vakolatxonalar, vakillikning aniq tanlovi bilan birga U(σ) ustida Hilbert maydoni Hσ cheklangan o'lchov dσ har biriga σ ∈ Σ. Agar m cheklangan Borel o'lchovi kuni G, keyin Fourier-Stieltjes konvertatsiyasi m operator yoqilgan Hσ tomonidan belgilanadi
qayerda U(σ) ning murakkab-konjuge vakili hisoblanadi U(σ) harakat qilish Hσ. Agar m bu mutlaqo uzluksiz ga nisbatan chap-o'zgarmas ehtimollik o'lchovi λ kuni G, vakili kabi
kimdir uchun f ∈ L1(λ), ning Fourier konvertatsiyasini aniqlaydi f ning Fourier-Stieltjes konvertatsiyasi bilan m.
Xaritalash
orasidagi izomorfizmni belgilaydi Banach maydoni M(G) cheklangan Borel o'lchovlari (qarang bo'sh joy) va Banax makonining yopiq subspace C∞(Σ) barcha ketma-ketliklardan iborat E = (Eσ) tomonidan indekslangan Σ (chegaralangan) chiziqli operatorlar Eσ : Hσ → Hσ buning uchun norma
cheklangan. "konvulsiya teoremasi"bundan tashqari, Banax bo'shliqlarining bu izomorfizmi aslida izometrik izomorfizmidir C * algebralar ning subspace-ga C∞(Σ). Ko'paytirish yoqilgan M(G) tomonidan berilgan konversiya chora-tadbirlar va involution * tomonidan belgilanadi
va C∞(Σ) tabiiyga ega C*-algebra tuzilishi, Hilbert fazoviy operatorlari sifatida.
The Piter-Veyl teoremasi ushlab turadi va Furye inversiya formulasining versiyasi (Plancherel teoremasi) quyidagicha: agar f ∈ L2(G), keyin
bu erda yig'indisi konvergent sifatida tushuniladi L2 sezgi.
Furye konvertatsiyasini umumiy bo'lmagan holatga umumlashtirish, qisman rivojlanishiga hissa qo'shdi noaniq geometriya.[iqtibos kerak] Shu nuqtai nazardan, Furye konversiyasining nodavlat guruhlarga kategorik ravishda umumlashtirilishi Tannaka - Kerin ikkiligi, bu belgilar guruhini vakolatxonalar toifasiga almashtiradi. Biroq, bu harmonik funktsiyalar bilan aloqani yo'qotadi.
Shu bilan bir qatorda
Yilda signallarni qayta ishlash atamalar, funktsiya (vaqt) - bu signalning mukammal bilan ifodalanishi vaqtni aniqlash, ammo Fourier konvertatsiyasi mukammal bo'lsa-da, chastota haqida ma'lumot yo'q chastota o'lchamlari, ammo vaqt haqida ma'lumot yo'q: Furye konvertatsiyasining kattaligi bir nuqtada qancha chastota tarkibiga ega, lekin joylashish faqat faza bilan beriladi (Furye transformatsiyasining nuqtadagi argumenti) va turgan to'lqinlar o'z vaqtida lokalizatsiya qilinmagan - sinus to'lqin parchalanmasdan cheksizgacha davom etadi. Bu Fourier konvertatsiyasining vaqt ichida lokalizatsiya qilingan signallarni tahlil qilish uchun foydaliligini cheklaydi, xususan vaqtinchalikyoki cheklangan darajadagi har qanday signal.
Furye konvertatsiyasiga alternativ sifatida, yilda vaqt chastotasini tahlil qilish, signallarni bir muncha vaqt ma'lumotlari va ba'zi bir chastota ma'lumotlariga ega bo'lgan shaklda namoyish qilish uchun vaqt chastotasi o'zgarishi yoki vaqt chastotasi taqsimotidan foydalaniladi - noaniqlik printsipiga ko'ra, bular o'rtasida kelishuv mavjud. Ular Fourier konvertatsiyasining umumlashtirilishi bo'lishi mumkin, masalan qisqa vaqt ichida Fourier konvertatsiyasi yoki kasrli Furye konvertatsiyasiyoki kabi signallarni aks ettirish uchun boshqa funktsiyalar dalgalanma o'zgaradi va chirplet o'zgaradi, Fourier konvertatsiyasining to'lqinli analogi bilan (doimiy) uzluksiz to'lqin o'zgarishi.[19]
Ilovalar
Differentsial tenglamalarni tahlil qilish
Ehtimol, Furye transformatsiyasining eng muhim ishlatilishi hal qilishdir qisman differentsial tenglamalar.XX asr matematik fizikasining ko'plab tenglamalariga shunday munosabatda bo'lish mumkin. Furye bir o'lchovda va o'lchovsiz birliklarda bo'lgan issiqlik tenglamasini o'rgangan
Biz keltiradigan misol, biroz qiyinroq, bir o'lchovdagi to'lqin tenglamasi,
Odatdagidek, muammo echim topishda emas: cheksiz ko'p. Muammo shundaki, "chegara masalasi" deb nomlanadi: "chegara shartlari" ni qondiradigan echimni toping
Bu yerda, f va g funktsiyalari berilgan. Issiqlik tenglamasi uchun faqat bitta chegara sharti talab qilinishi mumkin (odatda birinchi). Ammo to'lqin tenglamasi uchun hali ham cheksiz ko'p echimlar mavjud y birinchi chegara shartini qondiradigan. Ammo har ikkala shartni qo'yganda, faqat bitta echim bo'lishi mumkin.
Furye konvertatsiyasini topish osonroq ŷ to'g'ridan-to'g'ri echimni topishdan ko'ra eritmaning. Buning sababi shundaki, Furye konversiyasi differentsiatsiyani Furye-ikkilangan o'zgaruvchiga ko'paytirishga oladi va shuning uchun dastlabki funktsiyaga tatbiq etiladigan qisman differentsial tenglama, o'zgartirilgan funktsiyaga tatbiq etiladigan ikkilamchi o'zgaruvchilarning polinom funktsiyalari bilan ko'paytirilishga aylanadi. Keyin ŷ aniqlandi, topish uchun teskari Furye transformatsiyasini qo'llashimiz mumkin y.
Furye usuli quyidagicha. Birinchidan, shakllarning har qanday funktsiyasiga e'tibor bering
to'lqin tenglamasini qondiradi. Ularga elementar echimlar deyiladi.
Ikkinchidan, har qanday ajralmas narsaga e'tibor bering
(o'zboshimchalik uchun a+, a−, b+, b−) to'lqin tenglamasini qondiradi. (Bu integral faqat uzluksiz chiziqli birikmaning bir turi va tenglama chiziqli).
Endi bu funktsiyaning Furye sintezi formulasiga o'xshaydi. Aslida, bu haqiqiy teskari Fourier konvertatsiyasi a± va b± o'zgaruvchida x.
Uchinchi qadam - o'ziga xos noma'lum koeffitsient funktsiyalarini qanday topish kerakligini tekshirish a± va b± olib keladi y chegara shartlarini qondirish. Ushbu echimlarning qiymatlari bizni qiziqtiradi t = 0. Shunday qilib, biz o'rnatamiz t = 0. Furye inversiyasi uchun zarur bo'lgan shartlar qondirilgan deb hisoblasak, Furye sinusi va kosinus o'zgarishini topish mumkin (o'zgaruvchida x) ikkala tomonning va oling
va
Xuddi shunday, ning hosilasini olish y munosabat bilan t va keyin Furye sinusi va kosinus konvertatsiyasini qo'llang
va
Bu to'rtta noma'lum uchun to'rtta chiziqli tenglama a± va b±, elementar algebra bilan osonlikcha hal qilinadigan chegara shartlarining Furye sinusi va kosinus o'zgarishlari nuqtai nazaridan, bu o'zgarishni topish mumkin.
Xulosa qilib aytganda, biz parametrlangan elementar echimlar to'plamini tanladik ξ, ulardan umumiy echim parametr bo'yicha integral (doimiy) chiziqli kombinatsiya bo'ladi ξ. Ammo bu integral Furye integrali shaklida bo'lgan. Keyingi qadam chegara shartlarini ushbu integrallar bilan ifodalash va ularni berilgan funktsiyalarga tenglashtirish edi f va g. Ammo bu iboralar, shuningdek, hosilaning Furye konvertatsiyasining xususiyatlari tufayli Furye integrali shaklini oldi. Oxirgi qadam, Furye konversiyasini har ikki tomonga tatbiq etish orqali Fourier inversiyasidan foydalanish va shu bilan koeffitsient funktsiyalari uchun iboralarni olish edi. a± va b± berilgan chegara shartlari bo'yicha f va g.
Yuqori nuqtai nazardan, Furye protsedurasini ko'proq kontseptual ravishda o'zgartirish mumkin. Ikki o'zgaruvchi bo'lgani uchun, biz ikkalasida ham Furye transformatsiyasidan foydalanamiz x va t shunchaki fazoviy o'zgaruvchilarni o'zgartirgan Furye kabi ishlashdan ko'ra. Yozib oling ŷ beri tarqatish ma'nosida ko'rib chiqilishi kerak y(x, t) bo'lmaydi L1: to'lqin sifatida, u vaqt o'tishi bilan davom etadi va shuning uchun vaqtinchalik hodisa emas. Ammo u cheklangan bo'ladi va shuning uchun uning Furye konvertatsiyasi taqsimot sifatida aniqlanishi mumkin. Furye transformatsiyasining ushbu tenglamaga taalluqli bo'lgan operatsion xususiyatlari shundaki, u differentsiatsiyani oladi x ga ko'paytirish 2πiξ va nisbatan farqlash t ga ko'paytirish 2πagar qayerda f chastota. Keyin to'lqin tenglamasi in algebraik tenglamaga aylanadi ŷ:
Bu talab bilan tengdir ŷ(ξ, f ) = 0 agar bo'lmasa ξ = ±f. Darhol, bu nima uchun biz ilgari qilgan elementar echimlarni tanlash juda yaxshi ishlaganligini tushuntiradi: aniq f̂ = δ(ξ ± f ) echimlar bo'ladi. Ushbu delta funktsiyalariga Fourier inversiyasini qo'llagan holda, avval tanlagan elementar echimlarni olamiz. Ammo yuqori nuqtai nazardan, oddiy echimlarni tanlamaydi, aksincha (degeneratsiya qilingan) konusda qo'llab-quvvatlanadigan barcha taqsimotlarning maydonini hisobga oladi. ξ2 − f2 = 0.
Biz chiziqdagi bitta o'zgaruvchining taqsimotlari bilan berilgan konusda qo'llab-quvvatlanadigan taqsimotlarni ham ko'rib chiqishimiz mumkin ξ = f qatorda tarqatish ξ = −f quyidagicha: agar ϕ har qanday sinov funktsiyasi,
qayerda s+va s−, bitta o'zgaruvchining taqsimoti.
Keyin Fourier inversiyasi, chegara shartlari uchun, biz yuqorida aniqroq bo'lgan narsalarga juda o'xshash narsani beradi (qo'yilgan) ϕ(ξ, f ) = e2πmen(xξ+tf ), bu aniq polinom o'sishi):
va
Endi, avvalgidek, o'zgaruvchida bir o'zgaruvchili Furye konversiyasini qo'llang x ning bu funktsiyalariga x ikkita noma'lum taqsimotda ikkita tenglama hosil qiladi s± (agar chegara shartlari bo'lsa, bu oddiy funktsiyalar deb qabul qilinishi mumkin L1 yoki L2).
Hisoblash nuqtai nazaridan, albatta, kamchiliklar shundan iboratki, avvalo chegara shartlarining Furye o'zgarishini hisoblash kerak, so'ngra bulardan yechimni yig'ib, so'ngra teskari Furye konvertatsiyasini hisoblash kerak. Yopiq shakl formulalari kamdan-kam uchraydi, faqat geometrik simmetriya ishlatilishi mumkin bo'lgan holatlar bundan mustasno va raqamli hisob-kitoblar qiyin, chunki integrallarning tebranish xarakteri mavjud, bu esa yaqinlashishni sekinlashtiradi va baholashni qiyinlashtiradi. Amaliy hisob-kitoblar uchun ko'pincha boshqa usullardan foydalaniladi.
Yigirmanchi asrda ushbu usullar polinom koeffitsientlari bo'lgan barcha chiziqli qisman differentsial tenglamalarga kengaytirildi va Furye konvertatsiyasi tushunchasini kengaytirib, Furye integral operatorlari, ba'zi chiziqli bo'lmagan tenglamalar ham kiritildi.
Furye transformatsion spektroskopiyasi
Fourier konvertatsiyasi ham ishlatiladi yadro magnit-rezonansi (NMR) va boshqa turlarida spektroskopiya, masalan. infraqizil (FTIR). NMRda vaqt domenida eksponensial shakldagi erkin induksion parchalanish (FID) signali olinadi va Furye chastota domenida Lorentsiya chizig'i shakliga aylanadi. Fourier konvertatsiyasi ham ishlatiladi magnit-rezonans tomografiya (MRI) va mass-spektrometriya.
Kvant mexanikasi
Fourier konvertatsiyasi foydalidir kvant mexanikasi ikki xil usulda. Dastlab, kvant mexanikasining asosiy kontseptual tuzilishi juftliklarning mavjudligini postulat qiladi bir-birini to'ldiruvchi o'zgaruvchilar, bilan bog'langan Heisenberg noaniqlik printsipi. Masalan, bitta o'lchovda fazoviy o'zgaruvchi q Masalan, zarrachani faqat kvant mexanikasi bilan o'lchash mumkin "pozitsiya operatori"impuls haqida ma'lumotni yo'qotish evaziga p zarrachaning Shuning uchun zarrachaning fizik holatini "to'lqin funktsiyasi" deb nomlangan funktsiya bilan tasvirlash mumkin q yoki funktsiyasi bilan p lekin ikkala o'zgaruvchining funktsiyasi bilan emas. O'zgaruvchan p ga konjugat o'zgaruvchisi deyiladi q. Klassik mexanikada zarrachaning fizik holati (ekspozitsiyaning soddaligi uchun bir o'lchovda mavjud) ikkalasiga ham aniq qiymatlarni berish orqali berilgan bo'lar edi p va q bir vaqtning o'zida. Shunday qilib, barcha mumkin bo'lgan jismoniy holatlarning to'plami $ a $ bo'lgan ikki o'lchovli haqiqiy vektor makonidir p-aksis va a q- eksa fazaviy bo'shliq.
Aksincha, kvant mexanikasi bu bo'shliqning qutblanishini ma'noda tanlaydi, chunki u yarim o'lchovning pastki maydonini tanlaydi, masalan q-aksisitning o'zi, lekin faqat nuqtalarni hisobga olish o'rniga, bu o'qda barcha kompleks qiymatga ega bo'lgan "to'lqin funktsiyalari" to'plamini oladi. Shunga qaramay, ni tanlash p-aksis - bu teng darajada to'g'ri bo'lgan qutblanish, bu zarrachaning mumkin bo'lgan fizik holatlari to'plamining Furye konvertatsiyasi bilan birinchi tasviri bilan bog'liq bo'lgan boshqa ko'rinishini beradi.
Jismoniy jihatdan amalga oshiriladigan holatlar L2va shuning uchun Planxerel teoremasi bo'yicha ularning Fyure o'zgarishlari ham bo'ladi L2. (E'tibor bering, beri q masofa birliklarida va p momentum birliklarida, ko'rsatkichda Plank konstantasining mavjudligi ko'rsatkichni hosil qiladi o'lchovsiz, bo'lishi kerak.)
Shu sababli, Furye konvertatsiyasi zarrachaning holatini aks ettirishning bir usulidan, pozitsiyaning to'lqin funktsiyasi bilan, zarrachaning holatini aks ettirishning boshqa usulidan: impulsning to'lqin funktsiyasi orqali o'tish uchun ishlatilishi mumkin. Cheksiz ko'p turli xil qutblanishlar mumkin va barchasi bir xil kuchga ega. Holatlarni bir vakolatxonadan boshqasiga o'zgartira olish ba'zan qulaydir.
Kvant mexanikasida va boshqa Furye konvertatsiyasidan foydalanish kvant maydon nazariyasi amaldagi to'lqin tenglamasini echishdir. Nisbiy bo'lmagan kvant mexanikasida, Shredinger tenglamasi chunki tashqi kuchlarga bo'ysunmaydigan, bir o'lchovdagi vaqt o'zgaruvchan to'lqin funktsiyasi
Bu xayoliy birlik mavjudligidan tashqari, issiqlik tenglamasi bilan bir xil men. Ushbu tenglamani echishda Fourier usullaridan foydalanish mumkin.
Potentsial energiya funktsiyasi tomonidan berilgan potentsial mavjud bo'lganda V(x), tenglama bo'ladi
Yuqorida aytib o'tganimizdek, "elementar echimlar" zarrachaning "statsionar holatlari" deb nomlanadi va Furye algoritmi, yuqorida tavsiflanganidek, hali ham kelajakdagi evolyutsiyaning chegara muammosini hal qilishda ishlatilishi mumkin. ψ uchun uning qiymatlarini hisobga olgan holda t = 0. Ushbu yondashuvlarning ikkalasi ham kvant mexanikasida amaliy qo'llanilmaydi. Chegaraviy muammolar va to'lqin funktsiyasining vaqt evolyutsiyasi amaliy jihatdan unchalik qiziqtirmaydi: bu harakatsiz holatlar eng muhimi.
Relyativistik kvant mexanikasida Shredinger tenglamasi klassik fizikada odatdagidek to'lqin tenglamasiga aylanadi, faqat murakkab qiymatli to'lqinlar hisobga olinadi. Oddiy misol, boshqa zarralar yoki maydonlar bilan o'zaro aloqalar bo'lmagan taqdirda, erkin o'lchovli Klein-Gordon-Shredinger-Fok tenglamasi, bu safar o'lchovsiz birliklarda,
Bu matematik nuqtai nazardan, klassik fizikaning yuqorida hal qilingan to'lqin tenglamasi bilan bir xil (lekin usullarda farq qilmaydigan murakkab qiymatli to'lqin bilan). Bu kvant maydon nazariyasida juda katta foydalidir: to'lqinning har bir alohida Furye komponenti alohida garmonik osilator sifatida ko'rib chiqilishi va keyinchalik "ikkinchi kvantlash" deb nomlanadigan kvantlashi mumkin. Furye usullari ahamiyatsiz bo'lmagan o'zaro ta'sirlarni hal qilish uchun ham moslashtirilgan.
Signalni qayta ishlash
Furye konvertatsiyasi vaqt qatorlarining spektral tahlili uchun ishlatiladi. Statistik signallarni qayta ishlash predmeti, ammo odatda signalning o'ziga Furye konvertatsiyasini qo'llamaydi. Haqiqiy signal haqiqatan ham o'tkinchi bo'lsa ham, uning xarakteristik xususiyatlari har doim o'zgarmas ekanligi nuqtai nazaridan statsionar bo'lgan funktsiyani (yoki alternativa, stoxastik jarayonni) modellashtirish maqsadga muvofiqdir. Bunday funktsiyani Furye konvertatsiyasi odatdagi ma'noda mavjud emas va buning o'rniga uning avtokorrelyatsiya funktsiyasining Furye konvertatsiyasini olish uchun signallarni tahlil qilish uchun ko'proq foydali deb topildi.
Avtokorrelyatsiya funktsiyasi R funktsiya f bilan belgilanadi
Ushbu funktsiya vaqtni kechiktirish funktsiyasidir τ qiymatlari orasida o'tgan f o'zaro bog'liq bo'lish.
Ko'p funktsiyalar uchun f amalda yuz beradigan, R kechikishning cheklangan juft funktsiyasi τ va odatdagi shovqinli signallar uchun maksimal at bilan bir xil uzluksiz bo'lib chiqadi τ = 0.
Avtokorrelyatsiya funktsiyasi, agar u to'g'ri keladigan darajada normallashtirilmasa, ko'proq to'g'ri deb nomlangan avtokovariantsiya funktsiyasi, qiymatlari o'rtasidagi o'zaro bog'liqlikning kuchini o'lchaydi f vaqt kechikishi bilan ajralib turadi. Bu o'zaro bog'liqlikni izlash usuli f o'z o'tmishi bilan. Bu signallarni tahlil qilishdan tashqari, boshqa statistik vazifalar uchun ham foydalidir. Masalan, agar f (t) vaqtdagi haroratni ifodalaydi t, harorat 24 soatlik kechikish bilan kuchli bog'liqlikni kutmoqda.
U Fourier konvertatsiyasiga ega,
Ushbu Fyurye konvertatsiyasi ning kuch spektral zichligi funktsiyasi deyiladi f. (Agar barcha davriy komponentlar avval filtrlanmagan bo'lsa f, bu integral ajralib chiqadi, ammo bunday davriylikni filtrlash oson.)
Ushbu zichlik funktsiyasi tomonidan ko'rsatilgan quvvat spektri P, ma'lumotlarga ta'sir ko'rsatadigan tafovut miqdorini chastota bo'yicha o'lchaydi ξ. Elektr signallarida dispersiya o'rtacha quvvatga (vaqt birligi uchun energiya) mutanosibdir va shuning uchun quvvat spektri turli chastotalar signalning o'rtacha kuchiga qancha hissa qo'shishini tavsiflaydi. Ushbu jarayon vaqt seriyasining spektral tahlili deb nomlanadi va vaqt qatori bo'lmagan ma'lumotlarning odatdagi dispersiyasini tahliliga o'xshaydi (ANOVA).
Ushbu ma'noda qaysi chastotalarning "muhim" ekanligini bilish filtrlarning to'g'ri dizayni va o'lchov vositalarini to'g'ri baholash uchun juda muhimdir. Ma'lumotlarni ishlab chiqarish uchun mas'ul bo'lgan hodisalarni ilmiy tahlil qilish uchun ham foydali bo'lishi mumkin.
Signalning quvvat spektrini, shuningdek, tor diapazondan tashqaridagi barcha chastotalar filtrlangandan so'ng signalda qoladigan o'rtacha quvvatni o'lchash orqali to'g'ridan-to'g'ri o'lchash mumkin.
Vizual signallar uchun ham spektral tahlil o'tkaziladi. Quvvat spektri barcha fazali munosabatlarni e'tiborsiz qoldiradi, bu ko'p maqsadlar uchun etarlicha yaxshi, ammo video signallari uchun Furye konvertatsiyasini vosita sifatida ishlatib, boshqa spektral tahlil turlari ham qo'llanilishi kerak.
Boshqa yozuvlar
Uchun boshqa keng tarqalgan yozuvlar f̂ (ξ) quyidagilarni o'z ichiga oladi:
Furye konvertatsiyasini o'zgartirilayotgan funktsiya harfiga mos keladigan bosh harf bilan belgilash (masalan f (x) va F(ξ)) ayniqsa fanlar va muhandislikda keng tarqalgan. Elektron, omega (ω) o'rniga ko'pincha ishlatiladi ξ uning burchak chastotasi sifatida talqin qilinishi tufayli ba'zan shunday yoziladi F( jω), qayerda j bo'ladi xayoliy birlikbilan bog'liqligini ko'rsatish uchun Laplasning o'zgarishi, va ba'zan u norasmiy sifatida yoziladi F(2πf ) oddiy chastotadan foydalanish uchun. Zarralar fizikasi kabi ba'zi kontekstlarda xuddi shu belgi funktsiya uchun ham ishlatilishi mumkin, shuningdek Fourier konvertatsiyasi, ikkalasi faqat ular bilan ajralib turadi dalil: momentum argumenti tufayli Fourier konvertatsiyasiga murojaat qiladi, while pozitsion argument tufayli asl funktsiyaga murojaat qiladi. Tiltlar xuddi shunday ishlatilishi mumkin bo'lsa-da Fourier konvertatsiyasini ko'rsatish uchun tildes shuningdek, kattaroq miqdor bilan modifikatsiyani ko'rsatish uchun ishlatilishi mumkin Lorents o'zgarmas kabi shakl , shuning uchun ehtiyot bo'lish kerak.
Murakkab funktsiyani talqini f̂ (ξ) ichida ifodalash orqali yordam berilishi mumkin qutb koordinatasi shakl
ikkita haqiqiy funktsiya nuqtai nazaridan A(ξ) va φ(ξ) qaerda:
bo'ladi amplituda va
bo'ladi bosqich (qarang arg funktsiyasi).
Keyin teskari konvertatsiya yozilishi mumkin:
ning barcha chastota tarkibiy qismlarining rekombinatsiyasi hisoblanadi f (x). Har bir komponent kompleksdir sinusoid shaklning e2πixξ uning amplitudasi A(ξ) va kimning boshlanishi o'zgarishlar burchagi (da x = 0) φ(ξ).
Furye konvertatsiyasini funktsiya bo'shliqlarida xaritalash deb hisoblash mumkin. Ushbu xaritalash bu erda ko'rsatilgan F va F( f ) funktsiyani Furye konvertatsiyasini belgilash uchun ishlatiladi f. Ushbu xaritalash chiziqli bo'lib, bu shuni anglatadiki F shuningdek, funktsiya maydonidagi chiziqli o'zgarish sifatida qaralishi mumkin va vektorga chiziqli transformatsiyani qo'llashning chiziqli algebrasidagi standart yozuv (bu erda funktsiya) f ) yozish uchun ishlatilishi mumkin F f o'rniga F( f ). Furye konvertatsiyasini qo'llash natijasi yana bir funktsiya bo'lgani uchun, biz ushbu funktsiya qiymatiga baholangan qiymat bilan qiziqishimiz mumkin ξ uning o'zgaruvchisi uchun va bu quyidagicha belgilanadi F f (ξ) yoki kabi ( F f )(ξ). E'tibor bering, avvalgi holatda, buni bevosita anglashilgan F birinchi navbatda qo'llaniladi f va keyin olingan funktsiya baholanadi ξ, aksincha emas.
Matematikada va turli amaliy fanlarda ko'pincha funktsiyani farqlash kerak f va qiymati f uning o'zgaruvchisi teng bo'lganda x, belgilangan f (x). Bu degani, shunga o'xshash yozuv F( f (x)) rasmiy ravishda qiymatlarining Furye konvertatsiyasi sifatida talqin qilinishi mumkin f da x. Ushbu kamchilikka qaramay, avvalgi yozuv tez-tez paydo bo'ladi, ko'pincha ma'lum bir funktsiyani yoki ma'lum bir o'zgaruvchining funktsiyasini o'zgartirish kerak bo'lganda. Masalan,
ba'zan a ning Fourier konvertatsiyasini ifodalash uchun ishlatiladi to'rtburchaklar funktsiya a sinc funktsiyasi, yoki
Furye transformatsiyasining siljish xususiyatini ifodalash uchun ishlatiladi.
E'tibor bering, oxirgi misol faqat o'zgartirilgan funktsiya funktsiyasi degan taxmin ostida to'g'ri bo'ladi x, emas x0.
Boshqa anjumanlar
Furye konvertatsiyasi, shuningdek, yozilishi mumkin burchak chastotasi:
kimning birliklari radianlar soniyada
O'zgartirish ξ = ω/2π yuqoridagi formulalar ushbu konventsiyani ishlab chiqaradi:
Ushbu konventsiya bo'yicha teskari konvertatsiya quyidagicha bo'ladi:
Ushbu maqolada keltirilgan konventsiyadan farqli o'laroq, Furye konvertatsiyasi shu tarzda aniqlanganda, u endi a unitar transformatsiya kuni L2(ℝn). Shuningdek, Furye konvertatsiyasi va uning teskari formulalari o'rtasida kamroq simmetriya mavjud.
Yana bir konventsiya - bu omilni ajratishdir (2π)n Furye konvertatsiyasi va uning teskari orasidagi teng ravishda, bu ta'riflarga olib keladi:
Ushbu konventsiyaga ko'ra, Furye konvertatsiyasi yana unitar o'zgarishdir L2(ℝn). Shuningdek, u Furye konvertatsiyasi va uning teskari tomoni o'rtasidagi simmetriyani tiklaydi.
Uchala konvensiyaning o'zgarishi kompleks-eksponentni birlashtirish orqali yaratilishi mumkin yadro oldinga va teskari o'zgarishlarning ham. Belgilar qarama-qarshi bo'lishi kerak. Bundan tashqari, tanlov (yana) konventsiya masalasidir.
| oddiy chastota ξ (Hz) | unitar | |
|---|---|---|
| burchak chastotasi ω (rad / s) | unitar | |
| unitar bo'lmagan |
| oddiy chastota ξ (Hz) | unitar | |
|---|---|---|
| burchak chastotasi ω (rad / s) | unitar | |
| unitar bo'lmagan |
Yuqorida muhokama qilinganidek xarakterli funktsiya tasodifiy o'zgaruvchining qiymati bilan bir xil Fourier-Stieltjes o'zgarishi uning taqsimot o'lchovi, ammo shu nuqtai nazardan doimiylar uchun boshqa konventsiyani qabul qilish odatiy holdir. Odatda xarakterli funktsiya aniqlanadi
Yuqoridagi "unitar bo'lmagan burchak chastotasi" konventsiyasida bo'lgani kabi, 2 omilπ na normallashtiruvchi doimiyda, na ko'rsatkichda ko'rinmaydi. Yuqorida keltirilgan har qanday konventsiyadan farqli o'laroq, ushbu konventsiya ko'rsatkichda qarama-qarshi belgini oladi.
Hisoblash usullari
Tegishli hisoblash usuli asosan asl matematik funktsiya qanday ifodalanishiga va chiqish funktsiyasining kerakli shakliga bog'liq.
Furye konvertatsiyasining asosiy ta'rifi ajralmas bo'lgani uchun, uni quyidagicha ifodalash mumkin funktsiyalar yopiq shakldagi iboralar odatda natija sifatida Fourier konjugat o'zgaruvchisida yopiq shaklli ifodani olish uchun integralni analitik usulda ishlash orqali hisoblashadi. Bu Furye konvertatsiyasining jadvallarini yaratish uchun ishlatiladigan usul,[45] shu jumladan quyidagi jadvalda (Furye konvertatsiyasi # Muhim Furye konvertatsiyasining jadvallari).
Kabi ko'plab kompyuter algebra tizimlari Matlab va Matematik qodir bo'lganlar ramziy integratsiya Fourier konvertatsiyasini analitik ravishda hisoblashga qodir. Masalan, ning Fourier konvertatsiyasini hisoblash uchun f (t) = cos (6πt) e−πt2 buyruqni kiritish mumkin cos (6 * pi * t) exp (−pi * t ^ 2) exp (-i * 2 * pi * f * t) ni -infdan infgacha ichiga Wolfram Alpha.
Yopiq shaklli funktsiyalarning raqamli integratsiyasi
If the input function is in closed-form and the desired output function is a series of ordered pairs (for example a table of values from which a graph can be generated) over a specified domain, then the Fourier transform can be generated by raqamli integratsiya at each value of the Fourier conjugate variable (frequency, for example) for which a value of the output variable is desired.[46] Note that this method requires computing a separate numerical integration for each value of frequency for which a value of the Fourier transform is desired.[47][48] The numerical integration approach works on a much broader class of functions than the analytic approach, because it yields results for functions that do not have closed form Fourier transform integrals.
Tartiblangan juftliklar qatorining sonli integratsiyasi
If the input function is a series of ordered pairs (for example, a time series from measuring an output variable repeatedly over a time interval) then the output function must also be a series of ordered pairs (for example, a complex number vs. frequency over a specified domain of frequencies), unless certain assumptions and approximations are made allowing the output function to be approximated by a closed-form expression. In the general case where the available input series of ordered pairs are assumed be samples representing a continuous function over an interval (amplitude vs. time, for example), the series of ordered pairs representing the desired output function can be obtained by numerical integration of the input data over the available interval at each value of the Fourier conjugate variable (frequency, for example) for which the value of the Fourier transform is desired.[49]
Explicit numerical integration over the ordered pairs can yield the Fourier transform output value for any desired value of the conjugate Fourier transform variable (frequency, for example), so that a spectrum can be produced at any desired step size and over any desired variable range for accurate determination of amplitudes, frequencies, and phases corresponding to isolated peaks. Unlike limitations in DFT and FFT methods, explicit numerical integration can have any desired step size and compute the Fourier transform over any desired range of the conjugate Fourier transform variable (for example, frequency).
Furye diskret va tezkor Furye konvertatsiyalari
If the ordered pairs representing the original input function are equally spaced in their input variable (for example, equal time steps), then the Fourier transform is known as a diskret Furye konvertatsiyasi (DFT), which can be computed either by explicit numerical integration, by explicit evaluation of the DFT definition, or by tez Fourier konvertatsiyasi (FFT) methods. In contrast to explicit integration of input data, use of the DFT and FFT methods produces Fourier transforms described by ordered pairs of step size equal to the reciprocal of the original sampling interval. For example, if the input data is sampled every 10 seconds, the output of DFT and FFT methods will have a 0.1 Hz frequency spacing.
Muhim Furye konvertatsiyasining jadvallari
The following tables record some closed-form Fourier transforms. Funktsiyalar uchun f (x), g(x) va h(x) denote their Fourier transforms by f̂, ĝva ĥ navbati bilan. Only the three most common conventions are included. It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.
Funktsional munosabatlar, bir o'lchovli
The Fourier transforms in this table may be found in Erdélyi (1954) yoki Kammler (2000, appendix).
| Funktsiya | Furye konvertatsiyasi unitary, ordinary frequency | Furye konvertatsiyasi unitary, angular frequency | Furye konvertatsiyasi non-unitary, angular frequency | Izohlar | |
|---|---|---|---|---|---|
| Ta'rif | |||||
| 101 | Lineerlik | ||||
| 102 | Shift in time domain | ||||
| 103 | Shift in frequency domain, dual of 102 | ||||
| 104 | Scaling in the time domain. Agar |a| is large, then f (bolta) is concentrated around 0 and spreads out and flattens. | ||||
| 105 | Duality. Bu yerda f̂ needs to be calculated using the same method as Fourier transform column. Results from swapping "dummy" variables of x va ξ yoki ω yoki ν. | ||||
| 106 | |||||
| 107 | This is the dual of 106 | ||||
| 108 | Notation f ∗ g belgisini bildiradi konversiya ning f va g — this rule is the konvulsiya teoremasi | ||||
| 109 | This is the dual of 108 | ||||
| 110 | Uchun f (x) purely real | Hermitian symmetry. z ni bildiradi murakkab konjugat. | |||
| 111 | Uchun f (x) purely real and hatto | f̂ (ξ), f̂ (ω) va f̂ (ν) are purely real even functions. | |||
| 112 | Uchun f (x) purely real and g'alati | f̂ (ξ), f̂ (ω) va f̂ (ν) are purely xayoliy odd functions. | |||
| 113 | Uchun f (x) purely imaginary | z ni bildiradi murakkab konjugat. | |||
| 114 | Murakkab konjugatsiya, generalization of 110 and 113 | ||||
| 115 | This follows from rules 101 and 103 using Eyler formulasi: | ||||
| 116 | This follows from 101 and 103 using Eyler formulasi: | ||||
Kvadrat bilan birlashtiriladigan funktsiyalar, bir o'lchovli
The Fourier transforms in this table may be found in Campbell & Foster (1948), Erdélyi (1954), yoki Kammler (2000, appendix).
| Funktsiya | Furye konvertatsiyasi unitary, ordinary frequency | Furye konvertatsiyasi unitary, angular frequency | Furye konvertatsiyasi non-unitary, angular frequency | Izohlar | |
|---|---|---|---|---|---|
| 201 | The rectangular pulse va normallashtirilgan sinc funktsiyasi, here defined as sinc(x) = gunoh (πx)/πx | ||||
| 202 | Dual of rule 201. The to'rtburchaklar funktsiya is an ideal past o'tkazgichli filtr, va sinc funktsiyasi bo'ladi sababsiz impulse response of such a filter. The sinc funktsiyasi is defined here as sinc(x) = gunoh (πx)/πx | ||||
| 203 | Funktsiya tri(x) bo'ladi triangular function | ||||
| 204 | Dual of rule 203. | ||||
| 205 | Funktsiya siz(x) bo'ladi Heaviside unit step function va a > 0. | ||||
| 206 | This shows that, for the unitary Fourier transforms, the Gauss funktsiyasi e−ax2 is its own Fourier transform for some choice of a. For this to be integrable we must have Re(a) > 0. | ||||
| 207 | This is known as the complex quadratic-phase sinusoid, or the "chirp" function.[50] | ||||
| 208 | Uchun Re(a) > 0. That is, the Fourier transform of a two-sided decaying exponential function a Lorentzian function. | ||||
| 209 | Giperbolik sekant is its own Fourier transform | ||||
| 210 | Hn bo'ladi nth-order Hermit polinom. Agar a = 1 then the Gauss–Hermite functions are o'ziga xos funktsiyalar of the Fourier transform operator. For a derivation, see Hermit polinom. The formula reduces to 206 for n = 0. |
Tarqatish, bir o'lchovli
The Fourier transforms in this table may be found in Erdélyi (1954) yoki Kammler (2000, appendix).
| Funktsiya | Furye konvertatsiyasi unitary, ordinary frequency | Furye konvertatsiyasi unitary, angular frequency | Furye konvertatsiyasi non-unitary, angular frequency | Izohlar | |
|---|---|---|---|---|---|
| 301 | Tarqatish δ(ξ) belgisini bildiradi Dirac delta funktsiyasi. | ||||
| 302 | 301-qoida. | ||||
| 303 | Bu 103 va 301 raqamlaridan kelib chiqadi. | ||||
| 304 | Bu 101 va 303 qoidalaridan foydalanish Eyler formulasi: | ||||
| 305 | Bu 101 va 303 dan foydalanib keladi | ||||
| 306 | Bu 101 va 207 dan foydalanib keladi | ||||
| 307 | Bu 101 va 207 dan foydalanib keladi | ||||
| 308 | Bu yerda, n a tabiiy son va δ(n)(ξ) bo'ladi nDirac delta funktsiyasining tarqatish hosilasi. Ushbu qoida 107 va 301 qoidalaridan kelib chiqadi. Ushbu qoidani 101 bilan birlashtirib, barchasini o'zgartira olamiz polinomlar. | ||||
| 308-qoida. δ(n)(ξ) bo'ladi nDirac delta funktsiyasining tarqatish hosilasi. Ushbu qoida 106 va 302 dan kelib chiqadi. | |||||
| 309 | Bu yerda sgn (ξ) bo'ladi belgi funktsiyasi. Yozib oling 1/x tarqatish emas. Dan foydalanish kerak Koshining asosiy qiymati qarshi sinov paytida Shvarts vazifalari. Ushbu qoida Hilbert o'zgarishi. | ||||
| 310 | 1/xn bo'ladi bir hil taqsimot tarqatish hosilasi bilan aniqlangan | ||||
| 311 | Ushbu formula uchun amal qiladi 0 > a > −1. Uchun a > 0 ba'zi bir alohida atamalar kelib chiqish joyida paydo bo'ladi, ularni farqlash orqali topish mumkin 318. Agar Qayta a > −1, keyin |x|a mahalliy darajada integral funktsiya va shuning uchun temperli taqsimot. Funktsiya a ↦ |x|a - o'ng yarim tekislikdan tortib taqsimlanishlar fazosigacha bo'lgan holomorf funktsiya. U temperaturali taqsimotga noyob meromorfik kengaytmani ham belgilaydi |x|a uchun a ≠ −2, −4,... (Qarang bir hil taqsimot.) | ||||
| Maxsus ish 311. | |||||
| 312 | 309-qoidaning duali. Bu safar Furye konvertatsiyasini a deb hisoblash kerak Koshining asosiy qiymati. | ||||
| 313 | Funktsiya siz(x) Heaviside birlik qadam funktsiyasi; bu 101, 301 va 312 qoidalaridan kelib chiqadi. | ||||
| 314 | Ushbu funktsiya sifatida tanilgan Dirak tarağı funktsiya. Ushbu natija 302 va 102 dan olinishi mumkin, shu bilan birga tarqatish sifatida. | ||||
| 315 | Funktsiya J0(x) nolinchi tartib Bessel funktsiyasi birinchi turdagi. | ||||
| 316 | Bu 315. umumlashtirish. Funktsiya Jn(x) bo'ladi nbuyurtma Bessel funktsiyasi birinchi turdagi. Funktsiya Tn(x) bo'ladi Chebyshev birinchi turdagi polinom. | ||||
| 317 | γ bo'ladi Eyler-Maskeroni doimiysi. | ||||
| 318 | Ushbu formula uchun amal qiladi 1 > a > 0. Yuqori darajadagi ko'rsatkichlar uchun formulani olish uchun differentsiatsiyadan foydalaning. siz Heaviside funktsiyasi. |
Ikki o'lchovli funktsiyalar
| Funktsiya | Furye konvertatsiyasi unitar, oddiy chastota | Furye konvertatsiyasi unitar, burchak chastotasi | Furye konvertatsiyasi unitar bo'lmagan, burchak chastotasi | Izohlar | |
|---|---|---|---|---|---|
| 400 | O'zgaruvchilar ξx, ξy, ωx, ωy, νx, νy haqiqiy sonlar. Integrallar butun tekislik bo'yicha olinadi. | ||||
| 401 | Ikkala funktsiya ham birlik hajmiga ega bo'lmasligi mumkin bo'lgan Gausslardir. | ||||
| 402 | Funktsiya tomonidan belgilanadi tsirk (r) = 1 uchun 0 ≤ r ≤ 1, aks holda 0 ga teng. Natijada amplituda taqsimlanadi Havodor disk, va yordamida ifodalanadi J1 (buyurtma-1 Bessel funktsiyasi birinchi turdagi).[51] | ||||
| 403 | Bu Hankel konvertatsiyasi ning r−1, 2-o'lchovli Furye "o'zini o'zgartirishi".[50] | ||||
| 404 |
Umumiy uchun formulalar no'lchovli funktsiyalar
| Funktsiya | Furye konvertatsiyasi unitar, oddiy chastota | Furye konvertatsiyasi unitar, burchak chastotasi | Furye konvertatsiyasi unitar bo'lmagan, burchak chastotasi | Izohlar | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | Funktsiya χ[0, 1] bo'ladi ko'rsatkich funktsiyasi intervalgacha [0, 1]. Funktsiya Γ (x) gamma funktsiyasi. Funktsiya Jn/2 + δ birinchi turdagi Bessel funktsiyasidir, tartib bilan n/2 + δ. Qabul qilish n = 2 va δ = 0 402 ishlab chiqaradi.[52] | ||||
| 502 | Qarang Riesz salohiyati bu erda doimiylik beriladi Formulalar hammasi uchun amal qiladi a ≠ −n, −n − 1, ... analitik davom ettirish bilan, ammo keyinchalik funktsiya va uning Furye konvertatsiyasini mos ravishda tartibga solingan temperaturali taqsimot deb tushunish kerak. Qarang bir hil taqsimot.[6-izoh] | ||||
| 503 | Bu $ a $ uchun formuladir ko'p o'zgaruvchan normal taqsimot o'rtacha 0 ga teng bo'lgan 1 ga normalizatsiya qilingan. Qalin o'zgaruvchilar - bu vektorlar yoki matritsalar. Yuqorida aytib o'tilgan sahifaning yozuvlaridan so'ng, Σ = σ σT va Σ−1 = σ.T σ−1 | ||||
| 504 | Bu yerda[53] Qayta (a) > 0 |
Shuningdek qarang
- Analog signalni qayta ishlash
- Beevers-Lipson strip
- Furye diskret konvertatsiyasi
- Tez Fourier konvertatsiyasi
- Fourier integral operatori
- Furye inversiya teoremasi
- Furye multiplikatori
- Fourier seriyasi
- Furye sinus transformatsiyasi
- Furye-Deligne konvertatsiyasi
- Furye-Mukay konvertatsiyasi
- Kesirli Furye konvertatsiyasi
- Bilvosita Fourier konvertatsiyasi
- Integral konvertatsiya
- Laplasning o'zgarishi
- Chiziqli kanonik konvertatsiya
- Mellin o'zgarishi
- Ko'p o'lchovli konvertatsiya
- NGC 4622, ayniqsa NGC 4622 Fourier tasvirini o'zgartiradi m = 2.
- Lokal bo'lmagan operator
- Kvant Fourier konvertatsiyasi
- Qisqa vaqt ichida Fourier konvertatsiyasi
- Spektral zichlik
- Simvolik integratsiya
- Furye transformatsiyasini vaqtni uzaytirish
- Transformatsiya (matematika)
Izohlar
- ^ Uning kattaligi Furye konvensiyasining ishlatilishiga bog'liq bo'lgan xayoliy doimiy omilgacha.
- ^ Ilovaga qarab a Lebesg integrali, tarqatishyoki boshqa yondashuv eng mos bo'lishi mumkin.
- ^ Vretblad (2000) ushbu rasmiy protseduralar uchun chuqur asosga ega bo'lmagan holda qat'iy asoslarni taqdim etadi funktsional tahlil yoki tarqatish nazariyasi.
- ^ Yilda relyativistik kvant mexanikasi ko'p komponentli to'lqin funktsiyalarining vektor qiymatidagi Fourier konvertatsiyasiga duch keladi. Yilda kvant maydon nazariyasi, kosmos vaqtidagi operator tomonidan baholanadigan funktsiyalarning operator tomonidan baholangan Furye konvertatsiyalari tez-tez ishlatiladi, masalan Greiner va Reinhardt (1996).
- ^ Funktsiya shuningdek, chastotali signaldir , ammo integral ikkalasida ham bir xil javoblarni keltirib chiqaradi va , bu ham mos keladi Eyler formulasi:
- ^ Yilda Gelfand va Shilov 1964 yil, p. 363, ushbu jadvalning unitar bo'lmagan konventsiyalari bilan bo'lish uchun berilgan
undan kelib chiqadigan narsa, bilan .
Izohlar
- ^ Kaiser 1994 yil, p. 29.
- ^ Rahmon 2011 yil, p. 11.
- ^ "Elektromagnit (EM) to'lqinlaridagi konventsiyalar" (PDF).
- ^ Furye 1822 yil, p. 525.
- ^ Furye 1878, p. 408.
- ^ (Iordaniya 1883 yil) 216–226-betlarda isbotlangan Furye integral teoremasi Fourier seriyasini o'rganishdan oldin.
- ^ Titchmarsh 1986 yil, p. 1.
- ^ Rahmon 2011 yil, p. 10.
- ^ Folland 1989 yil.
- ^ Furye 1822 yil.
- ^ Taneja 2008 yil, p. 192.
- ^ a b Stein & Shakarchi 2003 yil.
- ^ a b v d e Pinsky 2002 yil.
- ^ a b v d e Katsnelson 1976 yil.
- ^ a b v d e f Stein & Vayss 1971 yil.
- ^ Rudin 1987 yil, p. 187.
- ^ Rudin 1987 yil, p. 186.
- ^ a b Duoandikoetxea 2001 yil.
- ^ a b Boashash 2003 yil.
- ^ Kondon 1937 yil.
- ^ Xau 1980 yil.
- ^ Paley va Wiener 1934 yil.
- ^ Gelfand va Vilenkin 1964 yil.
- ^ Kirillov va Gvishiani 1982 yil.
- ^ Clozel & Delorme 1985 yil, 331–333-betlar.
- ^ de Groot & Mazur 1984 yil, p. 146.
- ^ Champeni 1987 yil, p. 80.
- ^ a b v Kolmogorov va Fomin 1999 yil.
- ^ Wiener 1949 yil.
- ^ Champeni 1987 yil, p. 63.
- ^ Widder & Wiener 1938 yil, p. 537.
- ^ Pinsky 2002 yil, p. 131.
- ^ Stein & Shakarchi 2003 yil, p. 158.
- ^ Chatfild 2004 yil, p. 113.
- ^ Furye 1822 yil, p. 441.
- ^ Puankare 1895 yil, p. 102.
- ^ Whittaker va Watson 1927 yil, p. 188.
- ^ Grafakos 2004 yil.
- ^ Grafakos va Teschl 2013.
- ^ "Amaliy Furye tahlili va zamonaviy signallarni qayta ishlash elementlari 3-ma'ruza". (PDF). 2016 yil 12-yanvar. Olingan 2019-10-11.
- ^ Stein & Vayss 1971 yil, Thm. 2.3.
- ^ Pinsky 2002 yil, p. 256.
- ^ Hewitt & Ross 1970 yil, 8-bob.
- ^ Knapp 2001 yil.
- ^ Gradshteyn va boshq. 2015 yil.
- ^ Press et al. 1992 yil.
- ^ Beyli va Swarztrauber 1994 yil.
- ^ Lado 1971 yil.
- ^ Simonen va Olkkonen 1985 yil.
- ^ a b Jr, Rojer L. Easton (2010). Tasvirlashda Fourier usullari. John Wiley & Sons. ISBN 978-0-470-68983-7. Olingan 26 may 2020.
- ^ Stein & Vayss 1971 yil, Thm. IV.3.3.
- ^ Stein & Vayss 1971 yil, Thm. 4.15.
- ^ Stein & Vayss 1971 yil, p. 6.
Adabiyotlar
- Beyli, Devid X.; Swarztrauber, Pol N. (1994), "Furye va Laplasning doimiy o'zgarishini sonli baholashning tezkor usuli" (PDF), Ilmiy hisoblash bo'yicha SIAM jurnali, 15 (5): 1105–1110, CiteSeerX 10.1.1.127.1534, doi:10.1137/0915067.
- Boashash, B., ed. (2003), Vaqt chastotasi signallarini tahlil qilish va qayta ishlash: keng qamrovli ma'lumot, Oksford: Elsevier Science, ISBN 978-0-08-044335-5.
- Bochner, S.; Chandrasekharan, K. (1949), Furye o'zgarishi, Prinston universiteti matbuoti.
- Bracewell, R. N. (2000), Furye transformatsiyasi va uning qo'llanilishi (3-nashr), Boston: McGraw-Hill, ISBN 978-0-07-116043-8.
- Kempbell, Jorj; Foster, Ronald (1948), Amaliy qo'llanmalar uchun Fourier integrallari, Nyu-York: D. Van Nostrand kompaniyasi, Inc..
- Champeni, DC (1987), Furye teoremalari haqida qo'llanma, Kembrij universiteti matbuoti.
- Chatfild, Kris (2004), Vaqt seriyasining tahlili: Kirish, Statistika fanidagi matnlar (6-nashr), London: Chapman & Hall / CRC, ISBN 9780203491683.
- Klozel, Loran; Delorme, Patris (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs reels", Comptes Rendus de l'Académie des Sciences, Série I, 300: 331–333.
- Kondon, E. U. (1937), "Fursat transformatsiyasining doimiy funktsional transformatsiyalar guruhiga botirilishi", Proc. Natl. Akad. Ilmiy ish., 23 (3): 158–164, Bibcode:1937 yil PNAS ... 23..158C, doi:10.1073 / pnas.23.3.158, PMC 1076889, PMID 16588141.
- de Groot, Sybren R.; Mazur, Piter (1984), Muvozanatsiz termodinamika (2-nashr), Nyu-York: Dover.
- Duoandikoetxea, Xaver (2001), Furye tahlili, Amerika matematik jamiyati, ISBN 978-0-8218-2172-5.
- Dym, H.; McKan, H. (1985), Furye seriyalari va integrallari, Akademik matbuot, ISBN 978-0-12-226451-1.
- Erdélii, Artur, ed. (1954), Integral transformatsiyalar jadvallari, 1, McGraw-Hill.
- Feller, Uilyam (1971), Ehtimollar nazariyasiga kirish va uning qo'llanilishi, II (2-nashr), Nyu-York: Vili, JANOB 0270403.
- Folland, Jerald (1989), Faza fazosidagi harmonik tahlil, Prinston universiteti matbuoti.
- Fourier, JB Jozef (1822), Théorie analytique de la chaleur (frantsuz tilida), Parij: Firmin Didot, père et fils, OCLC 2688081.
- Fourier, JB Jozef (1878) [1822], Issiqlikning analitik nazariyasi, Aleksandr Freeman tomonidan tarjima qilingan, Universitet matbuoti (frantsuz tilidan tarjima qilingan).
- Gradshteyn, Izrail Sulaymonovich; Rijik, Iosif Moiseevich; Geronimus, Yuriy Veniaminovich; Tseytlin, Mixail Yulyevich; Jeffri, Alan (2015), Tsvillinger, Daniel; Moll, Viktor Gyugo (tahr.), Integrallar, seriyalar va mahsulotlar jadvali, Scripta Technica, Inc. tomonidan tarjima qilingan (8-nashr), Akademik matbuot, ISBN 978-0-12-384933-5.
- Grafakos, Loukas (2004), Klassik va zamonaviy Furye tahlili, Prentice-Hall, ISBN 978-0-13-035399-3.
- Grafakos, Loukas; Teschl, Jerald (2013), "Radial funktsiyalar va taqsimotlarning Furye konversiyalari to'g'risida", J. Furye Anal. Qo'llash., 19: 167–179, arXiv:1112.5469, doi:10.1007 / s00041-012-9242-5, S2CID 1280745.
- Greiner, V.; Reinhardt, J. (1996), Maydonlarni kvantlash, Springer, ISBN 978-3-540-59179-5.
- Gelfand, I.M.; Shilov, G.E. (1964), Umumlashtirilgan funktsiyalar, 1, Nyu York: Akademik matbuot (rus tilidan tarjima qilingan).
- Gelfand, I.M.; Vilenkin, N.Y. (1964), Umumlashtirilgan funktsiyalar, 4, Nyu York: Akademik matbuot (rus tilidan tarjima qilingan).
- Xevitt, Edvin; Ross, Kennet A. (1970), Abstrakt harmonik tahlil, Die Grundlehren derhematischen Wissenschaften, 152-band, jild. II: ixcham guruhlar uchun tuzilish va tahlil. Mahalliy ixcham abeliy guruhlari bo'yicha tahlil, Springer, JANOB 0262773.
- Xormander, L. (1976), Lineer qisman differentsial operatorlar, Jild 1, Springer, ISBN 978-3-540-00662-6.
- Xou, Rojer (1980), "Geyzenberg guruhining garmonik tahlildagi roli to'g'risida", Amerika Matematik Jamiyati Axborotnomasi, 3 (2): 821–844, doi:10.1090 / S0273-0979-1980-14825-9, JANOB 0578375.
- Jeyms, JF (2011), Furye transformatsiyalari bo'yicha talabalar uchun qo'llanma (3-nashr), Kembrij universiteti matbuoti, ISBN 978-0-521-17683-5.
- Iordaniya, Kamil (1883), D'Analyse de l'École politexnika, Jild II, Calcul Intégral: Intégrales définies et indéfinies (2-nashr), Parij.
- Kaiser, Jerald (1994), "Wavelets uchun do'stona qo'llanma", Bugungi kunda fizika, 48 (7): 57–58, Bibcode:1995PhT .... 48g..57K, doi:10.1063/1.2808105, ISBN 978-0-8176-3711-8.
- Kammler, Devid (2000), Furye tahlilining birinchi kursi, Prentice Hall, ISBN 978-0-13-578782-3.
- Katznelson, Yitsak (1976), Harmonik tahlilga kirish, Dover, ISBN 978-0-486-63331-2.
- Kirillov, Aleksandr; Gvishiani, Aleksey D. (1982) [1979], Funktsional tahlildagi teoremalar va muammolar, Springer (rus tilidan tarjima qilingan).
- Knapp, Entoni V. (2001), Semisimple guruhlarining vakillik nazariyasi: misollarga asoslangan umumiy nuqtai, Prinston universiteti matbuoti, ISBN 978-0-691-09089-4.
- Kolmogorov, Andrey Nikolaevich; Fomin, Sergey Vasilevich (1999) [1957], Funksiyalar va funktsional tahlil nazariyasining elementlari, Dover (rus tilidan tarjima qilingan).
- Lado, F. (1971), "Suyuq holatni hisoblash uchun raqamli Furye bir, ikki va uch o'lchovli transformatsiyalar", Hisoblash fizikasi jurnali, 8 (3): 417–433, Bibcode:1971JCoPh ... 8..417L, doi:10.1016/0021-9991(71)90021-0.
- Myuller, Meinard (2015), Qisqa qilib aytganda Furye o'zgarishi. (PDF), In Musiqani qayta ishlash asoslari, 2.1 bo'lim, 40-56 betlar: Springer, doi:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, S2CID 8691186CS1 tarmog'i: joylashuvi (havola).
- Paley, R.E.A.C.; Viner, Norbert (1934), Murakkab domendagi Fourier transformatsiyalari, Amerika Matematik Jamiyati Kollokvium nashrlari, Providens, Rod-Aylend: Amerika matematik jamiyati.
- Pinsky, Mark (2002), Fourier Analysis va Wavelets-ga kirish, Bruks / Koul, ISBN 978-0-534-37660-4.
- Puankare, Anri (1895), Théorie analytique de la propagation de la chaleur, Parij: Carré.
- Polyanin, A. D .; Manjirov, A. V. (1998), Integral tenglamalar bo'yicha qo'llanma, Boka Raton: CRC Press, ISBN 978-0-8493-2876-3.
- Matbuot, Uilyam H.; Flannery, Brian P.; Teukolskiy, Shoul A.; Vetterling, Uilyam T. (1992), C-dagi raqamli retseptlar: Ilmiy hisoblash san'ati, ikkinchi nashr (2-nashr), Kembrij universiteti matbuoti.
- Raxman, Matiur (2011), Furye umumiy funktsiyalarga o'tkazilishining qo'llanilishi, WIT Press, ISBN 978-1-84564-564-9.
- Rudin, Valter (1987), Haqiqiy va kompleks tahlil (3-nashr), Singapur: McGraw Hill, ISBN 978-0-07-100276-9.
- Simonen, P .; Olkkonen, H. (1985), "Simpson sonli integrali orqali Furye integralini hisoblashning tezkor usuli", Biomedikal muhandislik jurnali, 7 (4): 337–340, doi:10.1016/0141-5425(85)90067-6, PMID 4057997.
- Shteyn, Elias; Shakarchi, Rami (2003), Furye tahlili: kirish, Prinston universiteti matbuoti, ISBN 978-0-691-11384-5.
- Shteyn, Elias; Vayss, Gvido (1971), Evklid fazosidagi Fourier tahliliga kirish, Prinston, NJ: Prinston universiteti matbuoti, ISBN 978-0-691-08078-9.
- Taneja, XC (2008), "18-bob: Furye integrallari va Furye konvertatsiyalari", Ilg'or muhandislik matematikasi, Jild 2, Nyu-Dehli, Hindiston: I. K. International Pvt Ltd, ISBN 978-8189866563.
- Titchmarsh, E. (1986) [1948], Furye integrallari nazariyasiga kirish (2-nashr), Oksford universiteti: Clarendon Press, ISBN 978-0-8284-0324-5.
- Vretblad, Anders (2000), Furye tahlili va uning qo'llanilishi, Matematikadan aspirantura matnlari, 223, Nyu York: Springer, ISBN 978-0-387-00836-3.
- Uittaker, E. T.; Vatson, G. N. (1927), Zamonaviy tahlil kursi (4-nashr), Kembrij universiteti matbuoti.
- Vidder, Devid Vernon; Viner, Norbert (1938 yil avgust), "Laplas integrali uchun klassik inversiya formulasi haqida eslatmalar", Amerika Matematik Jamiyati Axborotnomasi, 44 (8): 573–575, doi:10.1090 / s0002-9904-1938-06812-7.
- Viner, Norbert (1949), Ekstrapolyatsiya, interpolatsiya va statsionar vaqt turkumlarini muhandislik dasturlari bilan tekislash, Kembrij, Mass.: Technology Press va John Wiley & Sons va Chapman & Hall.
- Uilson, R. G. (1995), Zamonaviy optikada Fourier seriyali va optik transformatsiya usullari, Nyu York: Vili, ISBN 978-0-471-30357-2.
- Yosida, K. (1968), Funktsional tahlil, Springer, ISBN 978-3-540-58654-8.

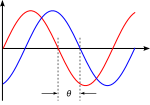
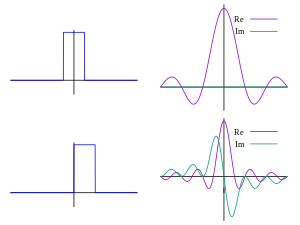






















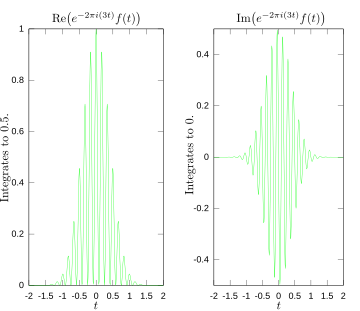
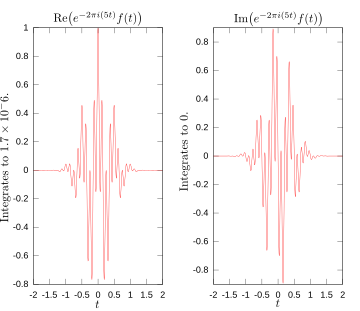
































![{ displaystyle psi _ {n} (x) = { frac { sqrt [{4}] {2}} { sqrt {n!}}} e ^ {- pi x ^ {2}} mathrm {He} _ {n} chap (2x { sqrt { pi}} o'ng),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)




































































































































































































































































































































![{ displaystyle chi _ {[0,1]} (| mathbf {x} |) chap (1- | mathbf {x} | ^ {2} o'ng) ^ { delta}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)























