WikiDer > Hurwitz zeta funktsiyasi - Vikipediya

Yilda matematika, Hurwitz zeta funktsiyasinomi bilan nomlangan Adolf Xurvits, ko'pchiligidan biri zeta funktsiyalari. Bu uchun rasmiy ravishda belgilangan murakkab dalillar s bilan Re (s)> 1 va q bilan Re (q)> 0 tomonidan

${ displaystyle zeta (s, q) = sum _ {n = 0} ^ { infty} { frac {1} {(n + q) ^ {s}}}.}$

Ushbu seriya mutlaqo yaqinlashuvchi ning berilgan qiymatlari uchun s va q va a ga kengaytirilishi mumkin meromorfik funktsiya hamma uchun belgilangan s≠ 1. The Riemann zeta funktsiyasi bu ζ (s,1).

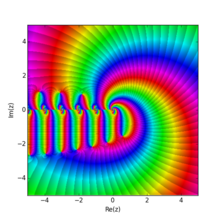
Hurwitz zeta funktsiyasi mos keladi q = 1/3. U sifatida hosil bo'ladi Matplotlib versiyasidan foydalangan holda fitna Domenni bo'yash usul.^[1]

Analitik davomi

Hurwitz zeta funktsiyasi mos keladi q = 24/25.

Agar ${ displaystyle mathrm {Re} (s) leq 1}$ Hurwitz zeta funktsiyasini tenglama bilan aniqlash mumkin

${ displaystyle zeta (s, q) = Gamma (1-s) { frac {1} {2 pi i}} int _ {C} { frac {z ^ {s-1} e ^ {qz}} {1-e ^ {z}}} dz}$

qaerda kontur ${ displaystyle C}$ manfiy real o'qi atrofidagi aylana. Bu analitik davomini ta'minlaydi ${ displaystyle zeta (s, q)}$.

Hurwitz zeta funktsiyasi tomonidan kengaytirilishi mumkin analitik davomi a meromorfik funktsiya barcha murakkab sonlar uchun aniqlangan ${ displaystyle s}$ bilan ${ displaystyle s neq 1}$. Da ${ displaystyle s = 1}$ u bor oddiy qutb bilan qoldiq ${ displaystyle 1}$. Doimiy atama tomonidan berilgan

${ displaystyle lim _ {s to 1} chap [ zeta (s, q) - { frac {1} {s-1}} right] = { frac {- Gamma '(q) } { Gamma (q)}} = - psi (q)}$

qayerda ${ displaystyle Gamma}$ bo'ladi gamma funktsiyasi va ${ displaystyle psi}$ bo'ladi digamma funktsiyasi.

Seriyani namoyish qilish

Hurwitz zeta funktsiyasi sifatida q bilan s = 3+4men.

Konvergent Nyuton seriyasi (haqiqiy) uchun belgilangan vakillik q > 0 va har qanday kompleks s ≠ 1 tomonidan berilgan Helmut Hasse 1930 yilda:^[2]

${ displaystyle zeta (s, q) = { frac {1} {s-1}} sum _ {n = 0} ^ { infty} { frac {1} {n + 1}} sum _ {k = 0} ^ {n} (- 1) ^ {k} {n k} (q + k) ^ {1-s} ni tanlang.}$

Ushbu ketma-ketlik bir xilda yaqinlashadi ixcham pastki to'plamlar ning s- samolyot butun funktsiya. Ichki summani quyidagicha tushunish mumkin nth oldinga farq ning ${ displaystyle q ^ {1-s}}$; anavi,

${ displaystyle Delta ^ {n} q ^ {1-s} = sum _ {k = 0} ^ {n} (- 1) ^ {nk} {n k} (q + k) ^ {ni tanlang 1-s}}$

bu erda Δ oldinga farq operatori. Shunday qilib, kimdir yozishi mumkin

${ displaystyle { begin {aligned} zeta (s, q) & = { frac {1} {s-1}} sum _ {n = 0} ^ { infty} { frac {(-1 ) ^ {n}} {n + 1}} Delta ^ {n} q ^ {1-s} & = { frac {1} {s-1}} { log (1+ Delta) over Delta} q ^ {1-s} end {aligned}}}$

Global miqyosda yaqinlashayotgan boshqa qatorlarga ushbu misollar kiradi

${ displaystyle zeta (s, v-1) = { frac {1} {s-1}} sum _ {n = 0} ^ { infty} H_ {n + 1} sum _ {k = 0} ^ {n} (- 1) ^ {k} { binom {n} {k}} (k + v) ^ {1-s}}$

${ displaystyle zeta (s, v) = { frac {k!} {(sk) _ {k}}} sum _ {n = 0} ^ { infty} { frac {1} {(n) + k)!}} chap [{n + k tepada n} o'ng] sum _ {l = 0} ^ {n + k-1} ! (- 1) ^ {l} { binom { n + k-1} {l}} (l + v) ^ {ks}, quad k = 1,2,3, ldots}$

${ displaystyle zeta (s, v) = { frac {v ^ {1-s}} {s-1}} + sum _ {n = 0} ^ { infty} | G_ {n + 1} | sum _ {k = 0} ^ {n} (- 1) ^ {k} { binom {n} {k}} (k + v) ^ {- s}}$

${ displaystyle zeta (s, v) = { frac {(v-1) ^ {1-s}} {s-1}} - sum _ {n = 0} ^ { infty} C_ {n +1} sum _ {k = 0} ^ {n} (- 1) ^ {k} { binom {n} {k}} (k + v) ^ {- s}}$

${ displaystyle zeta (s, v) { big (} v - { tfrac {1} {2}} { big)} = { frac {s-2} {s-1}} zeta ( s-1, v) + sum _ {n = 0} ^ { infty} (- 1) ^ {n} G_ {n + 2} sum _ {k = 0} ^ {n} (- 1) ^ {k} { binom {n} {k}} (k + v) ^ {- s}}$

${ displaystyle zeta (s, v) = - sum _ {l = 1} ^ {k-1} { frac {(k-l + 1) _ {l}} {(sl) _ {l} }} zeta (sl, v) + sum _ {l = 1} ^ {k} { frac {(k-l + 1) _ {l}} {(sl) _ {l}}} v ^ {ls} + k sum _ {n = 0} ^ { infty} (- 1) ^ {n} G_ {n + 1} ^ {(k)} sum _ {k = 0} ^ {n} (-1) ^ {k} { binom {n} {k}} (k + v) ^ {- s}}$

qayerda H_n ular Harmonik raqamlar, ${ displaystyle left [{ cdot atop cdot} right]}$ ular Birinchi turdagi raqamlar, ${ displaystyle ( ldots) _ { ldots}}$ bo'ladi Pochhammer belgisi, G_n ular Gregori koeffitsientlari, G^(k)
_n ular Gregori koeffitsientlari yuqori darajadagi va C_n Ikkinchi turdagi Koshi raqamlari (C₁ = 1/2, C₂ = 5/12, C₃ = 3/8, ...), Blagouchine qog'oziga qarang.^[3]

Integral vakillik

Funktsiyaning nuqtai nazaridan ajralmas vakili mavjud Mellin o'zgarishi kabi

${ displaystyle zeta (s, q) = { frac {1} { Gamma (s)}}} int _ {0} ^ { infty} { frac {t ^ {s-1} e ^ { -qt}} {1-e ^ {- t}}} dt}$

uchun ${ displaystyle Re s> 1}$ va ${ displaystyle Re q> 0.}$

Xurvits formulasi

Xurvits formulasi bu teorema

${ displaystyle zeta (1-s, x) = { frac {1} {2s}} left [e ^ {- i pi s / 2} beta (x; s) + e ^ {i pi s / 2} beta (1-x; s) o'ng]}$

qayerda

${ displaystyle beta (x; s) = 2 Gamma (s + 1) sum _ {n = 1} ^ { infty} { frac { exp (2 pi inx)} {(2 pi) n) ^ {s}}} = { frac {2 Gamma (s + 1)} {(2 pi) ^ {s}}} { mbox {Li}} _ {s} (e ^ {2) pi ix})}$

uchun amal qiladigan zeta vakili ${ displaystyle 0 leq x leq 1}$ va s> 1. Mana, ${ displaystyle { text {Li}} _ {s} (z)}$ bo'ladi polilogarifma.

Funktsional tenglama

The funktsional tenglama murakkab tekislikning chap va o'ng tomonlaridagi zeta qiymatlarini bog'laydi. Butun sonlar uchun ${ displaystyle 1 leq m leq n}$,

${ displaystyle zeta left (1-s, { frac {m} {n}} right) = { frac {2 Gamma (s)} {(2 pi n) ^ {s}}} sum _ {k = 1} ^ {n} chap [ cos chap ({ frac { pi s} {2}} - { frac {2 pi km} {n}} o'ng) ; zeta left (s, { frac {k} {n}} right) right]}$

ning barcha qiymatlari uchun amal qiladi s.

Ba'zi cheklangan summalar

Funktsional tenglama bilan chambarchas bog'liq bo'lgan quyidagi cheklangan yig'indilar mavjud, ularning ba'zilari yopiq shaklda baholanishi mumkin

${ displaystyle sum _ {r = 1} ^ {m-1} zeta left (s, { frac {r} {m}} right) cos { dfrac {2 pi rk} {m }} = { frac {m Gamma (1-s)} {(2 pi m) ^ {1-s}}} sin { frac { pi s} {2}} cdot left { zeta chap (1-s, { frac {k} {m}} o'ng) + zeta chap (1-s, 1 - { frac {k} {m}} o'ng) o'ng } - zeta (lar)}$

${ displaystyle sum _ {r = 1} ^ {m-1} zeta left (s, { frac {r} {m}} right) sin { dfrac {2 pi rk} {m }} = { frac {m Gamma (1-s)} {(2 pi m) ^ {1-s}}} cos { frac { pi s} {2}} cdot left { zeta chap (1-s, { frac {k} {m}} o'ng) - zeta chap (1-s, 1 - { frac {k} {m}} o'ng) o'ng }}$

${ displaystyle sum _ {r = 1} ^ {m-1} zeta ^ {2} left (s, { frac {r} {m}} right) = { big (} m ^ { 2s-1} -1 { big)} zeta ^ {2} (s) + { frac {2m Gamma ^ {2} (1-s)} {(2 pi m) ^ {2-2s }}} sum _ {l = 1} ^ {m-1} left { zeta left (1-s, { frac {l} {m}} right) - cos pi s cdot zeta chap (1-s, 1 - { frac {l} {m}} o'ng) o'ng } zeta chap (1-s, { frac {l} {m}} o'ng )}$

qayerda m 2 dan katta musbat butun son s murakkab, masalan, qarang. B ilova.^[4]

Teylor seriyasi

Ikkinchi argumentda zeta lotin a siljish:

${ displaystyle { frac { qismli} { qisman q}} zeta (s, q) = - s zeta (s + 1, q).}$

Shunday qilib, Teylor seriyasi quyidagicha yozilishi mumkin:

${ displaystyle zeta (s, x + y) = sum _ {k = 0} ^ { infty} { frac {y ^ {k}} {k!}} { frac { qismli ^ {k }} { qisman x ^ {k}}} zeta (s, x) = sum _ {k = 0} ^ { infty} {s + k-1 s-1} (- y) ^ ni tanlang {k} zeta (s + k, x).}$

Shu bilan bir qatorda,

${ displaystyle zeta (s, q) = { frac {1} {q ^ {s}}} + sum _ {n = 0} ^ { infty} (- q) ^ {n} {s + n-1 ni tanlang n} zeta (s + n),}$

bilan ${ displaystyle | q | <1}$.^[5]

Bilan chambarchas bog'liq Shtark-Keyper formula:

${ displaystyle zeta (s, N) = sum _ {k = 0} ^ { infty} left [N + { frac {s-1} {k + 1}} right] {s + k- 1 s-1} (- 1) ^ {k} zeta (s + k, N)} ni tanlang$

tamsayıga teng N va o'zboshimchalik bilan s. Shuningdek qarang Faolxabarning formulasi tamsayılar kuchlarining cheklangan yig'indisiga o'xshash munosabat uchun.

Loran seriyasi

The Loran seriyasi kengaytirishni aniqlash uchun ishlatish mumkin Stieltjes konstantalari ketma-ketlikda uchraydi

${ displaystyle zeta (s, q) = { frac {1} {s-1}} + sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {n!}} gamma _ {n} (q) ; (s-1) ^ {n}.}$

Xususan ${ displaystyle gamma _ {0} (q) = - psi (q)}$ va ${ displaystyle gamma _ {0} (1) = - psi (1) = gamma _ {0} = gamma}$.

Furye konvertatsiyasi

The diskret Furye konvertatsiyasi buyruqqa nisbatan Hurwitz zeta funktsiyasining s bo'ladi Legendre chi funktsiyasi.

Bernulli polinomlariga munosabat

Funktsiya ${ displaystyle beta}$ yuqorida tavsiflangan Bernulli polinomlari:

${ displaystyle B_ {n} (x) = - Re left [(- i) ^ {n} beta (x; n) right]}$

qayerda ${ displaystyle Re z}$ ning haqiqiy qismini bildiradi z. Shu bilan bir qatorda,

${ displaystyle zeta (-n, x) = - {B_ {n + 1} (x) n + 1} dan yuqori.}$

Xususan, munosabat uchun amal qiladi ${ displaystyle n = 0}$ va bittasi bor

${ displaystyle zeta (0, x) = { frac {1} {2}} - x.}$

Yakobi teta funktsiyasi bilan bog'liqlik

Agar ${ displaystyle vartheta (z, tau)}$ bu Jakobi teta funktsiyasi, keyin

${ displaystyle int _ {0} ^ { infty} left [ vartheta (z, it) -1 right] t ^ {s / 2} { frac {dt} {t}} = pi ^ {- (1-s) / 2} Gamma chap ({ frac {1-s} {2}} o'ng) chap [ zeta (1-s, z) + zeta (1-s, 1-z) o'ng]}$

uchun ushlab turadi ${ displaystyle Re s> 0}$ va z murakkab, ammo butun son emas. Uchun z=n butun son, bu soddalashtiradi

${ displaystyle int _ {0} ^ { infty} left [ vartheta (n, it) -1 right] t ^ {s / 2} { frac {dt} {t}} = 2 pi ^ {- (1-s) / 2} Gamma chap ({ frac {1-s} {2}} o'ng) zeta (1-s) = 2 pi ^ {- s / 2} Gamma chap ({ frac {s} {2}} o'ng) zeta (s).}$

qaerda ζ bu erda Riemann zeta funktsiyasi. Ushbu oxirgi shakl funktsional tenglama dastlab Riemann tomonidan berilgan Riemann zeta funktsiyasi uchun. Asosida ajratilgan z tamsayı bo'lish yoki bo'lmaslik Jakobi teta funktsiyasining davriyga yaqinlashishini hisobga oladi delta funktsiyasi, yoki Dirak tarağı yilda z kabi ${ displaystyle t rightarrow 0}$.

Dirichlet bilan munosabat L-funktsiyalar

Ratsional argumentlarda Hurwitz zeta funktsiyasi ning chiziqli birikmasi sifatida ifodalanishi mumkin Dirichlet L-funktsiyalari va aksincha: Hurwitz zeta funktsiyasi bilan mos keladi Riemannning zeta funktsiyasi ζ (s) qachon q = 1, qachon q = 1/2 ga teng (2^s−1) ζ (s),^[6] va agar q = n/k bilan k > 2, (n,k)> 1 va 0 <n < k, keyin^[7]

${ displaystyle zeta (s, n / k) = { frac {k ^ {s}} { varphi (k)}} sum _ { chi} { overline { chi}} (n) L (s, chi),}$

yig'indisi hammasi ustida ishlaydi Dirichlet belgilar mod k. Qarama-qarshi yo'nalishda biz chiziqli kombinatsiyaga egamiz^[6]

${ displaystyle L (s, chi) = { frac {1} {k ^ {s}}} sum _ {n = 1} ^ {k} chi (n) ; zeta left (s) , { frac {n} {k}} o'ng).}$

Shuningdek, mavjud ko'paytirish teoremasi

${ displaystyle k ^ {s} zeta (s) = sum _ {n = 1} ^ {k} zeta left (s, { frac {n} {k}} right),}$

shundan foydali umumlashma tarqatish munosabati^[8]

${ displaystyle sum _ {p = 0} ^ {q-1} zeta (s, a + p / q) = q ^ {s} , zeta (s, qa).}$

(Ushbu oxirgi shakl har doim amal qiladi q tabiiy raqam va 1 -qa emas.)

Nol

Agar q= 1 Hurwitz zeta funktsiyasi kamayadi Riemann zeta funktsiyasi o'zi; agar q= 1/2 u murakkab argumentning oddiy funktsiyasiga ko'paytiriladigan Riemann zeta funktsiyasini kamaytiradi s (vide supra), har holda Rimannning zeta funktsiyasining nollarini qiyin o'rganishga olib keladi. Xususan, haqiqiy qismi 1 dan katta yoki unga teng nollar bo'lmaydi. Ammo, agar 0 q<1 va q≠ 1/2, keyin 1 tasmada Xurvitsning zeta funktsiyasining nollari mavjud s) Har qanday ijobiy real haqiqiy son uchun <1 +. Bu isbotlangan Davenport va Xeylbronn oqilona yoki transandantal irratsional uchun q,^[9] va tomonidan Kasselalar algebraik irratsional uchun q.^[6][10]

Ratsional qadriyatlar

Hurwitz zeta funktsiyasi ratsional qiymatlarda bir qator ajoyib o'ziga xosliklarda uchraydi.^[11] Xususan, Eyler polinomlari ${ displaystyle E_ {n} (x)}$:

${ displaystyle E_ {2n-1} left ({ frac {p} {q}} right) = (- 1) ^ {n} { frac {4 (2n-1)!} {(2 ) pi q) ^ {2n}}} sum _ {k = 1} ^ {q} zeta chap (2n, { frac {2k-1} {2q}} o'ng) cos { frac {( 2k-1) pi p} {q}}}$

va

${ displaystyle E_ {2n} chap ({ frac {p} {q}} o'ng) = (- 1) ^ {n} { frac {4 (2n)!} {(2 pi q) ^ {2n + 1}}} sum _ {k = 1} ^ {q} zeta chap (2n + 1, { frac {2k-1} {2q}} o'ng) sin { frac {( 2k-1) pi p} {q}}}$

Bittasi ham bor

${ displaystyle zeta left (s, { frac {2p-1} {2q}} right) = 2 (2q) ^ {s-1} sum _ {k = 1} ^ {q} left [C_ {s} chap ({ frac {k} {q}} o'ng) cos chap ({ frac {(2p-1) pi k} {q}} o'ng) + S_ {s } chap ({ frac {k} {q}} o'ng) sin chap ({ frac {(2p-1) pi k} {q}} o'ng) o'ng]}$

uchun ushlab turadigan ${ displaystyle 1 leq p leq q}$. Mana ${ displaystyle C _ { nu} (x)}$ va ${ displaystyle S _ { nu} (x)}$ yordamida aniqlanadi Legendre chi funktsiyasi ${ displaystyle chi _ { nu}}$ kabi

${ displaystyle C _ { nu} (x) = operatorname {Re} , chi _ { nu} (e ^ {ix})}$

va

${ displaystyle S _ { nu} (x) = operator nomi {Im} , chi _ { nu} (e ^ {ix}).}$

Ν ning tamsayı qiymatlari uchun ular Eyler polinomlari ko'rinishida ifodalanishi mumkin. Ushbu munosabatlar yuqorida keltirilgan Xurvits formulasi bilan birgalikda funktsional tenglamani qo'llash orqali olinishi mumkin.

Ilovalar

Xurvitsning zeta funktsiyasi turli fanlarda uchraydi. Odatda, bu sodir bo'ladi sonlar nazariyasi, bu erda uning nazariyasi eng chuqur va eng rivojlangan. Biroq, bu ham o'rganishda uchraydi fraktallar va dinamik tizimlar. Qo'llaniladi statistika, bu sodir bo'ladi Zipf qonuni va Zipf-Mandelbrot qonuni. Yilda zarralar fizikasi, bu formulada uchraydi Julian Shvinger,^[12] uchun aniq natijani berish juft ishlab chiqarish a darajasi Dirak elektron bir xil elektr maydonida.

Maxsus holatlar va umumlashmalar

Hurwitz zeta funktsiyasi musbat tamsayı bilan m bilan bog'liq poligamma funktsiyasi:

${ displaystyle psi ^ {(m)} (z) = (- 1) ^ {m + 1} m! zeta (m + 1, z) .}$

Salbiy tamsayı uchun -n qiymatlari bilan bog'liq Bernulli polinomlari:^[13]

${ displaystyle zeta (-n, x) = - { frac {B_ {n + 1} (x)} {n + 1}} .}$

The Barnes zeta funktsiyasi Hurwitz zeta funktsiyasini umumlashtiradi.

The Lerch transsendent Hurwitz zetasini umumlashtiradi:

${ displaystyle Phi (z, s, q) = sum _ {k = 0} ^ { infty} { frac {z ^ {k}} {(k + q) ^ {s}}}}$

va shunday qilib

${ displaystyle zeta (s, q) = Phi (1, s, q). ,}$

Gipergeometrik funktsiya

${ displaystyle zeta (s, a) = a ^ {- s} cdot {} _ {s + 1} F_ {s} (1, a_ {1}, a_ {2}, ldots a_ {s} ; a_ {1} + 1, a_ {2} +1, ldots a_ {s} +1; 1)}$ qayerda ${ displaystyle a_ {1} = a_ {2} = ldots = a_ {s} = a { text {and}} a notin mathbb {N} { text {and}} s in mathbb { N} ^ {+}.}$

Meijer G-funktsiyasi

${ displaystyle zeta (s, a) = G , _ {s + 1, , s + 1} ^ {, 1, , s + 1} left (-1 ; left | ; { begin {matrix} 0,1-a, ldots, 1-a 0, -a, ldots, -a end {matrix}} right) right. qquad qquad s in mathbb {N} ^ {+}.}$

Izohlar

Adabiyotlar

• Apostol, T. M. (2010), "Hurwitz zeta funktsiyasi", yilda Olver, Frank V. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Klark, Charlz V. (tahr.), NIST Matematik funktsiyalar bo'yicha qo'llanma, Kembrij universiteti matbuoti, ISBN 978-0-521-19225-5, JANOB 2723248
• 12-bobga qarang Apostol, Tom M. (1976), Analitik sonlar nazariyasiga kirish, Matematikadagi bakalavr matnlari, Nyu-York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, JANOB 0434929, Zbl 0335.10001
• Milton Abramovits va Irene A. Stegun, Matematik funktsiyalar bo'yicha qo'llanma, (1964) Dover Publications, Nyu-York. ISBN 0-486-61272-4. (Qarang 6.4.10-band poligamma funktsiyasi bilan bog'liqligi uchun.)
• Davenport, Garold (1967). Multiplikatsion sonlar nazariyasi. Ilg'or matematikadan ma'ruzalar. 1. Chikago: Markxem. Zbl 0159.06303.
• Miller, Jef; Adamchik, Viktor S. (1998). "Hurwitz Zeta funktsiyasining hosilalari mantiqiy dalillar uchun". Hisoblash va amaliy matematika jurnali. 100 (2): 201–206. doi:10.1016 / S0377-0427 (98) 00193-9.
• Vepstas, Linas. "Bernulli operatori, Gauss-Kuzmin-Wirsing operatori va Riemann Zeta" (PDF).
• Mezo, Istvan; Dil, Ayxan (2010). "Hurwitz zeta funktsiyasini o'z ichiga olgan giperharmonik serial". Raqamlar nazariyasi jurnali. 130 (2): 360–369. doi:10.1016 / j.jnt.2009.08.005. hdl:2437/90539.

Tashqi havolalar

• Jonathan Sondow va Erik W. Weisstein. "Hurwitz Zeta funktsiyasi". MathWorld.