Ushbu maqola umumiy Pareto taqsimoti deb ataladigan uzluksiz tarqatishning ma'lum bir oilasi haqida. Umumlashtirilgan Pareto tarqatish ierarxiyasi uchun qarang
Pareto tarqatish .
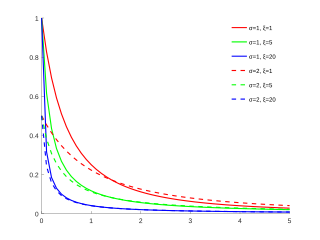
Paretoning umumiy tarqatilishi Ehtimollar zichligi funktsiyasi
Uchun GPD tarqatish funktsiyalari
m = 0 { displaystyle mu = 0} va ning turli xil qiymatlari
σ { displaystyle sigma} va
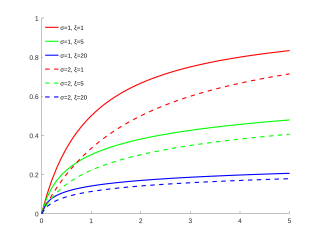
ξ { displaystyle xi} Kümülatif taqsimlash funktsiyasi
Parametrlar m ∈ ( − ∞ , ∞ ) { displaystyle mu in (- infty, infty) ,} Manzil (haqiqiy ) σ ∈ ( 0 , ∞ ) { displaystyle sigma in (0, infty) ,} o'lchov (haqiqiy)
ξ ∈ ( − ∞ , ∞ ) { displaystyle xi in (- infty, infty) ,} shakli (haqiqiy)Qo'llab-quvvatlash x ⩾ m ( ξ ⩾ 0 ) { displaystyle x geqslant mu , ; ( xi geqslant 0)}
m ⩽ x ⩽ m − σ / ξ ( ξ < 0 ) { displaystyle mu leqslant x leqslant mu - sigma / xi , ; ( xi <0)} PDF 1 σ ( 1 + ξ z ) − ( 1 / ξ + 1 ) { displaystyle { frac {1} { sigma}} (1+ xi z) ^ {- (1 / xi +1)}}
qayerda z = x − m σ { displaystyle z = { frac {x- mu} { sigma}}} CDF 1 − ( 1 + ξ z ) − 1 / ξ { displaystyle 1- (1+ xi z) ^ {- 1 / xi} ,} Anglatadi m + σ 1 − ξ ( ξ < 1 ) { displaystyle mu + { frac { sigma} {1- xi}} , ; ( xi <1)} Median m + σ ( 2 ξ − 1 ) ξ { displaystyle mu + { frac { sigma (2 ^ { xi} -1)} { xi}}} Rejim Varians σ 2 ( 1 − ξ ) 2 ( 1 − 2 ξ ) ( ξ < 1 / 2 ) { displaystyle { frac { sigma ^ {2}} {(1- xi) ^ {2} (1-2 xi)}} , ; ( xi <1/2)} Noqulaylik 2 ( 1 + ξ ) 1 − 2 ξ ( 1 − 3 ξ ) ( ξ < 1 / 3 ) { displaystyle { frac {2 (1+ xi) { sqrt {1-2 xi}}} {(1-3 xi)}} , ; ( xi <1/3)} Ex. kurtoz 3 ( 1 − 2 ξ ) ( 2 ξ 2 + ξ + 3 ) ( 1 − 3 ξ ) ( 1 − 4 ξ ) − 3 ( ξ < 1 / 4 ) { displaystyle { frac {3 (1-2 xi) (2 xi ^ {2} + xi +3)} {{1-3 xi) (1-4 xi)}} - 3 , ; ( xi <1/4)} Entropiya jurnal ( σ ) + ξ + 1 { displaystyle log ( sigma) + xi +1} MGF e θ m ∑ j = 0 ∞ [ ( θ σ ) j ∏ k = 0 j ( 1 − k ξ ) ] , ( k ξ < 1 ) { displaystyle e ^ { theta mu} , sum _ {j = 0} ^ { infty} left [{ frac {( theta sigma) ^ {j}} { prod _ {k = 0} ^ {j} (1-k xi)}} o'ng], ; (k xi <1)} CF e men t m ∑ j = 0 ∞ [ ( men t σ ) j ∏ k = 0 j ( 1 − k ξ ) ] , ( k ξ < 1 ) { displaystyle e ^ {it mu} , sum _ {j = 0} ^ { infty} left [{ frac {(it sigma) ^ {j}} { prod _ {k = 0 } ^ {j} (1-k xi)}} o'ng], ; (k xi <1)} Lahzalar usuli ξ = 1 2 ( 1 − ( E [ X ] − m ) 2 V [ X ] ) { displaystyle xi = { frac {1} {2}} chap (1 - { frac {(E [X] - mu) ^ {2}} {V [X]}} o'ng)} σ = ( E [ X ] − m ) ( 1 − ξ ) { displaystyle sigma = (E [X] - mu) (1- xi)}
Yilda statistika , umumlashtirilgan Pareto taqsimoti (GPD) doimiy oiladir ehtimollik taqsimoti . Ko'pincha boshqa tarqatishning quyruqlarini modellashtirish uchun foydalaniladi. U uchta parametr bilan belgilanadi: joylashish m { displaystyle mu} σ { displaystyle sigma} ξ { displaystyle xi} [1] [2] [3] κ = − ξ { displaystyle kappa = - xi ,} [4]
Ta'rif
GPD ning standart kümülatif taqsimlash funktsiyasi (cdf) quyidagicha aniqlanadi[5]
F ξ ( z ) = { 1 − ( 1 + ξ z ) − 1 / ξ uchun ξ ≠ 0 , 1 − e − z uchun ξ = 0. { displaystyle F _ { xi} (z) = { begin {case} 1- chap (1+ xi z right) ^ {- 1 / xi} & { text {for}} xi neq 0, 1-e ^ {- z} & { text {for}} xi = 0. end {case}}} qo'llab-quvvatlash qaerda z ≥ 0 { displaystyle z geq 0} ξ ≥ 0 { displaystyle xi geq 0} 0 ≤ z ≤ − 1 / ξ { displaystyle 0 leq z leq -1 / xi} ξ < 0 { displaystyle xi <0}
f ξ ( z ) = { ( 1 + ξ z ) − ξ + 1 ξ uchun ξ ≠ 0 , e − z uchun ξ = 0. { displaystyle f _ { xi} (z) = { begin {case} (1+ xi z) ^ {- { frac { xi +1} { xi}}} & { text {for} } xi neq 0, e ^ {- z} & { text {for}} xi = 0. end {case}}} Xarakteristikasi
Tegishli joylashuv miqyosidagi tarqatish oilasi argumentni almashtirish orqali olinadi z tomonidan x − m σ { displaystyle { frac {x- mu} { sigma}}}
The kümülatif taqsimlash funktsiyasi ning X ∼ G P D. ( m , σ , ξ ) { displaystyle X sim GPD ( mu, sigma, xi)} m ∈ R { displaystyle mu in mathbb {R}} σ > 0 { displaystyle sigma> 0} ξ ∈ R { displaystyle xi in mathbb {R}}
F ( m , σ , ξ ) ( x ) = { 1 − ( 1 + ξ ( x − m ) σ ) − 1 / ξ uchun ξ ≠ 0 , 1 − tugatish ( − x − m σ ) uchun ξ = 0 , { displaystyle F _ {( mu, sigma, xi)} (x) = { begin {case} 1- left (1 + { frac { xi (x- mu)} {{sigma} } o'ng) ^ {- 1 / xi} & { text {for}} xi neq 0, 1- exp left (- { frac {x- mu} { sigma}} right) & { text {for}} xi = 0, end {case}}} qaerda qo'llab-quvvatlash X { displaystyle X} x ⩾ m { displaystyle x geqslant mu} ξ ⩾ 0 { displaystyle xi geqslant 0 ,} m ⩽ x ⩽ m − σ / ξ { displaystyle mu leqslant x leqslant mu - sigma / xi} ξ < 0 { displaystyle xi <0}
The ehtimollik zichligi funktsiyasi (pdf) ning X ∼ G P D. ( m , σ , ξ ) { displaystyle X sim GPD ( mu, sigma, xi)}
f ( m , σ , ξ ) ( x ) = 1 σ ( 1 + ξ ( x − m ) σ ) ( − 1 ξ − 1 ) { displaystyle f _ {( mu, sigma, xi)} (x) = { frac {1} { sigma}} chap (1 + { frac { xi (x- mu)}} sigma}} o'ng) ^ { chap (- { frac {1} { xi}} - 1 o'ng)}} yana, uchun x ⩾ m { displaystyle x geqslant mu} ξ ⩾ 0 { displaystyle xi geqslant 0} m ⩽ x ⩽ m − σ / ξ { displaystyle mu leqslant x leqslant mu - sigma / xi} ξ < 0 { displaystyle xi <0}
Pdf quyidagilarning echimi differentsial tenglama :[iqtibos kerak
{ f ′ ( x ) ( − m ξ + σ + ξ x ) + ( ξ + 1 ) f ( x ) = 0 , f ( 0 ) = ( 1 − m ξ σ ) − 1 ξ − 1 σ } { displaystyle left {{ begin {array} {l} f '(x) (- mu xi + sigma + xi x) + ( xi +1) f (x) = 0, f (0) = { frac { chap (1 - { frac { mu xi} { sigma}} o'ng) ^ {- { frac {1} { xi}} - 1}} { sigma}} end {array}} right }} Maxsus holatlar
Agar shakl bo'lsa ξ { displaystyle xi} m { displaystyle mu} eksponensial taqsimot . Shakli bilan ξ > 0 { displaystyle xi> 0} m = σ / ξ { displaystyle mu = sigma / xi} Pareto tarqatish o'lchov bilan x m = σ / ξ { displaystyle x_ {m} = sigma / xi} a = 1 / ξ { displaystyle alpha = 1 / xi} Agar X { displaystyle X} ∼ { displaystyle sim} G P D. { displaystyle GPD} ( { displaystyle (} m = 0 { displaystyle mu = 0} σ { displaystyle sigma} ξ { displaystyle xi} ) { displaystyle)} Y = jurnal ( X ) ∼ e x G P D. ( σ , ξ ) { displaystyle Y = log (X) sim exGPD ( sigma, xi)} [1] . (exGPD-ning ma'nosi yuqori darajadagi umumlashtirilgan Pareto taqsimoti .) GPD ga o'xshash Burr taqsimoti . Umumlashtirilgan Pareto tasodifiy o'zgaruvchilarini yaratish
GPD tasodifiy o'zgaruvchilarini yaratish Agar U bu bir xil taqsimlangan (0, 1] da, keyin
X = m + σ ( U − ξ − 1 ) ξ ∼ G P D. ( m , σ , ξ ≠ 0 ) { displaystyle X = mu + { frac { sigma (U ^ {- xi} -1)} { xi}} sim GPD ( mu, sigma, xi neq 0)} va
X = m − σ ln ( U ) ∼ G P D. ( m , σ , ξ = 0 ) . { displaystyle X = mu - sigma ln (U) sim GPD ( mu, sigma, xi = 0).} Ikkala formulalar ham CD ning teskari tomoni bilan olinadi.
Matlab Statistika asboblar qutisida "gprnd" buyrug'idan foydalanib, umumiy Pareto tasodifiy sonlarini hosil qilishingiz mumkin.
GPD eksponent-Gamma aralashmasi sifatida GPD tasodifiy o'zgaruvchisi eksponentli tasodifiy o'zgaruvchi sifatida ham ifodalanishi mumkin, Gamma taqsimlangan tezlik parametri.
X | Λ ∼ E x p ( Λ ) { displaystyle X | Lambda sim Exp ( Lambda)} va
Λ ∼ G a m m a ( a , β ) { displaystyle Lambda sim Gamma ( alfa, beta)} keyin
X ∼ G P D. ( ξ = 1 / a , σ = β / a ) { displaystyle X sim GPD ( xi = 1 / alfa, sigma = beta / alpha)} Ammo e'tibor bering, Gamma tarqatish parametrlari noldan katta bo'lishi kerak, biz qo'shimcha cheklovlarni olamiz: ξ { displaystyle xi}
Pareto-ning umumlashtirilgan taqsimoti
Yuqori darajadagi umumlashtirilgan Pareto taqsimoti (exGPD) Pdf
e x G P D. ( σ , ξ ) { displaystyle exGPD ( sigma, xi)} (turli darajadagi umumlashtirilgan Pareto taqsimoti)
σ { displaystyle sigma} va
ξ { displaystyle xi} .
Agar X ∼ G P D. { displaystyle X sim GPD} ( { displaystyle (} m = 0 { displaystyle mu = 0} σ { displaystyle sigma} ξ { displaystyle xi} ) { displaystyle)} Y = jurnal ( X ) { displaystyle Y = log (X)} yuqori darajadagi umumlashtirilgan Pareto taqsimoti Y { displaystyle Y} ∼ { displaystyle sim} e x G P D. { displaystyle exGPD} ( { displaystyle (} σ { displaystyle sigma} ξ { displaystyle xi} ) { displaystyle)}
The ehtimollik zichligi funktsiyasi (pdf) ning Y { displaystyle Y} ∼ { displaystyle sim} e x G P D. { displaystyle exGPD} ( { displaystyle (} σ { displaystyle sigma} ξ { displaystyle xi} ) ( σ > 0 ) { displaystyle) , , ( sigma> 0)}
g ( σ , ξ ) ( y ) = { e y σ ( 1 + ξ e y σ ) − 1 / ξ − 1 uchun ξ ≠ 0 , 1 σ e y − e y / σ uchun ξ = 0 , { displaystyle g _ {( sigma, xi)} (y) = { begin {case} { frac {e ^ {y}} { sigma}} { bigg (} 1 + { frac { xi e ^ {y}} { sigma}} { bigg)} ^ {- 1 / xi -1} , , , , { text {for}} xi neq 0, { frac {1} { sigma}} e ^ {ye ^ {y} / sigma} , , , , , , , , , , , , , , }, , , , , , , , , , , , , , , , , , , , { text {for}} xi = 0, tugatish {holatlar}}} qo'llab-quvvatlash qaerda − ∞ < y < ∞ { displaystyle - infty ξ ≥ 0 { displaystyle xi geq 0} − ∞ < y ≤ jurnal ( − σ / ξ ) { displaystyle - infty ξ < 0 { displaystyle xi <0}
Barcha uchun ξ { displaystyle xi} jurnal σ { displaystyle log sigma} ξ { displaystyle xi}
The exGPD barcha buyurtmalarning cheklangan daqiqalariga ega σ > 0 { displaystyle sigma> 0} − ∞ < ξ < ∞ { displaystyle - infty < xi < infty}
The
dispersiya ning
e x G P D. ( σ , ξ ) { displaystyle exGPD ( sigma, xi)} funktsiyasi sifatida
ξ { displaystyle xi} . Variant faqat bog'liqligiga e'tibor bering
ξ { displaystyle xi} . Nuqtali qizil chiziq baholangan dispersiyani anglatadi
ξ = 0 { displaystyle xi = 0} , anavi,
ψ ′ ( 1 ) = π 2 / 6 { displaystyle psi ^ {'} (1) = pi ^ {2} / 6} .
The moment hosil qiluvchi funktsiya ning Y ∼ e x G P D. ( σ , ξ ) { displaystyle Y sim exGPD ( sigma, xi)}
M Y ( s ) = E [ e s Y ] = { − 1 ξ ( − σ ξ ) s B ( s + 1 , − 1 / ξ ) uchun s ∈ ( − 1 , ∞ ) , ξ < 0 , 1 ξ ( σ ξ ) s B ( s + 1 , 1 / ξ − s ) uchun s ∈ ( − 1 , 1 / ξ ) , ξ > 0 , σ s Γ ( 1 + s ) uchun s ∈ ( − 1 , ∞ ) , ξ = 0 , { displaystyle M_ {Y} (s) = E [e ^ {sY}] = { begin {case} - { frac {1} { xi}} { bigg (} - { frac { sigma } { xi}} { bigg)} ^ {s} B (s + 1, -1 / xi) , , , , , , , , , , , , , { text {for}} s in (-1, infty), xi <0, { frac {1} { xi}} { bigg (} { frac { sigma} { xi}} { bigg)} ^ {s} B (s + 1,1 / xi -s) , , , , , , , , , , , , , , , , , , { text {for}} s in (-1,1 / xi), xi> 0, sigma ^ {s} Gamma (1 + s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} s in (-1, infty), xi = 0, end {case}}} qayerda B ( a , b ) { displaystyle B (a, b)} Γ ( a ) { displaystyle Gamma (a)} beta funktsiyasi va gamma funktsiyasi navbati bilan.
The kutilayotgan qiymat ning Y { displaystyle Y} ∼ { displaystyle sim} e x G P D. { displaystyle exGPD} ( { displaystyle (} σ { displaystyle sigma} ξ { displaystyle xi} ) { displaystyle)} σ { displaystyle sigma} ξ { displaystyle xi} ξ { displaystyle xi} digamma funktsiyasi :
E [ Y ] = { jurnal ( − σ ξ ) + ψ ( 1 ) − ψ ( − 1 / ξ + 1 ) uchun ξ < 0 , jurnal ( σ ξ ) + ψ ( 1 ) − ψ ( 1 / ξ ) uchun ξ > 0 , jurnal σ + ψ ( 1 ) uchun ξ = 0. { displaystyle E [Y] = { begin {case} log { bigg (} - { frac { sigma} { xi}} { bigg)} + psi (1) - psi ( -1 / xi +1) , , , , , , , , , , , , , , , , { text {for}} xi <0, log { bigg (} { frac { sigma} { xi}} { bigg)} + psi (1) - psi (1 / xi) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi> 0, log sigma + psi (1) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , {, text {for}} xi = 0. end {case}}} Uchun belgilangan qiymat uchun ekanligini unutmang ξ ∈ ( − ∞ , ∞ ) { displaystyle xi in (- infty, infty)} jurnal σ { displaystyle log sigma}
The dispersiya ning Y { displaystyle Y} ∼ { displaystyle sim} e x G P D. { displaystyle exGPD} ( { displaystyle (} σ { displaystyle sigma} ξ { displaystyle xi} ) { displaystyle)} ξ { displaystyle xi} poligamma funktsiyasi buyurtmaning 1 (shuningdek, trigamma funktsiyasi ):
V a r [ Y ] = { ψ ′ ( 1 ) − ψ ′ ( − 1 / ξ + 1 ) uchun ξ < 0 , ψ ′ ( 1 ) + ψ ′ ( 1 / ξ ) uchun ξ > 0 , ψ ′ ( 1 ) uchun ξ = 0. { displaystyle Var [Y] = { begin {case} psi ^ {'} (1) - psi ^ {'} (- 1 / xi +1) , , , , , , , , , , , , , , { text {for}} xi <0, psi ^ {'} (1) + psi ^ {'} (1 / xi ) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi> 0, psi ^ {'} (1) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi = 0. end {case}}} Funksiya sifatida dispersiya uchun o'ng panelga qarang ξ { displaystyle xi} ψ ′ ( 1 ) = π 2 / 6 ≈ 1.644934 { displaystyle psi ^ {'} (1) = pi ^ {2} / 6 taxminan 1.644934}
Shkala parametrining rollariga e'tibor bering σ { displaystyle sigma} ξ { displaystyle xi} Y ∼ e x G P D. ( σ , ξ ) { displaystyle Y sim exGPD ( sigma, xi)} ξ { displaystyle xi} X ∼ G P D. ( σ , ξ ) { displaystyle X sim GPD ( sigma, xi)} [2] . Ikkala parametrning rollari bir-biriga bog'liqdir X ∼ G P D. ( m = 0 , σ , ξ ) { displaystyle X sim GPD ( mu = 0, sigma, xi)} V a r ( X ) { displaystyle Var (X)}
Tepalikning taxminchisi
Buni taxmin qiling X 1 : n = ( X 1 , ⋯ , X n ) { displaystyle X_ {1: n} = (X_ {1}, cdots, X_ {n})} n { displaystyle n} og'ir dumaloq taqsimot F { displaystyle F} 1 / ξ { displaystyle 1 / xi} ξ { displaystyle xi}
F ¯ ( x ) = 1 − F ( x ) = L ( x ) ⋅ x − 1 / ξ , kimdir uchun ξ > 0 , qayerda L asta-sekin o'zgarib turadigan funktsiya. { displaystyle { bar {F}} (x) = 1-F (x) = L (x) cdot x ^ {- 1 / xi}, , , , , , { text {ba'zi uchun}} xi> 0, , , { text {qaerda}} L { text {sekin o'zgaruvchan funktsiya.}}} Bu alohida qiziqish uyg'otadi haddan tashqari qiymat nazariyasi shakl parametrini baholash uchun ξ { displaystyle xi} ξ { displaystyle xi}
Ruxsat bering F siz { displaystyle F_ {u}} Pikandlar – Balkema – de Haan teoremasi (Pickands, 1975; Balkema va de Haan, 1974) ta'kidlashicha, asosiy tarqatish funktsiyalarining katta klassi uchun F { displaystyle F} siz { displaystyle u} F siz { displaystyle F_ {u}} ξ { displaystyle xi} GPD POT yondashuvida asosiy rol o'ynaydi.
POT metodologiyasidan foydalangan taniqli tahminchi bu Tepaning taxminchisi . Tepalikni taxmin qilish texnik tavsifi quyidagicha. Uchun 1 ≤ men ≤ n { displaystyle 1 leq i leq n} X ( men ) { displaystyle X _ {(i)}} men { displaystyle i} X 1 , ⋯ , X n { displaystyle X_ {1}, cdots, X_ {n}} Tepaning taxminchisi (Embrechts va boshqalarning 5-ma'lumotnomasining 190-betiga qarang [3] ) ga asoslangan k { displaystyle k}
ξ ^ k Tepalik = ξ ^ k Tepalik ( X 1 : n ) = 1 k − 1 ∑ j = 1 k − 1 jurnal ( X ( j ) X ( k ) ) , uchun 2 ≤ k ≤ n . { displaystyle { widehat { xi}} _ {k} ^ { text {Hill}} = { widehat { xi}} _ {k} ^ { text {Hill}} (X_ {1: n) }) = { frac {1} {k-1}} sum _ {j = 1} ^ {k-1} log { bigg (} { frac {X _ {(j)}} {X_ { (k)}}} { bigg)}, , , , , , , , , {, text {for}}} 2 leq k leq n.} Amalda Tepalik tahmini quyidagicha qo'llaniladi. Birinchidan, taxmin qiluvchini hisoblang ξ ^ k Tepalik { displaystyle { widehat { xi}} _ {k} ^ { text {Hill}}} k ∈ { 2 , ⋯ , n } { displaystyle k in {2, cdots, n }} { ( k , ξ ^ k Tepalik ) } k = 2 n { displaystyle {(k, { widehat { xi}} _ {k} ^ { text {Hill}}) } _ {k = 2} ^ {n}} { ξ ^ k Tepalik } k = 2 n { displaystyle {{ widehat { xi}} _ {k} ^ { text {Hill}} } _ {k = 2} ^ {n}} k { displaystyle k} ξ { displaystyle xi} X 1 , ⋯ , X n { displaystyle X_ {1}, cdots, X_ {n}} ξ { displaystyle xi} [4] .
E'tibor bering Tepalik tahmini ξ ^ k Tepalik { displaystyle { widehat { xi}} _ {k} ^ { text {Hill}}} X 1 : n = ( X 1 , ⋯ , X n ) { displaystyle X_ {1: n} = (X_ {1}, cdots, X_ {n})} Pikandning taxminchisi ξ ^ k Pickand { displaystyle { widehat { xi}} _ {k} ^ { text {Pickand}}} [5] .)
Shuningdek qarang
Adabiyotlar
Qo'shimcha o'qish
Pikands, Jeyms (1975). "Haddan tashqari buyurtma statistikasi yordamida statistik xulosa" . Statistika yilnomalari . 3 s : 119–131. doi :10.1214 / aos / 1176343003 Balkema, A .; De Xaan, Lorens (1974). "Katta yoshdagi qoldiq hayot vaqti" . Ehtimollar yilnomasi . 2 (5): 792–804. doi :10.1214 / aop / 1176996548 Li, Seyun; Kim, J.X.K. (2018). "Yuqori darajadagi umumlashtirilgan Pareto taqsimoti: ekstremal qiymat nazariyasi xususiyatlari va ilovalari". Statistikadagi aloqa - nazariya va usullar . 0 (8): 1–25. arXiv :1708.01686 doi :10.1080/03610926.2018.1441418 . S2CID 88514574 . N. L. Jonson; S. Kotz; N. Balakrishnan (1994). Uzluksiz o'zgaruvchan tarqatish 1-jild, ikkinchi nashr . Nyu-York: Vili. ISBN 978-0-471-58495-7 Barri C. Arnold (2011). "7-bob: Pareto va umumiy paretoning tarqatilishi" . Duangkamon Chotikapanichda (tahr.). Modellashtirish taqsimotlari va Lorenz egri chiziqlari . Nyu-York: Springer. ISBN 9780387727967 Arnold, B. C .; Laguna, L. (1977). Daromad ma'lumotlariga arizalar bilan umumiy Pareto tarqatish to'g'risida . Ames, Ayova: Ayova shtati universiteti, iqtisodiy bo'lim. Tashqi havolalar
Diskret o'zgaruvchan Diskret o'zgaruvchan Doimiy o'zgaruvchan Doimiy o'zgaruvchan Doimiy o'zgaruvchan Doimiy o'zgaruvchan Aralashtirilgan uzluksiz diskret bir o'zgaruvchidir Ko'p o'zgaruvchan (qo'shma) Yo'naltirilgan Degeneratsiya va yakka Oilalar


















![{ displaystyle e ^ { theta mu} , sum _ {j = 0} ^ { infty} left [{ frac {( theta sigma) ^ {j}} { prod _ {k = 0} ^ {j} (1-k xi)}} o'ng], ; (k xi <1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cf9f358ac58dcba4130cba492879256576e783)
![{ displaystyle e ^ {it mu} , sum _ {j = 0} ^ { infty} left [{ frac {(it sigma) ^ {j}} { prod _ {k = 0 } ^ {j} (1-k xi)}} o'ng], ; (k xi <1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53bfef161abce3834ebc5908620389e3174d612f)
![{ displaystyle xi = { frac {1} {2}} chap (1 - { frac {(E [X] - mu) ^ {2}} {V [X]}} o'ng)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/029894dab6a61a875e17d8ee5f27c7fe52dc4a89)
![{ displaystyle sigma = (E [X] - mu) (1- xi)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae5aff7c32202ca44e85df4abac26bc3e6deb14)


















































![{ displaystyle M_ {Y} (s) = E [e ^ {sY}] = { begin {case} - { frac {1} { xi}} { bigg (} - { frac { sigma } { xi}} { bigg)} ^ {s} B (s + 1, -1 / xi) , , , , , , , , , , , , , { text {for}} s in (-1, infty), xi <0, { frac {1} { xi}} { bigg (} { frac { sigma} { xi}} { bigg)} ^ {s} B (s + 1,1 / xi -s) , , , , , , , , , , , , , , , , , , { text {for}} s in (-1,1 / xi), xi> 0, sigma ^ {s} Gamma (1 + s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} s in (-1, infty), xi = 0, end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28884f7453a08deb806e6dcfadd72715427ba40b)


![{ displaystyle E [Y] = { begin {case} log { bigg (} - { frac { sigma} { xi}} { bigg)} + psi (1) - psi ( -1 / xi +1) , , , , , , , , , , , , , , , , { text {for}} xi <0, log { bigg (} { frac { sigma} { xi}} { bigg)} + psi (1) - psi (1 / xi) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi> 0, log sigma + psi (1) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , {, text {for}} xi = 0. end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8417be06df13f42af281e304598ef2e687d03b5)


![{ displaystyle Var [Y] = { begin {case} psi ^ {'} (1) - psi ^ {'} (- 1 / xi +1) , , , , , , , , , , , , , , { text {for}} xi <0, psi ^ {'} (1) + psi ^ {'} (1 / xi ) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi> 0, psi ^ {'} (1) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , { text {for}} xi = 0. end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc2be71c610d979bd9344ee0f3a460e61f750ce1)





















