WikiDer > To'g'ri taqsimlangan umumiy taqsimot

Ushbu maqola umumiy ro'yxatini o'z ichiga oladi ma'lumotnomalar, lekin bu asosan tasdiqlanmagan bo'lib qolmoqda, chunki unga mos keladigan etishmayapti satrda keltirilgan. Iltimos yordam bering yaxshilash tomonidan ushbu maqola tanishtirish aniqroq iqtiboslar. (2015 yil sentyabr) (Ushbu shablon xabarini qanday va qachon olib tashlashni bilib oling)

Yilda ehtimollik va statistika, qiyshiq umumlashtirilgan "t" taqsimoti doimiy oiladir ehtimollik taqsimoti. Tarqatish birinchi bo'lib Panayiotis Theodossiou tomonidan kiritilgan^[1] 1998 yilda. Tarqatish shu vaqtdan beri turli xil qo'llanmalarda ishlatilgan.^{[2][3][4][5][6][7]} Eğimli umumlashtirilgan t tarqatish uchun turli xil parametrlar mavjud.^[1][5]

Ta'rif

Ehtimollar zichligi funktsiyasi

${ displaystyle f_ {SGT} (x; mu, sigma, lambda, p, q) = { frac {p} {2v sigma q ^ {1 / p} B ({ frac {1} {) p}}, q) chap ({ frac {| x- mu + m | ^ {p}} {q (v sigma) ^ {p} ( lambda belgisi (x- mu + m) + 1) ^ {p}}} + 1 o'ng) ^ {{ frac {1} {p}} + q}}}}$

qayerda ${ displaystyle B}$ bo'ladi beta funktsiyasi, ${ displaystyle mu}$ joylashuv parametri, ${ displaystyle sigma> 0}$ o'lchov parametri, ${ displaystyle -1 < lambda <1}$ skewness parametri va ${ displaystyle p> 0}$ va ${ displaystyle q> 0}$ kurtozni boshqaradigan parametrlardir. ${ displaystyle m}$ va ${ displaystyle v}$ parametrlar emas, balki bu taqsimotning turli parametrlariga mos kelish uchun taqsimotni mos ravishda siljitish yoki siljitish uchun ishlatiladigan boshqa parametrlarning funktsiyalari.

Asl parametrlashda^[1] qiyshiq umumlashtirilgan t taqsimotining,

${ displaystyle m = { frac {2v sigma lambda q ^ { frac {1} {p}} B ({ frac {2} {p}}, q - { frac {1} {p} })} {B ({ frac {1} {p}}, q)}}}$

va

${ displaystyle v = { frac {q ^ {- { frac {1} {p}}}} { sqrt {(3 lambda ^ {2} +1) { frac {B ({ frac {) 3} {p}}, q - { frac {2} {p}})} {B ({ frac {1} {p}}, q)}} - 4 lambda ^ {2} { frac {B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ {2}} {B ({ frac {1} {p}}, q) ^ { 2}}}}}}}$.

Ushbu qiymatlar ${ displaystyle m}$ va ${ displaystyle v}$ ning taqsimotini o'rtacha ${ displaystyle mu}$ agar ${ displaystyle pq> 1}$ va dispersiyasi ${ displaystyle sigma ^ {2}}$ agar ${ displaystyle pq> 2}$. Buning uchun ${ displaystyle m}$ ammo bu qiymatga ega bo'lish uchun shunday bo'lishi kerak ${ displaystyle pq> 1}$. Xuddi shunday, uchun ${ displaystyle v}$ yuqoridagi qiymatga tenglashtirish uchun, ${ displaystyle pq> 2}$.

Ehtimollik zichligi funktsiyasining eng oddiy funktsional shaklini beradigan parametrlash ${ displaystyle m = 0}$ va ${ displaystyle v = 1}$. Bu degani

${ displaystyle mu + { frac {2v sigma lambda q ^ { frac {1} {p}} B ({ frac {2} {p}}, q - { frac {1} {p }})} {B ({ frac {1} {p}}, q)}}}$

va dispersiyasi

${ displaystyle sigma ^ {2} q ^ { frac {2} {p}} ((3 lambda ^ {2} +1) { frac {B ({ frac {3} {p}}, q - { frac {2} {p}})} {B ({ frac {1} {p}}, q)}} - 4 lambda ^ {2} { frac {B ({ frac {) 2} {p}}, q - { frac {1} {p}}) ^ {2}} {B ({ frac {1} {p}}, q) ^ {2}}})}$

The ${ displaystyle lambda}$ parametr taqsimotning egriligini boshqaradi. Buni ko'rish uchun ruxsat bering ${ displaystyle M}$ tarqatish rejimini belgilang va

${ displaystyle int _ {- infty} ^ {M} f_ {SGT} (x; mu, sigma, lambda, p, q) dx = { frac {1- lambda} {2}} }$

Beri ${ displaystyle -1 < lambda <1}$, rejimdan chapdagi ehtimollik, shuning uchun rejimning o'ng tomoni ham qiymatiga qarab (0,1) da istalgan qiymatga teng bo'lishi mumkin ${ displaystyle lambda}$. Shunday qilib, qiyshiq umumlashtirilgan t taqsimot nosimmetrik kabi yuqori darajada qiyshayishi mumkin. Agar ${ displaystyle -1 < lambda <0}$, keyin tarqatish salbiy tomonga buriladi. Agar ${ displaystyle 0 < lambda <1}$, keyin tarqatish ijobiy tomonga buriladi. Agar ${ displaystyle lambda = 0}$, keyin taqsimot nosimmetrikdir.

Nihoyat, ${ displaystyle p}$ va ${ displaystyle q}$ tarqatish kurtozini nazorat qilish. Sifatida ${ displaystyle p}$ va ${ displaystyle q}$ kichrayib, kurtoz kuchayadi^[1] (ya'ni leptokurtikaga aylanadi). Ning katta qiymatlari ${ displaystyle p}$ va ${ displaystyle q}$ platikurtik bo'lgan taqsimot hosil qiling.

Lahzalar

Ruxsat bering ${ displaystyle X}$ qiyshiq umumlashtirilgan t taqsimot bilan taqsimlangan tasodifiy o'zgaruvchi bo'ling. The ${ displaystyle h ^ {th}}$ lahza (ya'ni ${ displaystyle E [(X-E (X)) ^ {h}]}$), uchun ${ displaystyle pq> h}$, bu:${ displaystyle sum _ {r = 0} ^ {h} { binom {h} {r}} ((1+ lambda) ^ {r + 1} + (- 1) ^ {r} (1-) lambda) ^ {r + 1}) (- lambda) ^ {hr} { frac {(v sigma) ^ {h} q ^ { frac {h} {p}} B ({ frac {) r + 1} {p}}, q - { frac {r} {p}}) B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ { hr}} {2 ^ {r-h + 1} B ({ frac {1} {p}}, q) ^ {h-r + 1}}}}$

O'rtacha, chunki ${ displaystyle pq> 1}$, bu:

${ displaystyle mu + { frac {2v sigma lambda q ^ { frac {1} {p}} B ({ frac {2} {p}}, q - { frac {1} {p }})} {B ({ frac {1} {p}}, q)}} - m}$

Variant (ya'ni ${ displaystyle E [(X-E (X)) ^ {2}]}$), uchun ${ displaystyle pq> 2}$, bu:

${ displaystyle (v sigma) ^ {2} q ^ { frac {2} {p}} ((3 lambda ^ {2} +1) { frac {B ({ frac {3} {p) }}, q - { frac {2} {p}})} {B ({ frac {1} {p}}, q)}} - 4 lambda ^ {2} { frac {B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ {2}} {B ({ frac {1} {p}}, q) ^ {2}}} )}$

Noqulaylik (ya'ni ${ displaystyle E [(X-E (X)) ^ {3}]}$), uchun ${ displaystyle pq> 3}$, bu:

${ displaystyle { frac {2q ^ {3 / p} lambda (v sigma) ^ {3}} {B ({ frac {1} {p}}, q) ^ {3}}} { Bigg (} 8 lambda ^ {2} B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ {3} -3 (1 + 3 lambda ^ { 2}) B ({ frac {1} {p}}, q)}$

${ displaystyle times B ({ frac {2} {p}}, q - { frac {1} {p}}) B ({ frac {3} {p}}, q - { frac { 2} {p}}) + 2 (1+ lambda ^ {2}) B ({ frac {1} {p}}, q) ^ {2} B ({ frac {4} {p}} , q - { frac {3} {p}}) { Bigg)}}$

Kurtoz (ya'ni ${ displaystyle E [(X-E (X)) ^ {4}]}$), uchun ${ displaystyle pq> 4}$, bu:

${ displaystyle { frac {q ^ {4 / p} (v sigma) ^ {4}} {B ({ frac {1} {p}}, q) ^ {4}}} { Bigg ( } -48 lambda ^ {4} B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ {4} +24 lambda ^ {2} (1+) 3 lambda ^ {2}) B ({ frac {1} {p}}, q) B ({ frac {2} {p}}, q - { frac {1} {p}}) ^ {2}}$

${ displaystyle marta B ({ frac {3} {p}}, q - { frac {2} {p}}) - 32 lambda ^ {2} (1+ lambda ^ {2}) B ({ frac {1} {p}}, q) ^ {2} B ({ frac {2} {p}}, q - { frac {1} {p}}) B ({ frac {) 4} {p}}, q - { frac {3} {p}})}$

${ displaystyle + (1 + 10 lambda ^ {2} +5 lambda ^ {4}) B ({ frac {1} {p}}, q) ^ {3} B ({ frac {5}) {p}}, q - { frac {4} {p}}) { Bigg)}}$

Maxsus ishlar

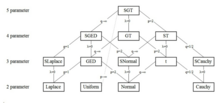
Eğimli umumlashtirilgan t taqsimotining maxsus va cheklovchi holatlariga, skandallangan umumlashtirilgan xato taqsimoti, McDonald va Newey tomonidan kiritilgan umumiy taqsimot,^[6] Hansen tomonidan taklif qilingan qiyshiq t,^[8] qiyshaygan Laplas taqsimoti, umumlashtirilgan xato taqsimoti ( umumlashtirilgan normal taqsimot), oddiy taqsimot, talaba tarqatish, qiyshiq Koshi taqsimoti, the Laplas taqsimoti, bir xil taqsimlash, normal taqsimot, va Koshi taqsimoti. Quyidagi grafik Hansen, McDonald va Neweydan moslashtirilgan,^[2] qiyshiq umumlashtirilgan t taqsimotining har xil maxsus qiymatlarini olish uchun qaysi parametrlarni o'rnatish kerakligini ko'rsatadi.

Eğimli umumlashtirilgan t tarqatish daraxti

Noto'g'ri umumlashtirilgan xato taqsimoti

Skewed Generalized Distribution-da pdf mavjud:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda, p, q)}$

${ displaystyle = f_ {SGED} (x; mu, sigma, lambda, p) = { frac {pe ^ {- ({ frac {| x- mu + m |} {v sigma ( 1+ lambda belgisi (x- mu + m))}}) ^ {p}}} {2v sigma Gamma (1 / p)}}}$

qayerda

${ displaystyle m = { frac {2 ^ { frac {2} {p}} v sigma lambda Gamma ({ frac {1} {2}} + { frac {1} {p}} )} { sqrt { pi}}}}$

degan ma'noni anglatadi ${ displaystyle mu}$. Shuningdek

${ displaystyle v = { sqrt { frac { pi Gamma ({ frac {1} {p}})} { pi (1 + 3 lambda ^ {2}) Gamma ({ frac { 3} {p}}) - 16 ^ { frac {1} {p}} lambda ^ {2} Gamma ({ frac {1} {2}} + { frac {1} {p}} ) ^ {2} Gamma ({ frac {1} {p}})}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Umumlashtirilgan t taqsimoti

Umumlashtirilgan T taqsimotida pdf mavjud:

${ displaystyle f_ {SGT} (x; mu, sigma, lambda = 0, p, q)}$

${ displaystyle = f_ {GT} (x; mu, sigma, p, q) = { frac {p} {2v sigma q ^ {1 / p} B ({ frac {1} {p}) }, q) ({ frac { left | x- mu right | ^ {p}} {q (v sigma) ^ {p}}} + 1) ^ {{ frac {1} {p }} + q}}}}$

qayerda

${ displaystyle v = { frac {1} {q ^ {1 / p}}} { sqrt { frac {B ({ frac {1} {p}}, q)} {B ({ frac) {3} {p}}, q - { frac {2} {p}})}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

To'g'ri taqsimlash

Skewed T Distribution pdf-ga ega:

${ displaystyle f_ {SGT} (x; mu, sigma, lambda, p = 2, q)}$

${ displaystyle = f_ {ST} (x; mu, sigma, lambda, q) = { frac { Gamma ({ frac {1} {2}} + q)} {v sigma ( pi q) ^ {1/2} Gamma (q) ({ frac { left | x- mu + m right | ^ {2}} {q (v sigma) ^ {2} ( lambda) ~ { rm {sign}} (x- mu + m) +1) ^ {2}}} + 1) ^ {{ frac {1} {2}} + q}}}}$

qayerda

${ displaystyle m = { frac {2v sigma lambda q ^ {1/2} Gamma (q - { frac {1} {2}})} { pi ^ {1/2} Gamma ( q)}}}$

degan ma'noni anglatadi ${ displaystyle mu}$. Shuningdek

${ displaystyle v = { frac {1} {q ^ {1/2} { sqrt {(3 lambda ^ {2} +1) ({ frac {1} {2q-2}}) - { frac {4 lambda ^ {2}} { pi}} chap ({ frac { Gamma (q - { frac {1} {2}})} { Gamma (q)}} o'ng ) {{2}}}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Laplasning taqsimlanishi

Skaped Laplace Distribution pdf-ga ega:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda, p = 1, q)}$

${ displaystyle = f_ {SLaplace} (x; mu, sigma, lambda) = { frac {e ^ { frac {- | x- mu + m |} {v sigma (1+ lambda) belgisi (x- mu + m))}}} {2v sigma}}}$

qayerda

${ displaystyle m = 2v sigma lambda}$

degan ma'noni anglatadi ${ displaystyle mu}$. Shuningdek

${ displaystyle v = [2 (1+ lambda ^ {2})] ^ {- { frac {1} {2}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Umumiy xatolarni taqsimlash

Umumiy xatolarni tarqatish (shuningdek, umumlashtirilgan normal taqsimot) pdf-ga ega:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda = 0, p, q)}$

${ displaystyle = f_ {GED} (x; mu, sigma, p) = { frac {pe ^ {- ({ frac {| x- mu |} {v sigma}}) ^ {p }}} {2v sigma Gamma (1 / p)}}}$

qayerda

${ displaystyle v = { sqrt { frac { Gamma ({ frac {1} {p}})} { Gamma ({ frac {3} {p}})}}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Oddiy taqsimot

Skewed Normal Distribution pdf-ga ega:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda, p = 2, q)}$

${ displaystyle = f_ {SNormal} (x; mu, sigma, lambda) = { frac {e ^ {- ({ frac {| x- mu + m |} {v sigma (1+) lambda belgisi (x- mu + m))}}) ^ {2}}} {v sigma { sqrt { pi}}}}}$

qayerda

${ displaystyle m = { frac {2v sigma lambda} { sqrt { pi}}}}$

degan ma'noni anglatadi ${ displaystyle mu}$. Shuningdek

${ displaystyle v = { sqrt { frac {2 pi} {( pi -8 lambda ^ {2} +3 pi lambda ^ {2})}}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Talabalarning t-taqsimoti

The Talabalarning t-taqsimoti pdf-ga ega:

${ displaystyle f_ {SGT} (x; mu = 0, sigma = 1, lambda = 0, p = 2, q = d / 2)}$

${ displaystyle = f_ {T} (x; d) = { frac { Gamma ({ frac {d + 1} {2}})} {( pi d) ^ {1/2} Gamma ( d / 2) ({ frac {x ^ {2}} {d}} + 1) ^ { frac {d + 1} {2}}}}}$

${ displaystyle v = { sqrt {2}}}$ almashtirildi.

Qo'shma Koshi taqsimoti

Skewed Cauchy Distribution pdf-ga ega:

${ displaystyle f_ {SGT} (x; mu, sigma, lambda, p = 2, q = 1/2)}$

${ displaystyle = f_ {SCauchy} (x; mu, sigma, lambda) = { frac {1} { sigma pi ({ frac { left | x- mu right | ^ {2 }} { sigma ^ {2} ( lambda belgisi (x- mu) +1) ^ {2}}} + 1)}}}$

${ displaystyle v = { sqrt {2}}}$ va ${ displaystyle m = 0}$ almashtirildi.

Eğimli Koshi tarqalishining o'rtacha, dispersiyasi, qiyshiqligi va kurtozi aniqlanmagan.

Laplas taqsimoti

The Laplas taqsimoti pdf-ga ega:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda = 0, p = 1, q)}$

${ displaystyle = f_ {Laplace} (x; mu, sigma) = { frac {e ^ { frac {- | x- mu |} { sigma}}} {2 sigma}}}$

${ displaystyle v = 1}$ almashtirildi.

Yagona tarqatish

The Yagona tarqatish pdf-ga ega:

${ displaystyle lim _ {p to infty} f_ {SGT} (x; mu, sigma, lambda, p, q)}$

${ displaystyle = f (x) = { begin {case} { frac {1} {2v sigma}} & | x- mu |$

Shunday qilib standart bir xil parametrlash olinadi, agar ${ displaystyle mu = { frac {a + b} {2}}}$, ${ displaystyle v = 1}$va ${ displaystyle sigma = { frac {b-a} {2}}}$.

Oddiy taqsimot

The Oddiy taqsimot pdf-ga ega:

${ displaystyle lim _ {q to infty} f_ {SGT} (x; mu, sigma, lambda = 0, p = 2, q)}$

${ displaystyle = f_ {Normal} (x; mu, sigma) = { frac {e ^ {- ({ frac {| x- mu |} {v sigma}}) ^ {2}} } {v sigma { sqrt { pi}}}}}$

qayerda

${ displaystyle v = { sqrt {2}}}$

ning dispersiyasini beradi ${ displaystyle sigma ^ {2}}$.

Cauchy Distribution

The Koshi taqsimoti pdf-ga ega:

${ displaystyle f_ {SGT} (x; mu, sigma, lambda = 0, p = 2, q = 1/2)}$

${ displaystyle = f_ {Cauchy} (x; mu, sigma) = { frac {1} { sigma pi (({ frac {x- mu} { sigma}}) ^ {2} +1)}}}$

${ displaystyle v = { sqrt {2}}}$ almashtirildi.

Adabiyotlar

• Hansen, B. (1994). "Avtoregressiv shartli zichlikni baholash". Xalqaro iqtisodiy sharh. 35 (3): 705–730. doi:10.2307/2527081. JSTOR 2527081.
• Xansen, C .; Makdonald, J .; Newey, W. (2010). "Moslashuvchan taqsimot bilan instrumental o'zgaruvchilarni baholash". Biznes va iqtisodiy statistika jurnali. 28: 13–25. doi:10.1198 / jbes.2009.06161. hdl:10419/79273.
• Xansen, C .; Makdonald, J .; Theodossiou, P. (2007). "Ekonometrik modellarning qisman moslashuvchan baholovchilari uchun moslashuvchan parametrli modellar". Iqtisodiyot: Open-Access, Open-Assessment elektron jurnali. 1 (2007–7): 1. doi:10.5018 / Economics-ejournal.ja.2007-7.
• Makdonald, J .; Mikhefelder, R .; Theodossiou, P. (2009). "Sog'lom regressiyani baholash usullarini baholash va to'sib qo'yilgan noaniqlik: kapital aktivlariga narxlarni aniqlash modelini qo'llash" (PDF). Ko'p millatli moliya jurnali. 15 (3/4): 293–321. doi:10.17578/13-3/4-6.
• Makdonald, J .; Mishelfelder, R .; Theodossiou, P. (2010). "Moslashuvchan parametrlarni taqsimlash bilan ishonchli baholash: foydali fond betalarini baholash". Miqdoriy moliya. 10 (4): 375–387. doi:10.1080/14697680902814241.
• Makdonald, J .; Newey, W. (1988). "Regressiya modellarini qisman adaptiv ravishda umumiy t taqsimot orqali baholash". Ekonometrik nazariya. 4 (3): 428–457. doi:10.1017 / s0266466600013384.
• Savva, C .; Theodossiou, P. (2015). "Skewness va xavf bilan qaytarish o'rtasidagi bog'liqlik". Menejment fanlari.
• Theodossiou, P. (1998). "Moliyaviy ma'lumotlar va qiyshiq umumlashtirilgan T tarqatish". Menejment fanlari. 44 (12-qism – 1): 1650–1661. doi:10.1287 / mnsc.44.12.1650.

Tashqi havolalar

• qiyshiq umumlashtirilgan t taqsimotini, uning maxsus holatlarini va uning pdf, cdf va muhim qiymatlarini hisoblash dasturini aks ettiradi

Izohlar